Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
48. Модель дуополии по Курно.Предположим, что две фирмы, A и B, производят аналогичный продукт. Обозначим через 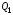 и и 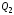 объёмы выпуска продукции соответственно фирмами A и B. Пусть объёмы выпуска продукции соответственно фирмами A и B. Пусть 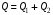 – совокупный объём выпуска продукции фирмами. Поскольку мы рассматриваем ситуацию дуополии, величина Q характеризует объём предложения на рынке. – совокупный объём выпуска продукции фирмами. Поскольку мы рассматриваем ситуацию дуополии, величина Q характеризует объём предложения на рынке.Для описания зависимости цены единицы продукции от величины предложения на рынке воспользуемся функцией 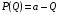 , ,  , если , если 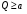 . Параметр a имеет смысл цены единицы продукции в случае, если . Параметр a имеет смысл цены единицы продукции в случае, если 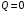 . .Для описания зависимости затрат на создание единицы продукции от масштаба производства введём в модель функции затрат 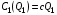 , , 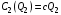 фирм. Функция отражает факт равенства предельных затрат (параметр c) на производство единицы продукции для рассматриваемых фирм A и B. фирм. Функция отражает факт равенства предельных затрат (параметр c) на производство единицы продукции для рассматриваемых фирм A и B.Обозначим множества стратегий фирм символами 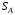 и и 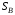 . Стратегии фирм заключаются в выборе определённого объёма выпуска продукции . Стратегии фирм заключаются в выборе определённого объёма выпуска продукции 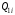 и и 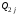 , т.е. , т.е. 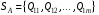 , , 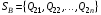 . Будем предполагать, что фирмы выбирают свои стратегии одновременно и независимо. Соответствующая данной игре матрица игровых ситуаций будем иметь вид: . Будем предполагать, что фирмы выбирают свои стратегии одновременно и независимо. Соответствующая данной игре матрица игровых ситуаций будем иметь вид: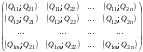 . .Выигрыши фирм в этой игре – их прибыли на рынке. Для расчёта прибылей фирм воспользуемся формулой: 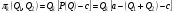 , , 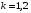 . .Каждая из фирм заинтересована в максимизации своей прибыли и каждая вынуждена учитывать интересы своего конкурента. Возникает вопрос, существует ли пара стратегий фирм 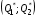 , от которых ни одной из них не выгодно отклониться. Существуют ли оптимальные объёмы выпуска фирм, оптимальные и учитывающие интересы конкурентов. Другими словами, существует ли равновесие Нэша в данной игре? Проверим это. , от которых ни одной из них не выгодно отклониться. Существуют ли оптимальные объёмы выпуска фирм, оптимальные и учитывающие интересы конкурентов. Другими словами, существует ли равновесие Нэша в данной игре? Проверим это.Если пара 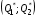 существует, то для её поиска фирмы решают следующие задачи: существует, то для её поиска фирмы решают следующие задачи: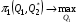 , , 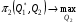 . .Решим задачу максимизации прибыли для фирмы A. 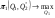 . .Воспользуемся необходимым условием существования экстремума. 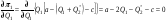 Получаем, что 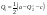 . .Для фирмы B: 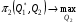 , ,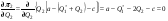 , ,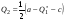 . .Можно показать, что полученные выражения 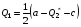 и и 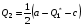 определяют объёмы выпуска, доставляющие максимумы функциям прибыли определяют объёмы выпуска, доставляющие максимумы функциям прибыли 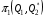 и и 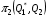 соответственно. Условия достаточности существования экстремума здесь приводим не будем. соответственно. Условия достаточности существования экстремума здесь приводим не будем.Таким образом, можно записать следующую систему: 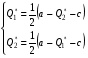  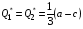 . .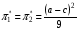 . .Итак, оптимальные стратегии фирм A и B заключаются в выборе объёмов выпуска 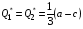 . В соответствии с определением равновесия Нэша, отклоняясь от данных уровней выпуска в единоличном порядке, фирмы могут лишь ухудшить своё положение, а именно, снизить свою прибыль. . В соответствии с определением равновесия Нэша, отклоняясь от данных уровней выпуска в единоличном порядке, фирмы могут лишь ухудшить своё положение, а именно, снизить свою прибыль.Рассмотрим графическую интерпретацию данной игры. Для этого введём понятие кривой реакции игрока. Кривую реакции игрока часто называют функцией лучших ответов. Данная кривая представляет собой геометрическое место точек, каждая из которых определяет наилучший исход для игрока при конкретном известном поведении противника. В модели Курно обозначим функции реакции игроков A и B соответственно символами 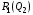 и и 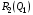 : :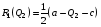 , ,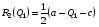 . .Здесь 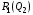 и и 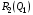 отражают оптимальные объёмы выпуска (предложения) фирм. отражают оптимальные объёмы выпуска (предложения) фирм. |
