Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.Ситуация 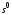 в бескоалиционной игре в бескоалиционной игре 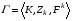 называется оптимальной по Парето, если не существует ситуации называется оптимальной по Парето, если не существует ситуации 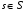 , для которой имеет место неравенство , для которой имеет место неравенство 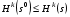 , , 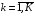 . .Другими словами, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш кого-либо из них, не уменьшив при этом выигрыш кого-либо другого. Подчеркнём формальное различие ситуации равновесия по Нэшу от ситуации, оптимальной по Парето: в первой ни один игрок, действуя в одиночку не может увеличить своего собственного выигрыша; во второй – все игроки, действуя совместно, не могут увеличить выигрыш любого игрока, не ухудшив положения другого или других игроков. В равновесии по Нэшу соглашение о выборе фиксированной ситуации равновесия удерживает каждого игрока от отклонения от неё. В оптимальной по Парето ситуации отклонившийся игрок может в некоторых случаях получить существенно больший выигрыш. В то же время сильно равновесная ситуация 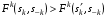 , , 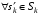 или или 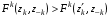 , , 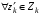 (строгие знаки неравенства) является и оптимальной по Парето. (строгие знаки неравенства) является и оптимальной по Парето.52. Позиционная форма игры.Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации. Процесс самой игры состоит в последовательном переходе от одного состояния игры к другому, который осуществляется либо путём выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом. Право выбора первого хода в позиционных играх часто определяется случайным образом. Состояния игры принято называть позициями (отсюда и название – позиционные игры), а возможные выборы в каждой позиции – альтернативами. Характерной особенностью позиционной игры является возможность представления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры П A B B B A A 1 1 1 2 2 2 2 2 2 2 1 1 1 1 Символы П, A и B в кружке указывает, кто из игроков, П, A и B, делает очередной ход. При этом символом П обычно обозначается ход в игре, осуществляемый не игроком, а каким-нибудь случайным механизмом. Например, в позиционной игре, представленной тут своим деревом, первый ход производится случайно. Пользуясь графическим описанием игры, можно сказать, что процесс игры состоит в переходе от начальной позиции к окончательной через непосредственно следующие одна за другой промежуточные позиции. Каждая окончательная вершина определяет единственную цепь (последовательность идущих друг за другом звеньев), связывающую начальную вершину сданной П A B B B A A 1 1 1 2 2 2 2 2 2 2 1 1 1 1 Такая цепь называется партией. Число различных партий равно числу окончательных вершин (позиций). В каждой окончательной позиции задан числовой выигрыш игроков. Различают позиционные игры с полной информацией и позиционные игры с неполной информацией. Позиционная игра называется игрой с полной информацией, если в любой точке любой ее партии игрок, делающий ход, точно знает, какие выборы были сделаны раньше. В игре с неполной информацией позиция дерева игры, в которой находится игрок, точно неизвестна. Этот игрок знает лишь некоторое множество позиций, в которых он потенциально может находиться на данном этапе реализации игры. Такое множество позиций называют информационным множеством игры. |
