Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb.
|
Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.Смешанная стратегия игрока – стратегия игрока, состоящая в случайном выборе им одной из своих чистых стратегий с определенной вероятностью, поэтому смешанную стратегию, например, игрока А, имеющего m чистых стратегий можно представить m-мерным вектором Р=(р1,…,рm), рi  , i=1,2,…m.Смешанной стратегией игрока называется совокупность его чистых стратегий с определёнными для них вероятностями выбора: 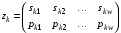 ,  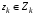,  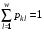.Цена игры в смешанных стратегиях – общее значение нижней и верхней цены игры в смеш.стратегиях: V=  относительно которых доказано, что они всегда существуют и равны.Нижняя цена: 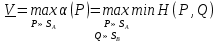  Верхняя цена игры: 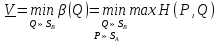  Функция 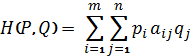 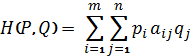определенная на декартовом произведении  множеств смешанных стратегий  и  соответственно игроков A и B и ставящая в соответствие каждой ситуации  в смешанных стратегиях  игрока A и Q =  игрока B средневзвешенный выигрыш игрока А в этой ситуации, определяемый выражением в правой части равенства , называется выигрыш-функцией игрока А в смешанных стратегиях.Выигрыш функция в смешанных стратегиях, заданную в координатной форме, можно представить и в матричной форме:  , где - вектор-строка смешанной стратегии игрока А размера [1 m]; А-матрица выигрышей игрока А в чистых стратегиях размера [mn], - вектор столбец размера [n1] смешанной стратегии игрока B. |