Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр

• Название: Задачи теории игр в экономике, финансах и бизнесе. Теория игр
• Анкор: Теория игр - теоретический материал, все вопросы.docx
• Дата: 02.05.2017
• Размер: 4.21 Mb.
• Имя файла: Теория игр - теоретический материал, все вопросы.docx
• Тип: Документы; #6343
• Категория: Математика
• страница: 8 из 27

Рисунок 5.1 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока А)

Ординаты точек, принадлежащих ломаной B₁MB^'₂ определяют минимальный выигрыш игрока A при использовании им любых смешанных стратегий. Эта минимальная величина является наибольшей в точке М, следовательно, этой точке соответствует оптимальная стратегия U^* = (, ), а ее ордината равна цене игры v.

Координаты точки M найдем, как координаты точки пересечения прямых B₁B^'₁ и B₂B^'₂.

Для этого необходимо знать уравнения прямых. Составить такие уравнения можно, используя формулу для уравнения прямой, проходящей через две точки:

Составим уравнения прямых для нашей задачи.

Прямая B₁B^'₁:

=    или   y = 4x + 2.

Прямая B₂B^'₂:

=    или   y = -x + 5.

Получим систему:

y = 4x + 2, y = -x + 5.

Решим ее:

4x + 2 = -x + 5, 5x = 3, x = 3/5, y = -3/5 + 5 = 22/5.

Таким образом, U^* = (2/5, 3/5), v = 22/5.
Аналогично решается задача по нахождению оптимальной стратегии игрока B. Разница состоит в том, что находится точка, сводящая к минимуму средний проигрыш, поэтому на рисунке 5.2 рассматривается ломаная A₂MA^'₁.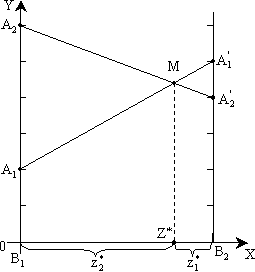
Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)

Найдем координаты точки М.

Прямая A₁A^'₁:

=  ,  откуда  y = 3x + 2.

Прямая A₂A^'₂:

=  ,  откуда  y = -2x + 6,

3x + 2 = -2x + 6, 5x = 4, x = 4/5.

Таким образом,  = 1/5,  = 4/5.
2)В общем случае схема решения игры2xnилиnx2графическим методом состоит в следующем.

1. Строят прямые, соответствующие стратегиям второго (первого) игрока.

2. Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой. Эти стратегии являются активными в оптимальной смешанной стратегии второго (первого) игрока.

3. Находят координаты точки пересечения, тем самым определяя оптимальную стратегию первого (второго) игрока и цену игры.

4. Оптимальную стратегию другого игрока находят, решая систему уравнений, включающую его активные стратегии.
Пример 5.4. Найдите решение игры, заданной матрицей:

A =

7    9   8 10   6   9

.

Решение.

Сначала проверим наличие седловой точки:  = 7,  = 9. Поскольку нижняя и верхняя цены игры не совпадают, седловая точка отсутствует, и решение следует искать в смешанных стратегиях.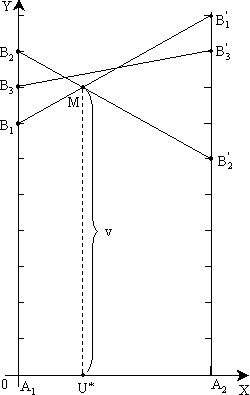

Выполним построения на плоскости XY в соответствии с методикой, приведенной выше. Результат представлен на рисунке 5.3.