Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр

• Название: Задачи теории игр в экономике, финансах и бизнесе. Теория игр
• Анкор: Теория игр - теоретический материал, все вопросы.docx
• Дата: 02.05.2017
• Размер: 4.21 Mb.
• Имя файла: Теория игр - теоретический материал, все вопросы.docx
• Тип: Документы; #6343
• Категория: Математика
• страница: 7 из 27

Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока B.

1. 
   Берем горизонтальный отрезок [0,1].
   
2. 
   В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый и правый
   
3. 
   На левом перпендикуляре вертикальной числовой оси от точки 0 его пересечения с отрезком [0,1] откладываем все элементы матрицы А, за исключением а₂₂
   
4. 
   На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все эл-ты матрицы А, за исключением а₁₁
   
5. 
   Каждый элемент на левом перпендикуляре соединим отрезком с каждым элементом на правом перпендикуляре, отличающимся от него только одним индексом. В результате получим отрезки a₁₁a₂₁ , a₁₂a₂₂, a₁₁a₁₂ и a₂₁a₂₂
   
6. 
   Находим нижнюю огибающую отрезов a₁₁a₂₁ и a₁₂a_22.
   
7. 
   Находим аивысшую точку N нижней огибающей.
   
8. 
   Находим абсциссу р⁰ наивысшей точки нижней огибающей.
   
9. 
   Смешанная стратегия Р⁰=(1-р⁰, р⁰) является оптимальной стратегией игрока А.
   
10. 
    Находим верхнюю огибающую отрезков a₁₁a₁₂ и a₂₁a₂₂.
    
11. 
    Находим наинизшую точку М верхней огибающей.
    
12. 
    Находим абсциссу q⁰ наинизшей точки верхней огибающей.
    
13. 
    Смешанная стратегия Q⁰=(1-q⁰,q⁰) является оптимальной стратегией игрока В.
    

14. Ордината наивысшей точки нижней огибающей равна ординате наинизшей точки верхней огибающей и представляет собой цену игры V.

15. Т.о. найдено геометрическими средствами решение игры {P⁰,Q⁰,V}

16. Верхний из концов нижней огибающей (лежащей на перпендикулярах) есть нижняя цена игры в чистых стратегиях

17. Нижний из концов верхней огибающей (лежащий на перпендикулярах) есть верхняя цена игры в чистых стратегиях

11. Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока A.

11. Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока B.

(!!! Помним про обозначения вероятностей чистых стратегий через p,q)

Решение игр размера 2xn или nx2 допускает наглядную геометрическую интерпретацию. Такие игры можно решать графически.

1)Дадим геометрическую интерпретацию игры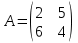


На плоскости XY по оси абсцисс отложим единичный отрезок A₁A₂ (рисунок 5.1). Каждой точке отрезка поставим в соответствие некоторую смешанную стратегию U = (u₁, u₂). Причем расстояние от некоторой промежуточной точки U до правого конца этого отрезка – это вероятность u₁ выбора стратегии A₁, расстояние до левого конца - вероятность u₂ выбора стратегии A₂. Точка А₁ соответствует чистой стратегии А₁, точка А₂ – чистой стратегии А₂.

В точках А₁ и А₂ восстановим перпендикуляры и будем откладывать на них выигрыши игроков. На первом перпендикуляре (совпадающем с осью OY) покажем выигрыш игрока А при использовании стратегии А₁, на втором – при использовании стратегии A₂. Если игрок А применяет стратегию A₁, то его выигрыш при стратегии B₁ игрока B равен 2, а при стратегии B₂ он равен 5. Числам 2 и 5 на оси OY соответствуют точки B₁ и B₂. Аналогично на втором перпендикуляре найдем точки B^'₁ и B^'₂ (выигрыши 6 и 4).

Соединяя между собой точки B₁ и B^'₁, B₂ и B^'₂, получим две прямые, расстояние от которых до оси OX определяет средний выигрыш при любом сочетании соответствующих стратегий.

Например, расстояние от любой точки отрезка B₁B^'₁ до оси OX определяет средний выигрыш игрока A при любом сочетании стратегий A₁ и A₂ (с вероятностями u₁ и u₂) и стратегии B₁ игрока B.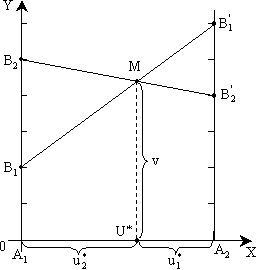