Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
|
В этой игре две равновесных по Нэшу ситуации (0, 2) и (2, 1) в чистых стратегиях. Но первая из этих ситуаций представляет собой предсказание, не являющееся разумным. Для того, чтобы исключить ситуации типа 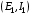 мы рассмотрим принцип последовательной рационализации: стратегия игры должна преписывать оптимальный ход в каждой вершине дерева. Т.е., если игрок находится в некоторой вершине дерева, его стратегия должна предписывать оптимальный выбор, начиная с этой точки, при данных стратегиях его оппонентов. Согласно данному принципу стратегия мы рассмотрим принцип последовательной рационализации: стратегия игры должна преписывать оптимальный ход в каждой вершине дерева. Т.е., если игрок находится в некоторой вершине дерева, его стратегия должна предписывать оптимальный выбор, начиная с этой точки, при данных стратегиях его оппонентов. Согласно данному принципу стратегия 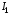 не является оптимальной, поскольку равновесной по Нэшу ситуации соответствует стратегия не является оптимальной, поскольку равновесной по Нэшу ситуации соответствует стратегия 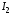 . Если игрок E вошёл на рынок, оптимальным поведением игрока I будет предоставить возможность E действовать на рынке. . Если игрок E вошёл на рынок, оптимальным поведением игрока I будет предоставить возможность E действовать на рынке.Итак, после того как E выбрал стратегию 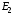 , оптимальной стратегией для игрока I будет , оптимальной стратегией для игрока I будет 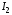 . Теперь мы можем определить оптимальное поведение фирмы E до её входа на рынок. Это можно сделать, рассмотрев редуцированную позиционную форму, где после входа на рынок игрока E принятие решения игроком I заменено на соответствующие выигрыши, которые возникают при оптимальном его поведении (рис. 8.9). . Теперь мы можем определить оптимальное поведение фирмы E до её входа на рынок. Это можно сделать, рассмотрев редуцированную позиционную форму, где после входа на рынок игрока E принятие решения игроком I заменено на соответствующие выигрыши, которые возникают при оптимальном его поведении (рис. 8.9).E не входить входить (0, 2) (2, 1) Рис. 8.9. В результате получаем простейшую задачу индивидуального решения, причём очевидным является решение игрока E войти на рынок. 56. Обратная индукция и позиционные игры с совершенной информацией. Для того, чтобы внимательнее посмотреть на обратную индукцию в конечной игре с совершенной информацией, начнём с определения оптимального «действия» в последних вершинах дерева, где принимается решение (т.е. тех вершин, для которых «последователи» – это только терминальные вершины). Решение, принимаемое игроком в такой вершине, не зависит уже от стратегического взаимодействия и потому является простой задачей принятия решения. Затем мы может обратиться к «предпоследней» вершине и найти оптимальное решение там, предвидя, естественно, ход, который будет сделан в последней вершине. И так далее. Рассмотрим следующий пример позиционной игры 1 3 2 3 3 L L R R R L (2, 0, 1) (−1, 5, 6) R L R L (3, 1, 2) (5, 4, 4) (0, −1, 7) (−2, 2, 0) Принимая оптимальные решения для третьего игрока в последних вершинах дерева, приходим к первой редуцированной игре следующего вида 1 2 L R R L (−1, 5, 6) (5, 4, 4) (0, −1, 7) Принимая оптимальное решение для второго игрока, получаем вторую редуцированную игру ( 1 L R (−1, 5, 6) (5, 4, 4) Игровая ситуация 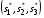 является равновесной по Нэшу. Игрок отклонившись в единоличном порядке от своей оптимальной стратегии может лишь ухудшить своё положение. Найденное решение игры проведено в соответствии с принципом последовательной рациональности. является равновесной по Нэшу. Игрок отклонившись в единоличном порядке от своей оптимальной стратегии может лишь ухудшить своё положение. Найденное решение игры проведено в соответствии с принципом последовательной рациональности.57. Модель дуополии по Штакельбергу. Дуополия по Штакельбергу – это модификация дуополии по Курно. Теперь мы считает, что есть лидер, который делает ход первым. Затем, зная этот выбор, другой игрок делает свой ход. Итак, игра протекает следующим образом:
Для нахождения равновесия воспользуемся обратной индукцией. Определим сначала функцию реагирования фирмы 2, решая задачу 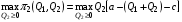 . .Привлекая необходимое условие существования экстремума получаем функцию реагирования 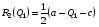 . То же самое было и в случае дуополии Курно. Разница, однако, в том, что действительная, а не гипотетическая функция реагирования фирмы 2. . То же самое было и в случае дуополии Курно. Разница, однако, в том, что действительная, а не гипотетическая функция реагирования фирмы 2.Фирма 1, естественно, также может вычислить эту функцию реагирования, а, следовательно, задача фирмы 1 выглядит так: 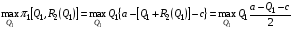 , ,что даёт 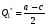 и и 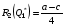 . .Прибыль в случае дуополии по Штакельбергу: 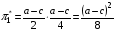 , , 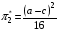 . .Для сравнения в модели Курно: 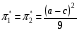 . .58. Модель последовательного торга. Рассмотрим следующую игру. Игроки 1 и 2 торгуются о разделе 1 доллара: 1-й игрок предлагает некоторый способ деления, 2-й либо принимает это предложение, либо нет; если нет, то он предлагает способ деления, а 1-й принимает, либо нет и т.д. Каждое предложение занимает один период, но при этом есть дисконтирующий множитель. Итак, формально рассмотрим следующую трёх-периодную игру. 1.а) В начале первого периода игрок 1 предлагает «свою долю» 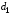 доллара, оставляя доллара, оставляя 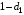 игроку 2. игроку 2.1.b) Игрок 2 принимает предложение, тогда игра заканчивается, либо отклоняет его. В этом случае игра переходит ко 2-му периоду. 2.a) В начале второго периода игрок 2 предлагает долю 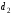 , которую получает игрок 1, оставляя себе , которую получает игрок 1, оставляя себе 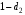 . .2.b) Игрок 1 либо принимает предложение, либо нет. В последнем случае игра переходит к 3-му периоду. 3) Игроки в третьем периоде получают доли 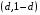 , , 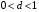 , причём d задан экзогенно. , причём d задан экзогенно.Решим данную задачу с помощью обратной индукции. Сначала вычислим, что происходит, если дело доходит до 2-го периода. Игрок 1 может получить d, если отклонит 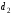 . С учётом дисконтирования (мы сравниваем стоимость в разных (соседних) периодах) игрок 1 примет . С учётом дисконтирования (мы сравниваем стоимость в разных (соседних) периодах) игрок 1 примет 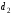 тогда и только тогда, когда тогда и только тогда, когда 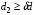 , , 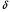 – коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением – коэффициент дисконтирования. Это значит, что задача игрока 2 состоит в выборе между получением 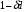 и получением и получением 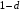 в следующем периоде. Дисконтированная стоимость последнего действия есть в следующем периоде. Дисконтированная стоимость последнего действия есть 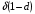 , что меньше, чем , что меньше, чем 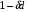 , а потому игрок 2 во втором периоде предлагает , а потому игрок 2 во втором периоде предлагает 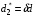 . .Таким образом, если игра доходит до второго периода, то 2-й игрок предложит 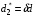 , и игрок 1 примет это предложение. , и игрок 1 примет это предложение.Однако игрок 1 может предвидеть, что игрок 2 может получить 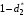 во втором периоде, отклоняя предложение во втором периоде, отклоняя предложение 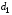 . В первом периоде стоимость . В первом периоде стоимость 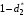 с учётом дисконтирования составит с учётом дисконтирования составит 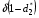 . Значит, игрок 2 принимает . Значит, игрок 2 принимает 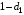 тогда и только тогда, когда тогда и только тогда, когда 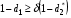 , или , или 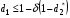 . .Поэтому задача игрока 1 в первом периоде состоит в выборе между получением 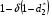 в этом периоде и получением в этом периоде и получением 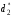 в следующем периоде. Дисконтированная величина в следующем периоде. Дисконтированная величина 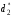 составляет составляет 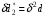 , что меньше, чем , что меньше, чем 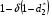 . Значит, оптимальное предложение в первом периоде есть . Значит, оптимальное предложение в первом периоде есть 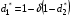 . Следовательно, в первом периоде игрок 1 предлагает . Следовательно, в первом периоде игрок 1 предлагает 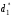 , а игрок 2 принимает это предложение и получает , а игрок 2 принимает это предложение и получает 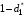 . Таким образом, выигрыш игроков есть . Таким образом, выигрыш игроков есть 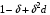 и и 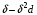 соответственно. соответственно.59. Модель «инвесторы и банк». Представим следующую ситуацию. Два инвестора вкладывают по D долларов в банк. Банк инвестировал эти средства в долгосрочный проект. Если форс-мажорные обстоятельства заставляют банк ликвидировать свои инвестиции до того, как проект «созревает», то он покрывает некоторую сумму 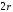 , где , где 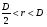 . Если банк позволяет проекту «созреть», то проект принесёт . Если банк позволяет проекту «созреть», то проект принесёт 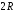 , , 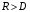 . .Есть два периода, когда вкладчики могут забрать свой вклад: период 1 – до «созревания», период 2 – после созревания. Для упрощения не будем учитывать дисконтирование. Если оба вкладчика забирают вклады в период 1, то оба получают по r и игра заканчивается. Если только один вкладчик забирает в период 1, то он получает D, а второй получает 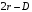 . Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает . Наконец, если ни один вкладчик не забирает в период 1, то проект «созревает», и оба вкладчика забирают свои деньги в период 2, и каждый получает по R. Если только один вкладчик забирает деньги в период 2, то он получает 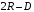 , другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому. , другой получает D. Если, наконец, ни один не забирает в период 2, то банк возвращает по R каждому.Дерево игры изображено на рис. 8.16. 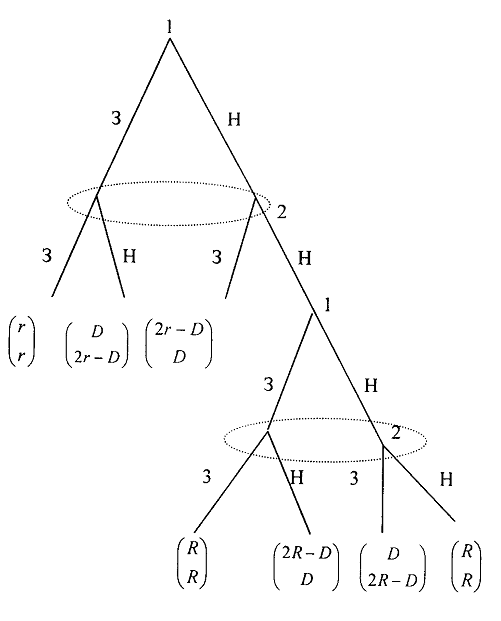 Рис. 8.16. Без строгой формализации игру в период 1 можно изобразить следующим образом:
Для периода 2:
Рассмотрим внимательно матрицу для периода 2. Поскольку 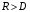 и и 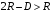 , то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1: , то в соответствии с принципом последовательной рациональности можем перейти к матрице для периода 1:
Т.к. 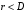 и и 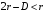 , то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R). , то получаем два равновесия по Нэшу, дающие выигрыши (r, r) и (R, R). Принцип рационализации даёт нам окончательное решение (R, R). |

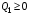 ;
;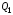 , и после этого она выбирает
, и после этого она выбирает 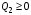 ;
;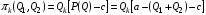 ,
, 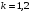 .
.