Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
49. Модель дуополии по Бертрану.Рассмотрим теперь ситуацию, когда две фирмы A и B производят однородный продукт. Предположим, что A и B одновременно и независимо объявляют цены, соответственно 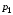 и и 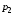 , по которым они готовы продавать свою продукцию. Тогда величина спроса на рынке для фирм A и B будет формироваться по следующему правилам соответственно: , по которым они готовы продавать свою продукцию. Тогда величина спроса на рынке для фирм A и B будет формироваться по следующему правилам соответственно: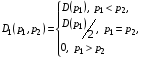 и и 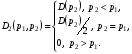 Рассмотрим условия, при которых пара 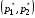 образует равновесие по Нэшу. Предположим равенство предельных затрат c фирм на выпуск продукции. Очевидно, что образует равновесие по Нэшу. Предположим равенство предельных затрат c фирм на выпуск продукции. Очевидно, что 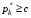 , , 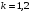 , т.к. назначение цены ниже предельных затрат приведёт к отрицательной прибыли фирм. , т.к. назначение цены ниже предельных затрат приведёт к отрицательной прибыли фирм.С другой стороны, 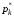 не может быть выше c. Рассмотрим это утверждение более подробно. Предположим для определённости, что не может быть выше c. Рассмотрим это утверждение более подробно. Предположим для определённости, что 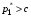 , тогда если , тогда если 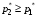 , то фирма B, сталкивающаяся в этом варианте в лучшем случае с половинным спросом, может «перехватить» весь спрос, назначив цену , то фирма B, сталкивающаяся в этом варианте в лучшем случае с половинным спросом, может «перехватить» весь спрос, назначив цену 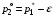 , , 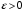 . Если же . Если же 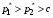 , то фирма A, аналогично, может назначить цену , то фирма A, аналогично, может назначить цену 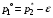 , «перехватывая» весь спрос. , «перехватывая» весь спрос.Таким образом, в равновесии по Бертрану (или в равновесии по Нэшу в дуополии по Бертрану) 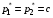 , и фирмы получают нулевую прибыль. Эту ситуацию называют парадоксом Бертрана. , и фирмы получают нулевую прибыль. Эту ситуацию называют парадоксом Бертрана.Случай дифференцируемых продуктов. Фирмы A и B выбирают цены 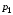 и и 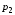 одновременно и независимо. Предположим, что спрос, с которым сталкиваются фирмы, описывается для фирм A и B соответственно функциями: одновременно и независимо. Предположим, что спрос, с которым сталкиваются фирмы, описывается для фирм A и B соответственно функциями: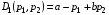 , , 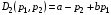 . .Стратегии фирм обозначим символами: 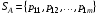 , , 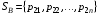 . .Прибыли (выигрыши) фирм (игроков) могут быть определены в соответствии с функциями: 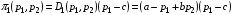 , ,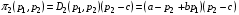 . .Если равновесная по Нэшу пара 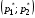 существует, то для её поиска фирмы решают следующие задачи: существует, то для её поиска фирмы решают следующие задачи: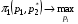 , , 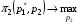 . .Решение задач запишем в виде: 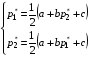  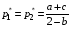 . .Итак, оптимальные стратегии фирм A и B заключаются в выборе цен 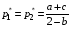 . В соответствии с определением равновесия Нэша, отклоняясь от данных уровней цен в единоличном порядке, фирмы могут лишь ухудшить своё положение, а именно, снизить свою прибыль. . В соответствии с определением равновесия Нэша, отклоняясь от данных уровней цен в единоличном порядке, фирмы могут лишь ухудшить своё положение, а именно, снизить свою прибыль.50. Модель «Проблема общего».Рассмотрим теоретико-игровую проблему, связанную с использованием некоторого общего ресурса. Данная проблема поставлена в следующей её интерпретации. Пусть в игре участвуют K фермеров. Летом их козы пасутся на зелёном поле. Обозначим через 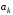 – число коз у k-го фермера. Тогда численность всего стада будет составлять величину – число коз у k-го фермера. Тогда численность всего стада будет составлять величину 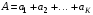 . Затраты на покупку и содержание козы равны величине c. Будем предполагать, что данная величина не зависит от количества коз в наличии у фермера. Стоимость одной козы определим как функцию . Затраты на покупку и содержание козы равны величине c. Будем предполагать, что данная величина не зависит от количества коз в наличии у фермера. Стоимость одной козы определим как функцию 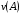 . .Предполагая, что козе необходим определённый уровень пропитания для выживания, будем считать, что существует некоторое максимальное число коз, которое может прокормиться,  . Тогда функция стоимости козы может быть описана следующим образом: . Тогда функция стоимости козы может быть описана следующим образом: , если , если  , но , но  , если , если 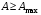 . .Весной одновременно и независимо фермеры выбирают, сколько заводить коз, т.е. определяют величину 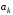 . Выигрыш . Выигрыш 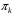 k-го фермера определим с помощью функции k-го фермера определим с помощью функции 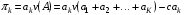 . .Таким образом, если существует равновесная по Нэшу игровая ситуация 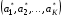 , то величина , то величина 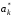 должна максимизировать функцию должна максимизировать функцию 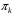 в условиях существования оптимальной ситуации для других игроков в условиях существования оптимальной ситуации для других игроков 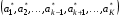 . .Решив задачи оптимизации 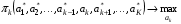 , , 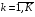 для всех участвующих в игре фермеров, получим систему: для всех участвующих в игре фермеров, получим систему: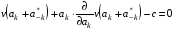 , , 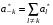 , , 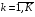 . .Решив эту систему, получим набор 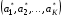 оптимальных по Нэшу стратегий игроков. оптимальных по Нэшу стратегий игроков. |
