Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Теория игр – раздел современной математики, изучающий математические модели принятия решений в т.н. конфликтных ситуациях. Математическая модель – это математическое описание компонентов и функций, отображающих существенные свойства моделируемого объекта. Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения. Игроки – заинтересованные в конфликте стороны. Стратегия – любое возможное действие игрока. Игровая ситуация – результат выбора каждым из игроков своей стратегии. Выигрыш – то, что обуславливает интерес игроков. (похвала, порицание, приз, штраф). Три вида игр:
Страховщик и страхователь На рынке есть страховщик и страхователь. Эта игра антагонистическая, так как выигрыш одного игрока равен проигрышу другого. Взаимодействие этих сторон можно рассматривать, как игру, потому что есть конфликт интересов. У каждого игрока есть свои стратегии. И они нацелены на максимизацию своего выигрыша, либо минимизацию проигрыша.
Предположим, что инвестор может купить акции одной из 3 компаний. Роль природы исполняет ситуация на фондовом рынке, которая в разные периоды складывается по-разному. Инвестору надлежит принять решение в условиях неопределенности, какой компании отдать предпочтение. На основе этих составляются матрицы выигрышей.
На рынке есть две фирмы А и В, производят аналогичные товары. Они выбирают объем производимых товаров Q1 и Q2. Если Q=0, то P=A При этом издержки у них одинаковы = C Цена зависит от Q: P(Q)=A-Q Чем больше Q, тем меньше P. Pk=(A-Q-C)*Qk Задача этой модели, найти равновесные Q1* и Q2*, которые создают ситуацию, которая является равновесием Нэша. Необходимо найти: P1(Q1;Q2*) -> max P2(Q1*;Q2) -> max
Стратегия – любое возможное действие игрока. Множество стратегий – все возможные стратегии игроков Игровая ситуация – результат выбора каждым из игроков своей стратегии. 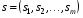 Множество игровых ситуаций – все возможные варианты игровых ситуаций. Образует ситуационное пространство игры. 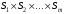 Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения. Игроки – заинтересованные в конфликте стороны. Платежная матрица – матрица, элементами корой являются выигрыши (проигрыши) игрока. Антагонистическая игра – игра с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого. FA=-FB , где F – функция выигрыша. Платежная матрица:
Матрица игровых ситуаций:
Функция выигрыша: 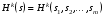 , k – игроки, s – ситуации. , k – игроки, s – ситуации.Матрица выигрышей:
Чистая стратегия игрока – стратегия, которую выберет игрок с вероятностью = 1. Доминирование - ситуация, при которой одна из стратегий некоторого игрока дает больший выигрыш, нежели другая, при любых действиях его оппонентов. Цель принципа доминирования – уменьшить размер матрицы, путем выбрасывания из рассмотрения тех стратегий, которые являются очевидно невыгодными.  4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий. 4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.Показатель эффективности: минимальный выигрыш игрока А. 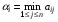 Показатель неэффективности: максимальный проигрыш игрока В. 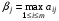 Максиминный принцип: принцип выбора эффективной стратегии, при котором максимизируется показатель эффективности. 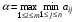 При этом выигрыш 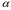 – максимин, или нижняя цена игры. – максимин, или нижняя цена игры.Минимаксный принцип: принцип выбора эффективной стратегии, при котором минимизируется показатель неэффективности. 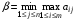 При этом проигрыш 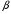 - минимакс, или верхняя цена игры.5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними. - минимакс, или верхняя цена игры.5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.Максиминный принцип: принцип выбора эффективной стратегии, при котором максимизируется показатель эффективности. 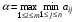 При этом выигрыш 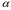 – максимин, или нижняя цена игры. – максимин, или нижняя цена игры.Минимаксный принцип: принцип выбора эффективной стратегии, при котором минимизируется показатель неэффективности. 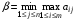 При этом проигрыш 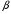 - минимакс, или верхняя цена игры. - минимакс, или верхняя цена игры.Соотношение для α и β Для элементов матрицы A имеют место неравенства 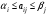 , , 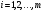 , , 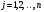 , ,и, следовательно, нижняя цена игры не больше её верхней цены в чистых стратегиях: 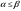 . .
Критерий решения игры в чистых стратегиях упирается в критерий существования цены игры в чистых стратегиях. Свойство: ни одному из игроков А и В, придерживающихся одной из своих оптимальных стратегий невыгодно от нее отклоняться, поскольку в этом случае он не увеличивает свой выигрыш. Цена игры в чистых стратегиях представляет собой значение выигрыша игрока А, которое он не может увеличить, если игрок В придерживается своей оптимальной стратегии и значение проигрыша игрока В, которое последний не может уменьшить при условии, что игрок А действует по своей оптимальной стратегии. Теорема: для того, чтобы существовала цена игры в чистых стратегиях, т.е. для того чтобы нижняя цена игры равнялась верхней цене игры , необходимо и достаточно существование у матрицы этой игры седловой точки. В игре без седловых точек ни у одного из игроков оптимальных стратегий нет. Т.е. задача в чистых стратегияхи меет решение, если сущ. седловая точка.
Теорема. Для элементов матрицы имеют неравенства 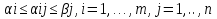 и след-ноб нижняя цена игры не больше ее верхней цены в чистых стратегиях: и след-ноб нижняя цена игры не больше ее верхней цены в чистых стратегиях: 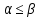 Д-во. По определению 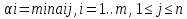 показателей эффективности показателей эффективности 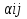 стратегий Ai и определению стратегий Ai и определению 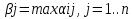 показателей неэффективности показателей неэффективности 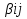 стратегий Bj игрока В имеем стратегий Bj игрока В имеем 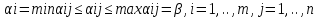 , cлед-но , cлед-но 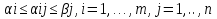 доказано доказанотак как доказанное неравенство 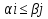 справедливо для любых i=1,..,m, j=1,..n, то оно будет справедливым в частности для номеров i=i0 и j=j0 соответственно максиминной и минимаксной стратегией Ai0 и Bj0: справедливо для любых i=1,..,m, j=1,..n, то оно будет справедливым в частности для номеров i=i0 и j=j0 соответственно максиминной и минимаксной стратегией Ai0 и Bj0: 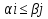 Тогда в силу 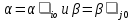 получим требуемое неравенство получим требуемое неравенство 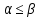
Т. Ситуация (Ai0, Bjo) будет удовлетворительна для игрока А Тогда и только тогда, когда его выигрыш 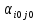 совпадет с показателем неэффективности совпадет с показателем неэффективности 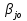 стратегии Bjo игрока В: стратегии Bjo игрока В: 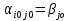 , то есть будет максимальной в j-ом столбце матрицы игры , то есть будет максимальной в j-ом столбце матрицы игрыД-во: Пусть ситауция (Ai0, Bjo) удовлетворительна для игрока А. Тогда по определению справедливо нер-во 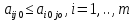 .Из этого неравенства и по определению .Из этого неравенства и по определению 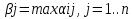 (1) показателя неэффективности стратегии Bj0 следует, что (1) показателя неэффективности стратегии Bj0 следует, что 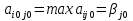 , то есть нер-во , то есть нер-во 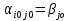 доказано. Тогда применяя (1) при j=j0 получим доказано. Тогда применяя (1) при j=j0 получим 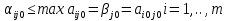 , то есть доказано , то есть доказано 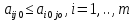
Т. Ситуация (Ai0, Bjo) будет удовлетворительна для игрока В Тогда и только тогда, когда его проигрыш 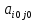 совпадет с показателем эффективности совпадет с показателем эффективности 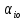 стратегии Aio игрока A: стратегии Aio игрока A: 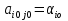 , то есть , то есть 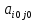 будет минимален в i-ой строке матрицы игры будет минимален в i-ой строке матрицы игрыД-во: Если ситауция (Ai0, Bjo) удовлетворительна для игрока В, то из нер-ва 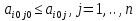 и равенства и равенства 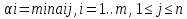 при i=i0 получим при i=i0 получим 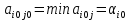 и рав-во и рав-во 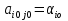 доказано доказаноЕсли же это справедливо то по 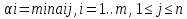 при i=i0 будем иметь при i=i0 будем иметь 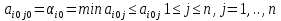 то есть доказано неравенство то есть доказано неравенство 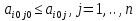
Ситуация (Ai0, Bjo) называется равновесной , если она удовлетворительна для каждого из игроков А и В то есть если выполняются неравенства 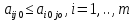 и и 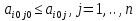 : : 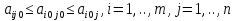 (1) или равенства (1) или равенства 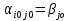 и и 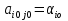 : : 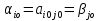 (2) (2) Таким образов двойное нер-во (1) и двойное равенство (2) эквивалентны | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

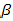
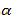
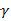
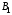
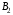
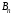
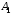
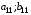
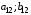
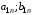
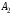
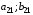
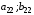
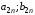
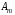
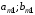
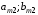
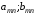
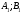
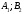
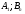
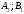
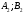
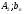
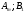
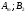
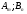
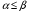 .
.