Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.Нижней ценой (или максимином)матричной игры в смешанных стратегиях называется величина 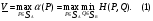 Верхней ценой (или минимаксом)матричной игры в смешанных стратегиях называется величина 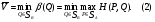 Докажем существование нижней и верхней цен в смешанных стратегиях, т.е. достижимость максимума в (1) и минимума в (2). Необходимость этого доказательства возникает по причине бесконечности множеств SAв (1) и SBв (2). Сначала докажем вспомогательные предложения. Лемма 1. Соответствие, сопоставляющее каждой смешанной стратегии Р  SAигрока А показатель ее эффективности α(Р),является числовой функцией, определенной на симплексе SA,аналитическое выражение которой задается равенством SAигрока А показатель ее эффективности α(Р),является числовой функцией, определенной на симплексе SA,аналитическое выражение которой задается равенством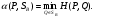 Аналогично, соответствиеβ(Q),задаваемое формулой 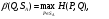 является числовой функцией, определенной на симплексеSBи ставящей в соответствие каждой смешанной стратегииQ  SBигрока В показатель ее неэффективностиβ(Q). SBигрока В показатель ее неэффективностиβ(Q). Доказательство. Для каждой смешанной стратегии P  SAв силу теоремы 1 - для каждой смешанной (в частности, чистой) стратегии Р SAв силу теоремы 1 - для каждой смешанной (в частности, чистой) стратегии Р  SAигрока А существует (достигается) SAигрока А существует (достигается) 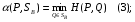 для каждой смешанной (в частности, чистой) стратегии Q  SBигрока В существует (достигается) SBигрока В существует (достигается) 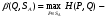 существует число существует число 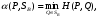 которое по определению минимума является единственным. Следовательно, α(Р)- числовая функция векторного аргумента Р, определенная на симплексе SA. которое по определению минимума является единственным. Следовательно, α(Р)- числовая функция векторного аргумента Р, определенная на симплексе SA.Аналогичной аргументацией обосновывается, что 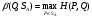 является числовой функцией векторного аргумента Q, определенного на симплексе SB. является числовой функцией векторного аргумента Q, определенного на симплексе SB. Лемма 2. Функцииα(Р) иβ(Q)непрерывны в своих областях определения SAиSB. Оставим без доказательства. Теперь докажем следующую теорему. Теорема 2. Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях. Доказательство. Так как функция α(Р)по лемме 2 непрерывна на компакте SA, то она достигает на этом множестве своего максимума, т.е. существует нижняя цена игры в смешанных стратегиях: 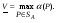 Аналогичным образом обосновывается существование и верхней цены игры в смешанных стратегиях: 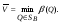 Смешанная стратегия PО  SA,максимизирующая показатель эффективности α(Р) (существование которой доказано в теореме 2), назовем максиминной смешанной стратегией игрока А. Таким образом, нижняя цена игры SA,максимизирующая показатель эффективности α(Р) (существование которой доказано в теореме 2), назовем максиминной смешанной стратегией игрока А. Таким образом, нижняя цена игры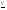 есть (см. 1) показатель эффективности максиминной смешанной стратегии PО: есть (см. 1) показатель эффективности максиминной смешанной стратегии PО: 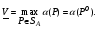 В частном случае PО =Аi0 является максиминной чистой стратегией игрока A. Аналогично, смешанная стратегия QО  SB(существование которой доказано в теореме 2), минимизирующая показатель неэффективности β(Q), назовем минимаксной смешанной стратегией игрока В.Показатель неэффективности минимаксной смешанной стратегии QОравен верхней цене игры SB(существование которой доказано в теореме 2), минимизирующая показатель неэффективности β(Q), назовем минимаксной смешанной стратегией игрока В.Показатель неэффективности минимаксной смешанной стратегии QОравен верхней цене игры 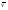 (см. 2)): (см. 2)): 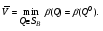 Если QО=Bj0, то Bj0является минимаксной чистой стратегией. |
