Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Аналитическое решение игры 2×2 в смешанных стратегиях.
Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке. Для игры, в которой отсутствует седловая точка оптимальное решение игры существует и определяется парой смешанных стратегий (x1*,x*2) и (у1*,у2*). (!!!это заменяем на следующее обозначение смешанных стратегий P0 =(p10;p20) andQ=(q10;q20), соответственно дальше меняем сами)
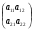 Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры. Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры.
Средний выигрыш первого игрока, если он использует оптимальную смешанную стратегию х*=(x1*,x*2), а второй игрок – чистую стратегию, соответ.первому столбцу платежной матрицы, равен цене игры v: a11 x1*+a21 x*2 = v. Тот же средний выигрыш получает первый игрок, если второй игрок применяет стратегию, соответ.второму столбцу платежной матрицы, т.е. a12 x1*+a22 x*2 = v. Учитывая, что x1*+ x*2=1, получаем систему уравнений для определения оптимальной стратегии первого игрока и цены игры: a11 x1*+a21 x*2 = v. a12 x1*+a22 x*2 = v x1*+ x*2=1 Решая эту систему, получим оптимальную стратегию x1*= x2*= и цену игры v =
В=-АТ= Применяя теорему об активных стратегиях при отыскании оптимальной смешанной стратегии второго игрока, получаем, что при любой чистой стратегии первого игрока средний проигрыш второго игрока равен v, т.е. a11 у1*+ a12 у2*=v. Тогда оптимальная стратегия второго игрока определяется по формулам: у1*= у2*= v’=-v
Итак, мы можем сформулировать общий алгоритм геометрического нахождения оптимальных стратегий игрока А, цены игры, нижней и верхней цены игры в чистых стратегиях, седловых точек матрицы и доминирующих стратегий игроков.
Мы дали геометрическую интерпретацию оптимальных стратегий игрока А. Если матрица игры содержит седловую точку, то автоматически выявляется и оптимальная стратегия игрока В. Но можно достаточно удовлетворительно проинтерпретировать геометрически оптимальную стратегию игрока В и в случае отсутствия седловых точек. |