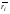Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Критерий Байеса оптимальности чистых стратегий относительно выигрышей.Пусть известны состояния П 1 … П n и вероятности q1 … qn , с которыми природа П реализует эти состояния. Тогда мы находимся в ситуации принятия решения в условиях риска. Показателем эффективности стратегии 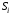 по критерию Байеса относительно выигрышей называется среднее значение, или математическое ожидание выигрыша i-й строки с учётом вероятностей всех возможных состояний природы: по критерию Байеса относительно выигрышей называется среднее значение, или математическое ожидание выигрыша i-й строки с учётом вероятностей всех возможных состояний природы: 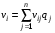 , , 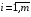 . .Оптимальной среди чистых стратегий по критерию Байеса относительно выигрышей считается стратегия 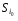 с максимальным показателем эффективности: с максимальным показателем эффективности: 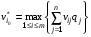 (матрица выигрышей), (матрица выигрышей), 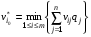 (матрица потерь). (матрица потерь).Критерий Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия Sio является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот. Пример.
Для матрицы выигрышей: 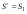 , , 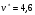 . Для матрицы потерь: . Для матрицы потерь: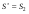 , , 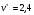
Рассмотрим игру с природой с матрицей, в которой известны вероятности состояния природы q1 .. qn. При принятии решения в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы исходной, использую формулу рисков: r i,j = 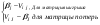 Показателем неэффективности стратегии Si по критерию Байеса относительно рисков называется среднее значение (мат ожидание) рисков i-й строки матрицы А, вероятности которых, совпадают с вероятностями природы. Пусть средний риск при стратегии Si равен 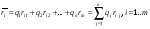 Показателем неэффективности стратегии 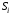 по критерию Байеса относительно рисков называется среднее значение рисков i-й строки матрицы рисков: по критерию Байеса относительно рисков называется среднее значение рисков i-й строки матрицы рисков: 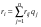 . Соответствующий критерий: . Соответствующий критерий: 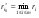 . .Тогда оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия Sio, показатель неэффективности которой минимален, т.е. минимален средний риск. 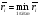 Критерий Байеса относительно выигрышей и относительно рисков эквивалентны, т.е. если стратегия Sio является оптимальной по критерию Байеса относительно выигрышей, то она является оптимальной и по критерию Байеса относительно рисков, и наоборот. Пример для матрицы выигрышей.
Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S1 является оптимальной по критерию Байеса относительно рисков, так как наименьший показатель неэффективности именно у этой стратегии (0,6). 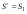 , , 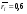
|

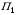 ,
, 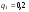
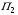 ,
, 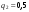
 ,
,