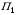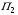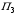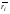Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Критерий Лапласа оптимальности чистых стратегий относительно выигрышей.Часто складывается такая ситуация, когда мы лишены возможности определить вероятности состояния природы. Критерий основан на принципе недостаточного основания. Здесь все вероятности состояний природы признаются равновероятными: 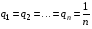 . Тогда показателем эффективности стратегии . Тогда показателем эффективности стратегии 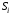 по критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышей i-й строки: по критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышей i-й строки: 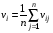 . . Оптимальной среди чистых стратегий по критерию Лапласа относительно выигрышей считается стратегия 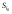 с максимальным показателем эффективности: с максимальным показателем эффективности: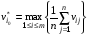 (матрица выигрышей), (матрица выигрышей), 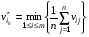 (матрица потерь). (матрица потерь).Очевидно, что критерий Лапласа относительно выигрышей есть частный случай критерия Байеса относит выигрышей при 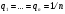 . .
Для матрицы выигрышей: 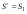 , , 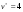 . Для матрицы потерь: . Для матрицы потерь: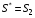 , , 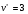
Рассмотрим игру с природой с матрицей, в которой известны вероятности состояния природы q1 .. qn. При принятии решения в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы исходной, использую формулу рисков: r i,j = 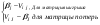 Критерий Байеса относительно рисков при равновероятных состояниях природы 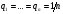 превращается в критерий Лапласа относительно рисков. Тогда величина превращается в критерий Лапласа относительно рисков. Тогда величина 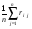 , или более простая , или более простая 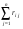 , представляет собой показатель неэффективности стратегии Si по критерию Лапласа относительно рисков. , представляет собой показатель неэффективности стратегии Si по критерию Лапласа относительно рисков.Следовательно, оптимальной среди чистых стратегий по критерию Лапласа относительно рисков является стратегия Sio, показатель неэффективности 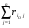 которой минимален: которой минимален: 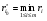 . .Пример для матрицы выигрышей.
Из наибольшего числа каждого столбца вычитаем каждое число данного столбца. Стратегия S1 является оптимальной по критерию Байеса относительно рисков, так как наименьший показатель неэффективности именно у этой стратегии (0,6). 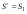 , , 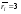
Критерий Вальда есть частный случай обобщенного критерия Гурвица относительно выигрышей со специальными коэффициентами 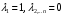 Оптимальной среди чистых стратегий по критерию Вальда считается та стратегия, при которой минимальный выигрыш является максимальным среди минимальных выигрышей всех чистых стратегий. 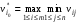 для матрицы выигрышей, для матрицы выигрышей,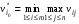 для матрицы потерь. для матрицы потерь.Критерий Вальда является критерием крайнего пессимизма, т.к. ориентирует игрока А на наихудшее для него состояние природы и, следовательно, на крайне осторожное, осмотрительное поведение при выборе стратегий. Этот критерий уместен в тех случаях, когда игрок А не столько хочет выиграть, сколько не хочет проиграть.
Является противоположностью критерия Вальда. Представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей, когда коэф. выбираются следующим образом: 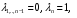 Оптимальной среди чистых стратегий по максимаксному критерию является стратегия Аio с максимальным показателем эффективности: 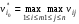 для матрицы выигрышей, для матрицы выигрышей,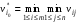 для матрицы потерь. для матрицы потерь.Т.е. стратегия, максимальный выигрыш при которой максимален среди максимальных выигрышей всех чистых стратегий. Поэтому оптимальной будет стратегия, при которой (хотя бы) один из выигрышей является максимальным среди выигрышей всех чистых стратегий .Оптимальная по максимаксному критерию стратегия гарантирует игроку А возможность наибольшего выигрыша, равного максимаксу. Для максимаксного критерия показатели пессимизма и оптимизма равны соответственно 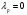 , ,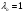 . Таким образом, максимаксный критерий является критерием крайнего оптимизма, так как ориентирует ЛПР на наилучшее, благоприятнейшее для него состояния природы и, следовательно, на порой неоправданно легкомысленное поведение при выборе стратегий. Вместе с тем, в некоторых ситуациях этим критерием пользуются осознанно, например, в ситуации когда перед игроком стоит дилемма: либо получить наибольший выигрыш, либо стать банкротом. . Таким образом, максимаксный критерий является критерием крайнего оптимизма, так как ориентирует ЛПР на наилучшее, благоприятнейшее для него состояния природы и, следовательно, на порой неоправданно легкомысленное поведение при выборе стратегий. Вместе с тем, в некоторых ситуациях этим критерием пользуются осознанно, например, в ситуации когда перед игроком стоит дилемма: либо получить наибольший выигрыш, либо стать банкротом.
Критерий Гурвица был выдвинут в 1951 году Леонидом Гурвицем, как некоторая альтернатива, попытка разработать промежуточный критерий, который учитывает критику критериев Вальда и максимакса. В научной литературе он именуется критерием Гурвица: «Критерий пессимизма-оптимизма Гурвица с коэффициентом оптимизма λ 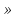 [0,1] оптимальности чистых стратегий относительно выигрышей». [0,1] оптимальности чистых стратегий относительно выигрышей».Данный критерий позволяет учитывать комбинацию наихудших состояний. Смысл его состоит в нахождении по специальной формуле эффективности всех стратегий игрока А и последующее сравнении данных показателей эффективности для выбора наиболее оптимальной стратегии, при условии полной неопределённости, т.е. вероятности состояния природы нам неизвестны. Другими словами, при выборе решения мы находим некоторый средний результат при состоянии, находящемся между крайним пессимизмом и безудержным оптимизмом. Критерий Гурвица целесообразно применять в следующих ситуациях:
Рассмотрим игру с природой размера m x n, m 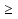 2, n 2, n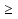 2, с матрицей A= (aij), где i=1,2,…,m, а j=1,2,…,n. Пусть A1 ,A2 ,…,Am – чистые стратегии игрока А и П1,П2,...Пn – состояния природы П. Вероятности состояний неизвестны. 2, с матрицей A= (aij), где i=1,2,…,m, а j=1,2,…,n. Пусть A1 ,A2 ,…,Am – чистые стратегии игрока А и П1,П2,...Пn – состояния природы П. Вероятности состояний неизвестны.Введём специальный коэффициент λ 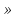 [0,1], которым обозначим количественную «меру оптимизма» игрока А при выборе стратегии. Данный коэффициент выбирает сам игрок, на основании интуиции, личного опыта, состояния окружающей среды или на основе статистических исследований результатов принятия решений. [0,1], которым обозначим количественную «меру оптимизма» игрока А при выборе стратегии. Данный коэффициент выбирает сам игрок, на основании интуиции, личного опыта, состояния окружающей среды или на основе статистических исследований результатов принятия решений.Эффективность чистой стратегии Ai в смысле критерия Гурвица [(Hur)p (λ)] характеризуется показателем: (Hur)pi (λ)= (1- λ)Wi + λMi , i = 1,2,…,m, (2.1) где Wi и Mi - показатели эффективности стратегии Ai соответственно по критерию Вальда и по максимаксному критерию. Таким образом, Игрок А при использовании критерия Гурвица с коэффициентом λ 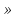 [0,1] занимает более взвешенную позицию, чем если бы он применил критерий Вальда или максимаксный критерий. [0,1] занимает более взвешенную позицию, чем если бы он применил критерий Вальда или максимаксный критерий.Если открыть скобки в равенстве (2.1) и несколько преобразовать данное выражение, то можно получить показатель эффективности (Hur)pi (λ) в форме линейной функции от аргумента λ 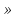 [0,1] с угловым коэффициентом (Mi -Wi): [0,1] с угловым коэффициентом (Mi -Wi):(Hur)pi (λ) = (Mi -Wi) λ + Wi (2.2) Ценой игры в чистых стратегиях по критерию Гурвица с коэффициентом оптимизма λ относительно выигрышей или (Hur)p (λ)-ценой в чистых стратегиях называется максимальный из показателей эффективности: 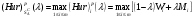 (2.3) (2.3)Оптимальной во множестве чистых стратегий по критерию Гурвица с коэффициентом λ относительно выигрышей, или (Hur)p (λ) – оптимальной во множестве 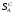 , называется чистая стратегия Ak с наибольшим (Hur)p (λ)-показателем эффективности: , называется чистая стратегия Ak с наибольшим (Hur)p (λ)-показателем эффективности: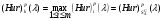 (2.4) (2.4)Из определений (2.2) и (2.3) очевидно, что критерий Гурвица оптимальности чистых стратегий относительно выигрышей при λ = 0 превращается в критерий Вальда оптимальности чистых стратегий, а при λ = 1 – в максимаксный критерий оптимальности чистых стратегий. Составим общий алгоритм нахождения оптимальной чистой стратегии игрока А относительно выигрышей с использованием критерия Гурвица: 1) Выбираем по строкам наименьший выигрыш и заполняем колонку Wi ; 2)Выбираем по строкам наибольший выигрыш и заполняем колонку Mi ; 3)Находим эффективность чистой стратегии по формуле: (Hur)pi (λ)= (1- λ)Wi + λMi ; результаты заносим в соответствующую колонку в таблицу; 4)По методу максимина (критерий Вальда) и максимакса определяем наибольший из всех расчётных выигрышей в колонках Wi и Мi; по наибольшему значению (Hur)pi определяется оптимальная чистая стратегия данного игрока. 5)Для разрешения конфликтной ситуации составляем таблицу Гурвица относительно игрока В. В таблице меняем платёжную матрицу. 6)Далее также применяем обобщенный критерий Гурвица и метод максимина относительно игрока В. 7)Игрок, разрешающий конфликтную ситуацию определяется по наибольшему расчётному выигрышу из соответствующих оптимальных стратегий игроков, т.е. используется формула 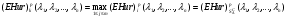 . .Выбор показателя оптимизма λ логичен: вместо того, чтобы придерживаться двух крайностей в оценке ситуации в большинстве случаев целесообразно придерживаться некоторой промежуточной позиции, которая учитывает как наихудшее, так и наилучшее поведение природы.
Коэффициент оптимизма λ выбирается между 0 и 1, при этом если коэффициент равен 1, то критерий Гурвица превращается в критерий Вальда (по пессимизму результата), если коэффициент равен 0, то в критерий Севиджа. Число (1- λ) будет характеризовать меру пессимизма игрока А, поэтому в данной работе будем называть коэффициентом пессимизма. Таким образом коэффициенты оптимизма и пессимизма в сумме дают единицу. С увеличением меры ответственности коэффициент λ стремится к нулю: чем серьезнее последствия ошибочных решений, тем больше желание ЛПР перестраховаться. А чем ближе λ к нулю, тем ближе (1- λ) к единице, т.е. тем больше пессимизма. И наоборот. Заметим, что при коэффициенте λ=0,5 видно нейтральность игрока в оценивании ситуации при выборе стратегии. λ1, λ2,…, λn – числовые коэффициенты количественно характеризующие субъективную оценку игрока А в играх с природой. Такое положение делает обобщенный критерий Гурвица в большей степени субъективным, чем объективным. На результат выбора данной стратегии могут влиять различные ситуации, при которых известны возможные выигрыши. Существуют некоторые методы выбора данных коэффициентов. Так Лабскер предлагает математико-формализованный метод, для ограничения степени полного произвола субъективного выбора игрока А, который будет разобран ниже. В.Б. Волгоградский предлагает иной подход к выбору коэффициентов, который состоит в том, что игрок А сначала субъективно определяет числовое значение показателя своего оптимизма λо 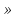 [0,1], а затем в зависимости от этого значения определяет коэффициенты λj, j=1,2,…,n, по следующей формуле: [0,1], а затем в зависимости от этого значения определяет коэффициенты λj, j=1,2,…,n, по следующей формуле: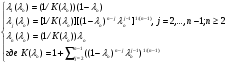 (5.1) (5.1)Матиматико-формализованный подход Лабскера выбора коэффициентов λ зависит от средних выигрышей и носит менее субъективный характер, чем модель, предложенная Волгоградским. Её суть заключается в следующем: Рассматривается игра с природой размером mxn, в которой матрица А является матрицей выигрышей игрока А, матрица B – матрица ранжированных выигрышей. Считается, что все выигрыши положительные. Далее используется специальная формула в зависимости от ситуации (думаю формулу учить не надо): 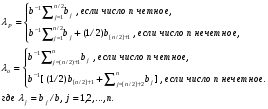 (5.2) (5.2)Где λо – показатель оптимизма, λP – показатель пессимизма; b – сумма всех выигрышей матрицы, b-1 необходимо для выведения среднего значения выигрышей j-го ранга; 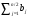 - сумма выигрышей bij j-го ранга; λ j = b j / b – выражение коэффициентов λj через выигрыши. - сумма выигрышей bij j-го ранга; λ j = b j / b – выражение коэффициентов λj через выигрыши.
Весь выигрыш Игрока зависит от того, какой коэффициент оптимизма он выберет. Он может рискнуть и попробовать выиграть большую сумму, а может не рисковать и с уверенностью выиграть меньшую сумму. Таким образом игрок может быть пессимистом, крайним оптимистом или нейтралом. Коэффициент оптимизма λ выбирается между 0 и 1, при этом если коэффициент равен 1, то критерий Гурвица превращается в критерий Вальда (по пессимизму результата), если коэффициент равен 0, то в максимаксный – то есть игрок будет крайним оптимистом.. Число (1- λ) будет характеризовать меру пессимизма игрока А, поэтому в данной работе будем называть коэффициентом пессимизма. Таким образом коэффициенты оптимизма и пессимизма в сумме дают единицу. С увеличением меры ответственности коэффициент λ стремится к нулю: чем серьезнее последствия ошибочных решений, тем больше желание ЛПР перестраховаться. А чем ближе λ к нулю, тем ближе (1- λ) к единице, т.е. тем больше пессимизма. И наоборот. Заметим, что при коэффициенте λ=0,5 видно нейтральность игрока в оценивании ситуации при выборе стратегии.
Данный критерий позволяет учитывать комбинацию наихудших состояний. Смысл его состоит в нахождении по специальной формуле эффективности всех стратегий игрока А и последующее сравнении данных показателей эффективности для выбора наиболее оптимальной стратегии, при условии полной неопределённости, т.е. вероятности состояния природы нам неизвестны. Другими словами, при выборе решения мы находим некоторый средний результат при состоянии, находящемся между крайним пессимизмом и безудержным оптимизмом. Критерий Гурвица целесообразно применять в следующих ситуациях:
Рассмотрим игру с природой размера m x n, m 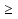 2, n 2, n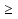 2, с матрицей A= (aij), где i=1,2,…,m, а j=1,2,…,n. Пусть A1 ,A2 ,…,Am – чистые стратегии игрока А и П1,П2,...Пn – состояния природы П. Вероятности состояний неизвестны. 2, с матрицей A= (aij), где i=1,2,…,m, а j=1,2,…,n. Пусть A1 ,A2 ,…,Am – чистые стратегии игрока А и П1,П2,...Пn – состояния природы П. Вероятности состояний неизвестны.Введём специальный коэффициент λ 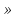 [0,1], которым обозначим количественную «меру оптимизма» игрока А при выборе стратегии. Данный коэффициент выбирает сам игрок, на основании интуиции, личного опыта, состояния окружающей среды или на основе статистических исследований результатов принятия решений. [0,1], которым обозначим количественную «меру оптимизма» игрока А при выборе стратегии. Данный коэффициент выбирает сам игрок, на основании интуиции, личного опыта, состояния окружающей среды или на основе статистических исследований результатов принятия решений.Эффективность чистой стратегии Ai в смысле критерия Гурвица [(Hur)p (λ)] характеризуется показателем: (Hur)pi (λ)= (1- λ)Wi + λMi , i = 1,2,…,m, (2.1) где Wi и Mi - показатели эффективности стратегии Ai соответственно по критерию Вальда и по максимаксному критерию. Таким образом, Игрок А при использовании критерия Гурвица с коэффициентом λ  [0,1] занимает более взвешенную позицию, чем если бы он применил критерий Вальда или максимаксный критерий. [0,1] занимает более взвешенную позицию, чем если бы он применил критерий Вальда или максимаксный критерий.Если открыть скобки в равенстве (2.1) и несколько преобразовать данное выражение, то можно получить показатель эффективности (Hur)pi (λ) в форме линейной функции от аргумента λ  [0,1] с угловым коэффициентом (Mi -Wi): [0,1] с угловым коэффициентом (Mi -Wi):(Hur)pi (λ) = (Mi -Wi) λ + Wi (2.2) Ценой игры в чистых стратегиях по критерию Гурвица с коэффициентом оптимизма λ относительно выигрышей или (Hur)p (λ)-ценой в чистых стратегиях называется максимальный из показателей эффективности: 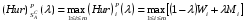 (2.3) (2.3)Оптимальной во множестве чистых стратегий по критерию Гурвица с коэффициентом λ относительно выигрышей, или (Hur)p (λ) – оптимальной во множестве 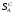 , называется чистая стратегия Ak с наибольшим (Hur)p (λ)-показателем эффективности: , называется чистая стратегия Ak с наибольшим (Hur)p (λ)-показателем эффективности: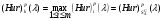 (2.4) (2.4)Природа может находиться в самом выгодном положении с вероятностью λ и в самом невыгодном с вероятностью (1- λ). Можно также трактовать параметр λ как степень оптимизма лица, принимающего решения. |