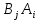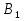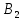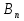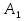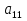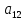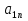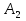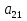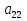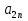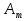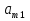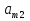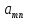Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр

• Название: Задачи теории игр в экономике, финансах и бизнесе. Теория игр
• Анкор: Теория игр - теоретический материал, все вопросы.docx
• Дата: 02.05.2017
• Размер: 4.21 Mb.
• Имя файла: Теория игр - теоретический материал, все вопросы.docx
• Тип: Документы; #6343
• Категория: Математика
• страница: 12 из 27

Решение матричной игры m×n сведением к задаче линейного программирования для игрока A.

Пусть дана матричная игра с матрицей А порядка m х n.

			…
			…
			…
…	…	…	…	…
			…

А=

P^o=(p1^o,p2^o,…,pm^o)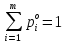

,

Если игрок А применяет любую смешанную стратегию P=(p1,p2,…,pm) против любой чистой стратегии B_j игрока В, то он получает выигрыш

F(P,B_j)=a₁jp₁+a₂jp₂+…+a_njp_m, j=1,2,…,n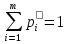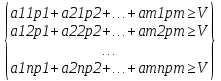

.



Разделим каждое неравенство на V>0 и введем

x1=p1/v, x2=p2/v,…,xm=pm/v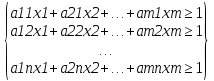



Разделив на V>0 равенство 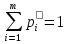, получим выражение x1+x2+…+xm=1/v

Получаем задачу линейного программирования для игрока А:

x1+x2+…+xm->min(поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры vбыла максимальной)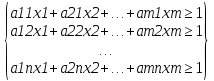



P^o=(p1^o=x₁^o*V, p₂^o=x₂^o*V,…,p_m^o=x_m^o*V)

11. Решение матричной игры m×n сведением к задаче линейного программирования для игрока B.

Пусть дана матричная игра с матрицей А порядка m х n.

			…
			…
			…
…	…	…	…	…
			…

А=

Q^o=(q1^o,q2^o,…,qn^o)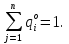



Если игрок В применяет любую смешанную стратегию Q=(q1,q2,…,qm) против любой чистой стратегии A_i игрока A, то он получает проигрыш

F(P,B_j)=a₁jq₁+a₂jq₂+…+a_njq_m, j=1,2,…,n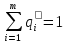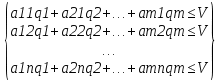

.



Разделим каждое неравенство на V>0 и введем

y1=q1/v, y2=q2/v,…,ym=qm/v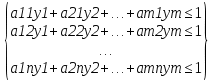



Разделив на V>0 равенство 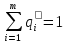, получим выражение y1+y2+…+ym=1/v

Получаем задачу линейного программирования для игрока В:

y1+y2+…+ym->max (поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры vбыла наименьшей)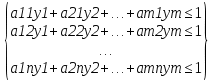



Q^o=(q1^o=y₁^o*V, q₂^o=y₂^o*V,…,q_m^o=y_m^o*V)