Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.Некооперативная или бескоалиционная игра, это система Г= (aij,bij)=(Ha(Ai,Bj), Hb(Ai,Bj)), где Ai и Bj принадлежат Sa и Sb соответственно, а Ha и Hb функции выигрыша. Sa и Sb – множество стратегий игрока А и В Sa= {A1,A2, … , Am}, Sb = {B1,B2, … , Bn}. Бескоалиционное поведение, когда соглашения между участниками запрещены правилами, а кооперативное поведение разрешается в форме выбора совместных стратегий. Интересы игроков могут пересекаться, быть взаимовыгодными обоим игрокам, в то время как в антагонистическом конфликте это не представляется возможным. Матрица выигрышей двух игроков в бескоалиционной игре имеет следующий вид S= Sa x Sb:
Неантагонистические игры, как и антагонистические, могут быть как конечные, так и бесконечные. Эта характеристика игры зависит от количества чистых стратегий игроков (S1, S2, … ,Sk где k- количество игроков, конечны) Способы задания игр:
В теории игр, игра в нормальной форме (или стратегической форме) состоит из трех элементов: множества игроков, множества чистых стратегий каждого игрока, множества платежных функций каждого игрока. Таким образом, игру в нормальной форме можно представить в виде матрицы, которая имеет следующий вид S= Sa x Sb:
Чистая стратегия даёт полную определённость каким образом игрок продолжит игру. В частности, она определяет результат для каждого возможного выбора, который игроку может придётся сделать. Пространством стратегий называют множество всех чистых стратегий доступных данному игроку. Действие игрока, состоящее в случайном выборе одной из своих стратегии с определенной вероятностью, называется смешанной стратегией. Если Si – конечное множество чистых стратегий игрока i, то смешанная стратегия ∂i : Si → [0,1] ставит в соответствие каждой чистой стратегии Si вероятность ∂i(Si) >= 0 того, что она будет играться, причем сумма всех вероятностей равна 1. Смешанная стратегию игрока "А"
где A1, A2 - стратегии игрока "A", а p1, p2 - соответственно вероятности (частоты), с которыми эти стратегии применяются, причем p1 + p2 = 1. Аналогично смешанная стратегию игрока "В"
где B1, B2 - стратегии игрока "B", а q1, q2 - соответственно вероятности, с которыми эти стратегии применяются, причем q1 + q2 = 1. Существуют ситуации доминирования стратегий, т.е. ситуации, когда один из игроков никогда не будет применять одну стратегию в пользу другой, потому что та будет приносить ему больший выигрыш. Итак, стратегии могут доминировать как строго, так и слабо. Чистая стратегия 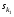 k-го игрока строго доминируема (строго доминируется), если существует другая чистая стратегия k-го игрока строго доминируема (строго доминируется), если существует другая чистая стратегия 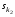 такая, что такая, что 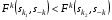 для для 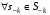 . .Чистая стратегия 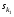 k-го игрока слабо доминируема (слабо доминируется), если существует другая чистая стратегия k-го игрока слабо доминируема (слабо доминируется), если существует другая чистая стратегия 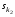 такая, что такая, что 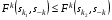 для для 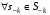 . .Смешанная стратегия 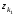 k-го игрока строго доминируема (строго доминируется), если существует другая чистая стратегия k-го игрока строго доминируема (строго доминируется), если существует другая чистая стратегия 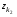 такая, что такая, что 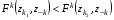 для для 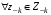 . .Смешанная стратегия 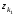 k-го игрока слабо доминируема (слабо доминируется), если существует другая чистая стратегия k-го игрока слабо доминируема (слабо доминируется), если существует другая чистая стратегия 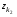 такая, что такая, что 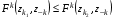 для для 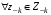 . . |
