Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.В играх с природой игроку приходится не только выбирать стратегии для достижения оптимального выигрыша, но и учитывать риски принимаемых решений. Таким образом, критерий Гурвица можно определить относительно рисков, в данном случае, критерий будет представлять собой комбинацию критерия Сэвиджа и миниминного критерия. Этот критерий будем называть критерием пессимизма-оптимизма Гурвица относительно рисков, или (Hur)r (λ)-критерием, где λ В качестве показателя неэффективности чистой стратегии Ai по критерию Гурвица относительно рисков [ (Hur)r (λ) ] рассматривается число: 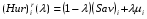 , i=1,2,…,m (1.1) , i=1,2,…,m (1.1)где (Sav)i и µi – показатели неэффективности стратегии Ai соответственно по критерию Сэвиджа и по миниминному критерию. Показатели неэффективности чистой стратегии можно записать в следующей форме: 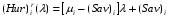 , λ , λ Из которой понятно, что 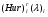 является линейной функцией аргумента λ является линейной функцией аргумента λ 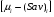 . . Ценой игры в чистых стратегиях ( 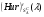 ) по критерию Гурвица относительно рисков является наименьший из показателей неэффективности всех чистых стратегий: ) по критерию Гурвица относительно рисков является наименьший из показателей неэффективности всех чистых стратегий: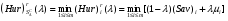 , λ , λ Чистую стратегию Ak с наименьшим показателем неэффективности называется оптимальной во множестве чистых стратегий по критерию Гурвица относительно рисков, т.е.: 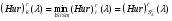 , λ , λ Использую формулу (1.1), находим 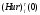 =(Sav)i и =(Sav)i и 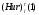 = = 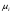 . Таким образом видно, что критерий Гурвица оптимальности чистых стратегий относительно рисков при λ = 0 превращается в Критерий Сэвиджа оптимальности чистых стратегий, а при λ = 1 – в миниминный критерий оптимальности чистых стратегий. . Таким образом видно, что критерий Гурвица оптимальности чистых стратегий относительно рисков при λ = 0 превращается в Критерий Сэвиджа оптимальности чистых стратегий, а при λ = 1 – в миниминный критерий оптимальности чистых стратегий.
При использовании этого критерия исходная платёжная матрица заменяется матрицей Гермейера. Каждый элемент матрицы мы домножаем на соответствующую вероятность j состояния природы. 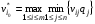 для матрицы выигрышей, для матрицы выигрышей,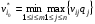 для матрицы потерь. для матрицы потерь.Критерий Гермейера применяют игроки не склонные к риску, т.к. каждая стратегия оценивается с точки зрения min по гарантиров. результата. Состояние природы образует минимум а затем игрок выбирает стратегию которая принесёт ему максимальный результат. Т.е. он защищает себя. Пример. Исходная матрица
Далее умножаем каждый элемент в столбце на соответствующий коэффициент q. Получим следующую таблицу :
В столбце VGi в. Находим миним. Элементы по строкам , а в столбце VGi п. находим макс. Элементы. Далее находим VGi в (maxmin) , и VGi п. (minmax) Получаем следующий ответ : S*=S3 , V*=0,6 - выигрыш S*=S2 , V*=2,8 - потеря |
