Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
53. Понятие о конечных играх с совершенной информацией.Любая игра 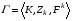 называется конечной, если она содержит конечное число игроков (k) функции выигрышей k-го игрока ( называется конечной, если она содержит конечное число игроков (k) функции выигрышей k-го игрока (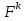 ). В игре с совершенной информацией все действия игроков идут последовательно, а не одновременно. Игроки наблюдают действия природы. ). В игре с совершенной информацией все действия игроков идут последовательно, а не одновременно. Игроки наблюдают действия природы.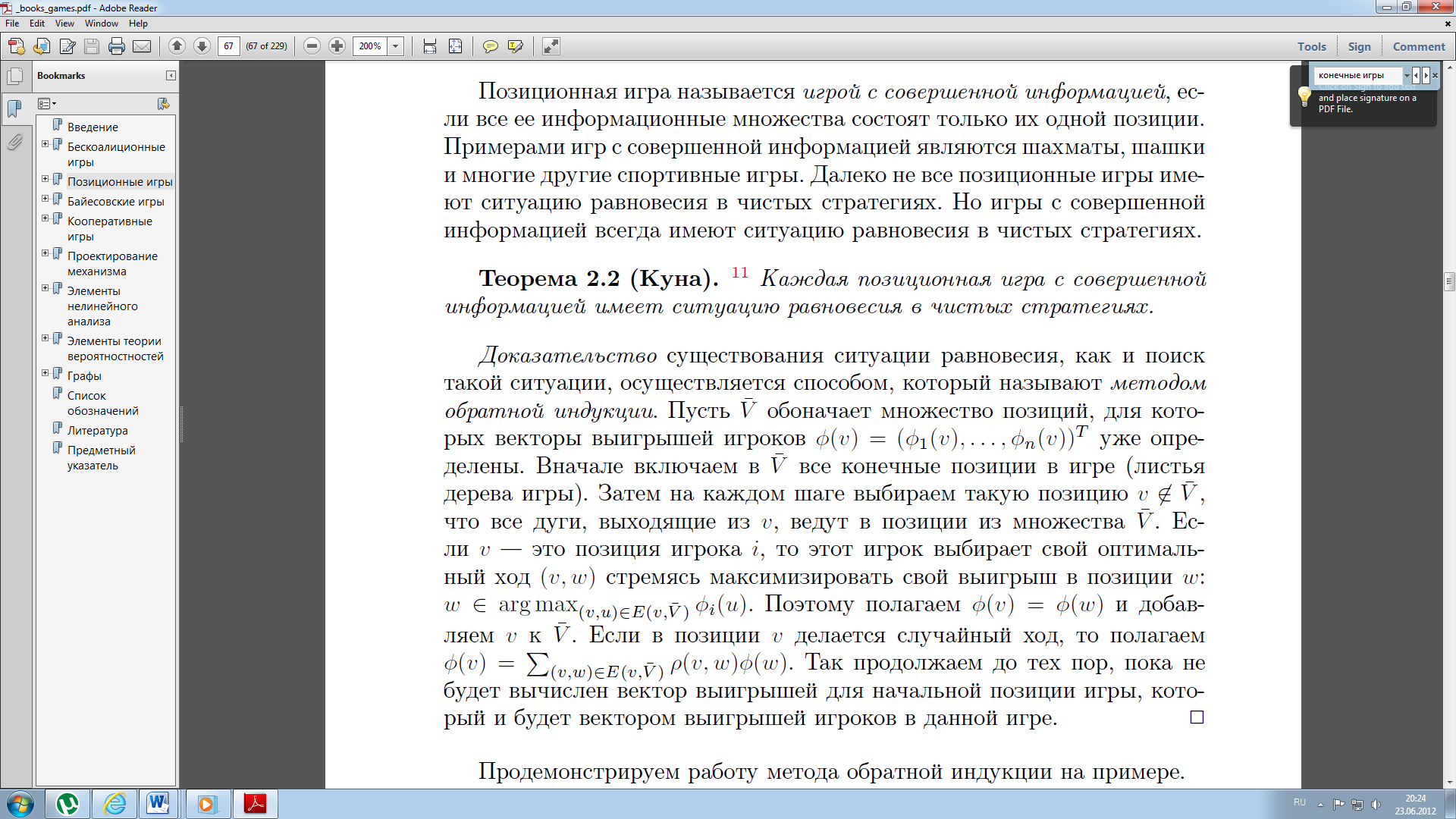  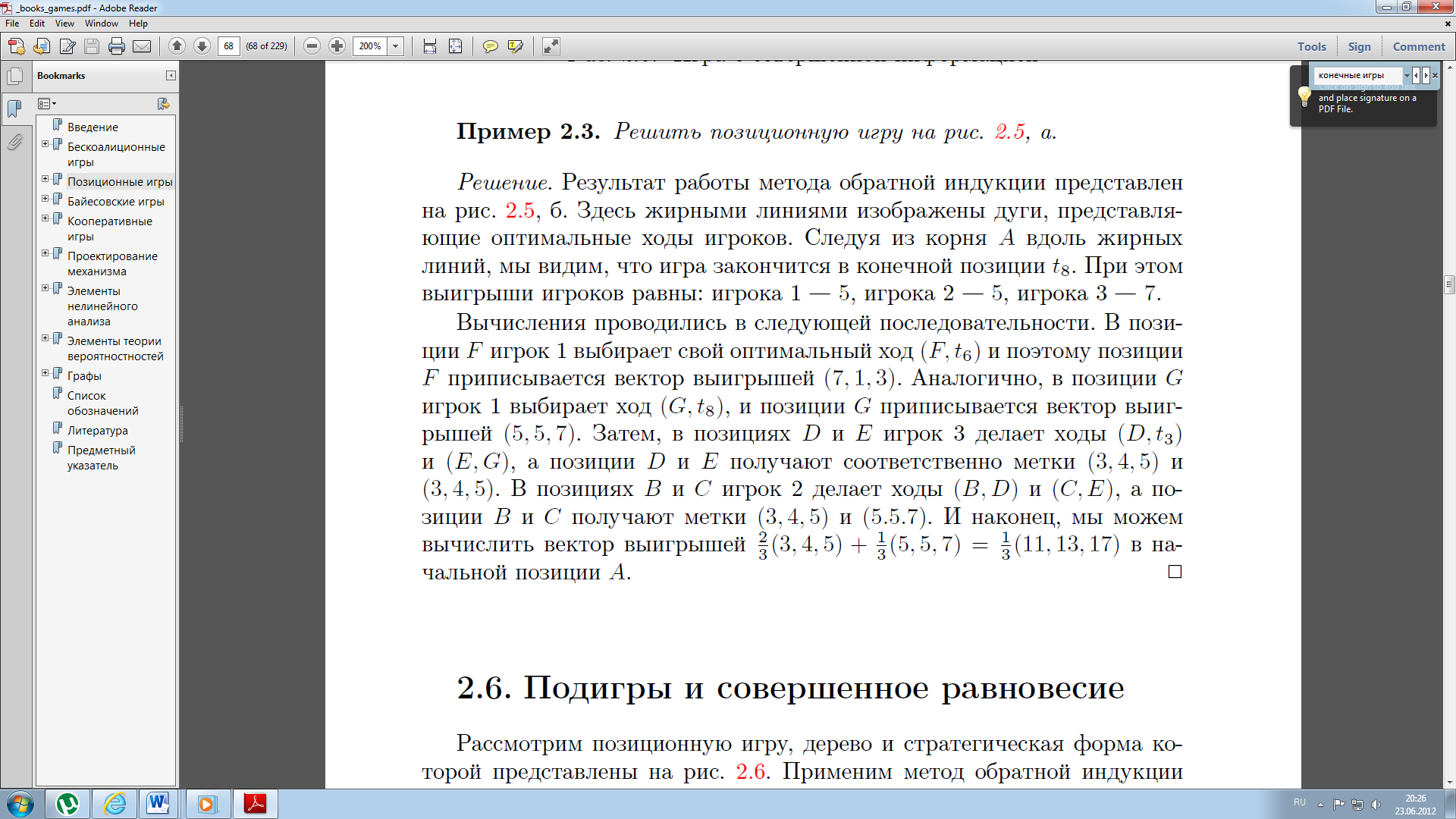 54. Стратегическая форма позиционной игры с совершенной информацией. Отметим очень важное обстоятельство. Имея набор стратегий каждого игрока, мы можем построить нормальную, или стратегическую, форму данной игры. Заранее определённую последовательность ходов игрока, выбранную им в зависимости от информации о ходах другого игрока и ходах природы, будем называть чистой стратегией этого игрока. В том случае, если в игре нет случайных ходов, выбор игроком A и игроком B чистых стратегий однозначно определяет исход игры – приводит к окончательной позиции, где игрок A и получает свой выигрыш. Именно это обстоятельство позволяет сводить позиционную игру к матричной игре. Процесс сведения позиционной игры к матричной называется нормализацией позиционной игры. Пример. Рассмотрим в позиционной форме обобщённую неантагонистическую игру двух игроков A и B с совершенной информацией. У игрока A две чистые стратегии: 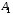 – выбрать U, – выбрать U, 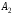 – выбрать D. – выбрать D.У игрока B четыре стратегии: 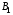 – – 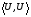 , выбрать U при любом выборе игрока A; , выбрать U при любом выборе игрока A;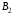 – – 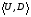 , выбрать U, если игрок A выбрал U и выбрать D, если игрок A выбрал D; , выбрать U, если игрок A выбрал U и выбрать D, если игрок A выбрал D;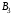 – – 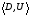 , выбрать D, если игрок A выбрал U и выбрать U, если игрок A выбрал D; , выбрать D, если игрок A выбрал U и выбрать U, если игрок A выбрал D;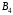 – – 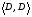 , выбрать D при любом выборе игрока A. , выбрать D при любом выборе игрока A.Дерево игры представлено на рис. 8.7. A B B  U U D D D U 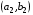 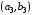 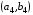 Рис. 8.7 Здесь пары 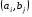 отражают выигрыши игроков в каждом из четырёх исходов игры. Нормализация игры даёт следующую таблицу выигрышей игроков: отражают выигрыши игроков в каждом из четырёх исходов игры. Нормализация игры даёт следующую таблицу выигрышей игроков:
55. Равновесие по Нэшу в позиционной игре с совершенной информацией. Теорема. В конечной игре с совершенной информацией существует равновесие по Нэшу в чистых стратегиях. Пример 6. Фирма E (entrant) – новичок – рассматривает вопрос о том, входить ли на рынок, где в текущий момент есть одна единственная укоренившаяся фирма I (incumbent). Если E решается на вход, то I может ответить двумя способами: она может предоставить вход, отдавая часть своих продаж, но, не изменяя цену, либо она может вступить в хищническую войну, которая приведёт к «драматическому» снижению цен. Дерево данной игры представлено на рис. 8.8. E I не входить входить (0, 2) война предоставить (−3, −1) (2, 1) Рис. 8.8. Стратегии игрока E: 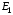 – не входить на рынок – не входить на рынок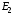 – входить на рынок. – входить на рынок.Стратегии игрока I: 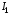 – объявить войну игроку E, если он вошёл в рынок; – объявить войну игроку E, если он вошёл в рынок;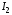 – предоставить игроку E вход, отдавая часть своих продаж, но, не изменяя цену. – предоставить игроку E вход, отдавая часть своих продаж, но, не изменяя цену. Соответствующая игре нормальная форма имеет вид:
| |||||||||||||||||||||||||||||||||||