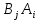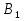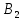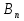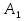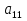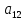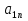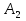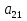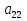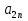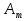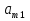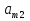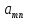Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Доминирование смешанных стратегий для игрока B.Один из способов упрощения игр основывается на принципе доминирования, который позволяет в некоторых случаях игру с матрицей А свести к эквивалентной игре с матрицей меньшего размера.
А= Между смешанными (в том числе и чистыми) стратегиями 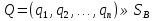 игрока В и выпуклыми комбинациями игрока В и выпуклыми комбинациями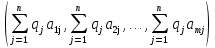 T, T, 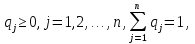 столбцов 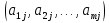 T , j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы T , j=1,2,…,n, матрицы А (Т- значок транспонирования), представляющими собой столбцы 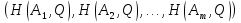 T Tпроигрышей Н( 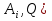 , i=1,2,…,m, игрока В в ситуациях ( , i=1,2,…,m, игрока В в ситуациях (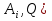 , i=1,2,…,m, устанавливается взаимно-однозначное соответствие , i=1,2,…,m, устанавливается взаимно-однозначное соответствие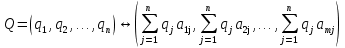 T , T ,из которого видно, что, в частности, каждой чистой стратегии 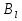 , l=1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l-й столбец , l=1,2,…,n, игрока В ставится во взаимно-однозначное соответствие l-й столбец 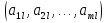 T матрицы А. T матрицы А.Если для двух выпуклых комбинаций столбцов матрицы А 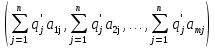 T T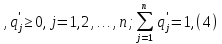 и 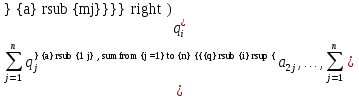 T T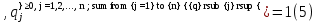 выполняются неравенства 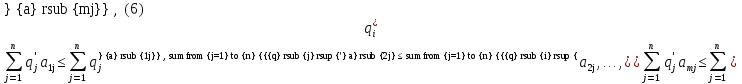 то говорят, что столбец (4) (стратегия 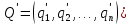 доминирует столбец (5) (стратегию доминирует столбец (5) (стратегию 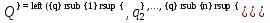 , а столбец (5) (стратегия , а столбец (5) (стратегия 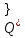 ) доминируется столбцом (4) (стратегией ) доминируется столбцом (4) (стратегией 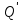 ). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии ). Если каждое неравенство (6) является равенством, то столбцы (4) и (5) (стратегии 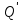 и и 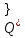 ) называют дублирующими друг друга. Если же каждое неравенство (6) является строгим, то говорят, что столбец (4) (стратегия ) называют дублирующими друг друга. Если же каждое неравенство (6) является строгим, то говорят, что столбец (4) (стратегия 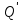 ) строго доминирует столбец (5) (стратегию ) строго доминирует столбец (5) (стратегию 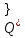 ), а столбец (5) (стратегия ), а столбец (5) (стратегия 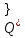 ) строго доминируется столбцом (4) (стратегией ) строго доминируется столбцом (4) (стратегией 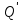 ). ). Таким образом, по данным определениям для игрока В предпочтительными оказываются доминирующие стратегии. |