Теория игр - теоретический материал, все вопросы. Задачи теории игр в экономике, финансах и бизнесе. Теория игр
 Скачать 4.21 Mb. Скачать 4.21 Mb.
|
Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.12. Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре. Для каждой смешанной стратегии 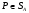 игрока игрока 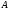 существует существует 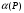 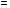 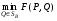 ;(4.1) ;(4.1)Для каждой смешанной стратегии 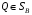 игрока игрока 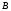 существует существует 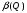 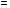 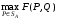 . (4.2) . (4.2)Доказательство: Для проведения доказательства введём понятие симплекса Стандартным n-симплексом называется подмножество пространства 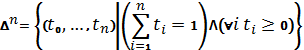 Его вершинами являются точки: … Сначала покажем, что симплекс является ограниченным замкнутым множеством, т.е. компактом. Рассмотрим симплекс в евклидовом пространстве 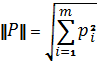 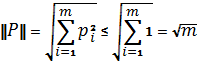 Пусть последовательность точек сходится к точке Так как Таким образом, предельная точка Аналогично и симплекс Если зафиксировать произвольную смешанную стратегию 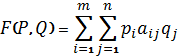 видно, что она непрерывна по аргументу Q на множестве Аналогично доказывается и существование (4.2). Теорема доказана. |
