Курс содержит четыре раздела элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов
 Скачать 2 Mb.
|
|
ВВЕДЕНИЕ Курс содержит четыре раздела: элементы теории множеств, алгебра логики, элементы комбинаторики и теория графов. Целью данного курса является дать слушателям основные понятия дискретной математики, которые необходимы для дальнейшего обучения данной специальности. Основные понятия теории множеств составляют базовый язык математики (а значит, и дискретной) и поэтому необходимы для изучения остальных разделов. Работа компьютеров основана на двоичной системе счисления и поэтому все преобразования информации осуществляются по законам алгебры логики. Известны также применения алгебры логики при анализе алгоритмов программ, синтезе управляющих систем. Основные понятия комбинаторики необходимы для изучения курса теории вероятностей. В экономических исследованиях также нередко возникают задачи, которые решаются с использованием методов комбинаторики. Теория графов применяется для решения задач в различных областях науки и техники, в том числе и в экономике, например, для решения задач нахождения кратчайших маршрутов в транспортных сетях. Для изучения данного курса студентам достаточно знаний математики в объеме средней школы. I. ТЕОРИЯ МНОЖЕСТВ 1. Основные понятия теории множеств. 1.1. Множества и подмножества В математике понятия множества и его элементов, так же как понятия точки, прямой, вектора, относятся к исходным понятиям и никак не определяются. Мы будем понимать под множеством всякую совокупность каких-либо объектов. Объекты этой совокупности есть элементы данного множества. Обычно множества обозначаются прописными, а элементы множества строчными буквами. Хотя от этого соглашения придется иногда отступать, т.к. элементами некоторого множества могут быть другие множества. Принадлежность элемента a множеству А обозначается a∈A Если элемент b не принадлежит множеству А, то, в этом случае, используется обозначение b ∉ A. П р и м е р ы. 1) А– множество жителей в г. Новосибирске. 2) C – множество планет Солнечной системы. 3) D – множество действительных чисел;  ∈D. 4) N – множество натуральных чисел; 1, 2 ∈N; ∉ N. Напомним, что для числовых множеств приняты следующие обозначения: N – множество натуральных чисел, Z – множество целых чисел, Q – множество всех рациональных чисел, R – множество вещественных чисел, C – множество комплексных чисел. Множество A называется подмножеством множества B, если всякий элемент множества A является элементом множества B, т.е.  .При этом используется обозначение ⊆. Знак ⊆ называется знаком включения. В этом случае говорят, что В содержит А или множество А содержится в множестве В или имеется включение множества А в множество В. Этот факт математически можно записать так А⊆В. Таким образом, записи А⊆В и равносильны.П р и м е р. Справедливы следующие включения: N⊆Z, Z⊆Q, Q⊆R, R⊆C. Множества А и B равны , если их элементы совпадают, т.е. если А⊆В и В⊆А. В этом случае пишут A=B. Обычно для доказательства равенства двух множеств и доказывают два включения А⊆В и В⊆А. Если элементы множеств А и не совпадают, то эти множества не равны (обозначение A≠B). Из приведенного определения равных множеств следует, что множество полностью определяется своими элементами. Если A⊆В и , A≠B то A называется строгим подмножеством B. Обозначение A⊂ B (знак ⊂ называется знаком строгого включения). Свойства множеств: 1. А  В  А В и А В.2. А В АВ или А=В.3. А В  А В.4. А В АВ.5. А В и ВС АС.6. А В и ВС АС.7. А В и ВС АС.Множества могут быть конечными (состоящие из конечного числа элементов) и бесконечными. Число элементов в конечном множестве называется мощностью и обозначается |A|. О мощности бесконечного множества будет говориться в следующих разделах. Множество мощности 0, т.е. не содержащее элементов, называется пустым и обозначается ∅. Принято считать, что пустое множество является подмножеством любого множества. Множество, содержащее все элементы всех подмножеств, принимающих участие в решении какой-либо задачи, называют основным или универсальным множеством и обозначают символом U, т.е. если в решении какой-либо задачи принимают участие множества А={a} и B={b,c}, то U ={a,b,c}. Максимально возможное число подмножеств универсального множества называют семейством подмножеств универсального множества. Это семейство включает пустое подмножество, само универсальное множество и множества, сформированные по одному, два, три и т.д., элементов универсального множества. Формирование выборок по одному, два, три и т.д. элементов реализуется процедурой комбинаторики - сочетанием. Семейство подмножеств универсального множества обозначают символом B(U) или 2U и называют булеаном множества U. Например, если U={a,b,c}, B(U)={, {a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}}. Легко видеть, что число элементов булеана B(U) зависит от числа элементов универсального множества U по формуле: |B(U)|=2|U|. Например, если |U|=3 имеем |B(U)|=23=8. Число элементов булеана B(U)-есть его мощность |B(U)|. Понятие булеана применимо не только к универсальному множеству, но и к любому другому множеству  . Тогда он обозначается, соответственно 2А.П р и м е р ы:
вообще для любого nмножество {n}⊆ 2N, множество {1,…n}⊆2N , множество {n: n=2k, k=1,2,…}⊆2N и т.п. 1.2. Способы задания множества. Рассмотрим способы задания конкретных множеств. Для конечного множества, число элементов которого относительно невелико, может быть использован способ непосредственного перечисления принадлежащих ему элементов. Элементы конечного множества перечисляют в фигурных скобках в произвольном порядке {1,3,5}. Поскольку множество полностью определено своими элементами, то при задании конечного множества порядок, в котором перечислены его элементы не имеет значения. Поэтому записи {1,3,5}, {3,1,5}, {5,3,1} и т.д. все задают одно и то же множество. Кроме того, иногда в записи множеств используют повторения элементов. Будем считать, что запись {1,3,3,5,5} задает то же самое множество, что и запись {1,3,5}. В общем случае для некоторого конечного множества А, состоящего из n элементов используют форму записи А={а1,а2,…,аn}или А={x1,x2,…xn}. Как правило, при этом избегают повторений элементов. Указанный способ задания множества путем непосредственного перечисления его элементов применим в весьма узком диапазоне конечных множеств. Наиболее общим способом задания конкретных множеств является указание некоторого свойства, которым должны обладать все элемента описываемого множества, и только они. В качестве такого свойства также может быть использована некоторая процедура, описывающая способ получения элементов множества из уже полученных элементов либо из других объектов. Такое свойство называется характеристическим свойством или характеристическим предикатом и обозначается P(x). При подстановке конкретного значения х = а выражение Р(а) принимает значение “истина” или “ложь”, т.е. Р(х) есть логическая функция. Аргументами предиката могут быть не только числа, но и объекты любой природы. Пусть имеется свойство P, которым могут обладать или не обладать элементы некоторого универсального множества U. Тогда множество А, состоящее из всех элементов множества U, обладающих свойством P, будет обозначаться одним из следующих способов: А={x:P(x)}, или А={x: x обладает свойством P}. Например, А={x: x есть четное натуральное число} Означает, что А есть множество, состоящее из всех таких элементов x, что каждое из них есть натуральное число. Или, например, свойство, определяющее множество G={x: x есть студент второго курса специальности 080109} формирует в буквальном смысле некоторый коллектив. Таким образом, характеристический предикат множества есть тот закон, посредством которого совокупность элементов объединяется в единое целое. Предикат, задающий коллективизирующее свойство может быть тождественно ложным, т.е. не выполняться ни для каких элементов универсального множества. Тогда множество, определяемое таким предикатом, не будет иметь ни одного элемента, т.е. будет пустым множеством. П р и м е р ы задания множеств: 1) Множество А ={x: x=π/2+2πk, k=0,±1,±2,…} есть множество решений уравнения sinx=1. 2) Множество чисел Фибоначи F = {fn= fn-1+ fn-2, n=2,3,…; f0=1, f1=1} В этом примере в качестве характеристического предиката используется процедура вычисления элементов множества по уже известным его элементам. 3) К = {(x,y): x2 + y2 ≤ 1}− множество точек единичного круга на плоскости; 4) L = {x: sin x < 0,5}− множество действительных чисел, синус которых меньше 0.5. 2. Алгебра множеств 2.1. Основные операции над множествами. Рассмотрим операции над множествами, которые позволяют из уже имеющихся множеств образовывать новые множества. Для любых двух множеств определим следующие основные операции.
 Здесь знак  - означает «или».Операторная запись объединения имеет вид: union(A,B)={x|xA или xB}.
 Здесь знак  - означает «и».Операторная запись пересечения имеет вид: intersection(A,B)={x|xA и xB}. 3. Дополнение множества Aэто множество всех элементов универсального множества, не принадлежащих A.  ,Операторная запись дополнения имеет вид: complement(A)= {x|xU и xA}. Операции дополнения, пересечения и объединения определяют две дополнительные операции: разности и симметрической разности.
 5. Симметрическая разность или кольцевая сумма множеств А, В - множество всех таких x, что x – элемент А, но не элемент В или x – элемент В, но не элемент А. 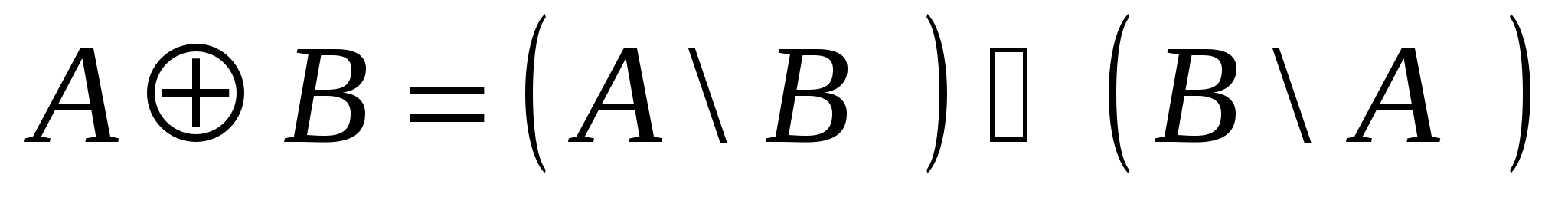 П р и м е р ы на объединение множеств:
A={x: x= π/2 +2πk, k=0,±1,±2,…}  {x: x= -π/2+2πk, k=0,±1,±2,…,}
D2 = {(x,y): x  ,  } }П р и м е р ы на пересечение множеств: 1) Пусть А={a,b,c}, B={a,d,e,f}, тогда А  В = {a}.
множество В содержит единственный элемент – точку (0,0). П р и м е р на разность двух множеств: В отличие от операций объединения и пересечения разность строго двуместна, т.е. определена только для двух множеств.
С в о й с т в а операции «разность»: 1) разность определена только для двух множеств; 2) разность некоммутативна, т.е. А\В ≠ В\А 3) если А\В = ∅, то А  В. |
Аm , где Аm = {(x,y): x2 + y2 ≤ 
} – круг радиуса 1/m, тогда