ЛОГИКА. Лекция понятие определение понятия, его структура и представление понятия в естественном языке понятие это форма мысли, в которой предмет мысли отображается в его общих и существенных признаках. Расшифруем термины, используемые в этом определении
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
Лекция 1. ПОНЯТИЕ ОПРЕДЕЛЕНИЕ ПОНЯТИЯ, ЕГО СТРУКТУРА И ПРЕДСТАВЛЕНИЕ ПОНЯТИЯ В ЕСТЕСТВЕННОМ ЯЗЫКЕ Понятие – это форма мысли, в которой предмет мысли отображается в его общих и существенных признаках. Расшифруем термины, используемые в этом определении. Форма мысли – это то же самое, что и разновидность мысли. Ещё древние греки установили, что когда человек практикует познающее мышление, он может это делать тремя способами. Самый элементарный процесс познания состоит в отличении рассматриваемого предмета от всех других предметов. Эта способность человека фиксируется в понятии. После того, как человек опознал предмет, он начинает приписывать ему некоторые свойства, и результат этой деятельности фиксируется в высказываниях или суждениях. Наконец, когда человек обладает некоторой информацией, зафиксированной в нескольких суждениях, он на основе этой информации может строить новое суждение с новой информацией, и эта способность человека отражена в умозаключениях. Таким образом, когда утверждается, что понятие – это форма мысли, тем самым указывается на первую, самую элементарную способность человека к познающему мышлению. Предмет мысли – это предмет, который попал во внимание человека. При этом рассматриваемым предметом может быть не только реально существующий предмет, например стол, но и абстрактный предмет, например синус угла, и даже в принципе не существующий предмет, например квадратный треугольник. Признак – это то, чем один предмет отличается от других предметов, или то общее, что есть у нескольких предметов. Примеры признаков: стеклянный, высотой свыше 180 см, твёрдый, лежащий на поверхности стола, который находится в комнате на втором этаже. Каждый предмет имеет практически бесконечное число признаков. Это обусловлено тем, что все признаки бывают двух типов: собственные и относительные. Собственный признак – это признак, характеризующий какое-либо качество предмета. Примерами собственного признака являются признаки деревянный, упругий, плавающий. Относительный признак – это признак, возникающий при соотнесении рассматриваемого предмета с каким-либо другим предметом. Примеры относительных признаков – стоящий справа от стула, находящийся на высоте 2 м, обладающий высотой выше 3 м. Поскольку мысленно каждый предмет можно соотнести с любым другим предметом или с несколькими другими предметами, которых практически бесконечное множество, то и признаков возникает огромное количество. Общий признак – это признак, который принадлежит нескольким, как минимум двум, предметам. Примеры общих признаков – белый, твёрдый, написанный от руки. Помимо общих признаков, существуют единичные признаки, которые принадлежат одному и только одному предмету. Пример единичного признака – самая высокая гора в мире. Ещё одним термином, через который раскрывается смысл понятия, является существенный признак. Существенный признак – это признак, без которого предмет мысли в принципе не может существовать. Это определение одновременно задаёт процедуру отделения существенных признаков от несущественных. Если предмет можно представить без рассматриваемого признака, то такой признак несущественный. Если же такое представление невозможно, то признак существенный. Примерами существенных признаков ручки (которой пишут на бумаге) являются имеющая массу, имеющая длину, помещающаяся в руке, предназначенная для того, чтобы оставлять чернильный след на бумаге, т. к. без этих признаков невозможно представить себе ручку. Несущественными признаками ручки будут имеющая зелёный корпус, шариковая, оставляющая чернильный след, т. к. можно представить себе ручку перьевую с красным корпусом, в которой закончились чернила. Таким образом, в качестве итога можно сказать, что понятие выражает способность человека узнавать предмет, т. е. отличать его от всех других предметов на основе его существенных признаков. Человек понимает, что представляет собой тот или иной предмет, если обладает понятием этого предмета. Структура понятия состоит из трёх элементов: содержания, объёма и имени. Имя – это слово или сочетание слов, выражающих понятие на естественном языке. Имена бывают двух видов: простые и составные. Простое имя состоит только из одного слова. Обычно простым именем является имя существительное. Примеры простых имён – стол, стул, ручка. Составное имя состоит из нескольких слов. Примеры составных имён – деревянный стол, стул с высокой спинкой, ручка, лежащая на поверхности деревянного стола. Объём понятия – это совокупность всех предметов, обозначаемых именем понятия. Содержание понятия – это множество всех признаков, принадлежащих всем предметам из объёма рассматриваемого понятия. Например, объём понятия «автомобиль» составляет множество всех автомобилей, а содержание понятия «автомобиль» включает такие признаки, как имеющий колёса, имеющий систему управления, являющийся транспортным средством, хотя далеко ими не ограничивается. 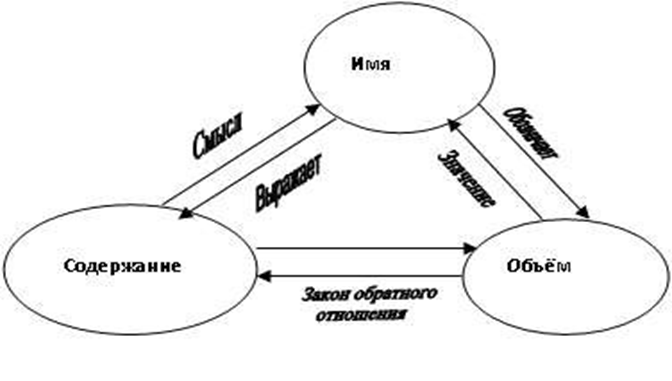  Рис. 1. Структура понятия Графически структура понятия представлена на рис. 1. Эта схема носит название семантического треугольника. На схеме показаны отношения между именем понятия, его содержанием и объёмом. Имя понятия обозначает любой предмет из объёма понятия, а объём, со своей стороны, является значением имени. С другой стороны, имя выражает содержание понятия, а содержание является смыслом имени. Между содержанием и объёмом понятия существует связь, выражаемая законом обратного отношения. Этот закон утверждает, что, чем богаче содержание понятия, т. е. чем больше признаков в его составе, тем меньше объём понятия, и наоборот, чем беднее содержание, тем больше предметов входит в объём понятия. Для примера сравним содержания и объёмы понятий «человек» и «европеец». Содержание понятия «человек» включает такие признаки, как млекопитающее, прямоходящее, обладающее разумом и т. д. Объём понятия «человек» включает всех людей, живущих на Земле. Содержание понятия «европеец» включает все признаки содержания понятия «человек» плюс один дополнительный признак – постоянно проживающий на территории Европы. Объём понятия «европеец» включает всех людей, постоянно проживающих на территории Европы. Сравнивая попарно объёмы и содержания этих понятий, можно заметить, что объём понятия «человек» больше объёма понятия «европеец», а содержание понятия «европеец» включает на один признак больше содержания понятия «человек». Следует различать понятие и представление о предмете. Представление – это образ предмета, возникающий в сознании при упоминании о предмете. Представление множественно, т. е. сколько людей, представляющих предмет, столько представлений. В отличие от представления понятие непредставимо и единично, т. е., если два человека способны узнать один и тот же предмет, то оба они обладают одним и тем же понятием. Наличие у понятия объёма и. содержания позволяет ввести в рассмотрение две оценочные характеристики понятия – точность и ясность. Ясность – это характеристика понятия, объём которого хорошо известен, т. е. про любой предмет можно однозначно сказать, входит он в объём рассматриваемого понятия или нет. Если существую предметы, которые трудно отнести или не отнести к объёму понятия, то такое понятие неясное. Пример неясного понятия – маленький человек, т. к. затруднительно сказать, является ли высокий ребёнок маленьким человеком или нет. Точность – это характеристика понятия, содержание которого хорошо известно. Если существует хотя бы один плохо известный признак, то понятие неточно. Примером неточного понятия также может являться понятие «маленький человек», т. к. признак «маленький» непонятен, т. е. неизвестно, идёт ли речь о росте, возрасте или социальном положении. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ Пары понятий могут находиться в определённых отношениях. Эти отношения обуславливаются совместимостью или несовместимостью их содержаний и объёмов. Два понятия называются сравнимыми, если их содержание имеет хотя бы один общий собственный признак. В противном случае понятия называют несравнимыми. Например, понятия «стол» и «человек» сравнимы, т. к. и человек, и стол обладают массой, а понятия «бегун» и «бег» несравнимы, т. к. у них нет общих признаков в силу принадлежности их к разным классам явлений (слово «бег» обозначает процесс, а слово «бегун» – человека, этот процесс осуществляющего). Требование того, чтобы общие признаки были собственными, является существенным, т. к. если рассматривать и общие, и относительные признаки, то таковые найдутся у любой пары понятий. К примеру, относительный признак, поименованный каким-либо словом, принадлежит содержаниям всех без исключения понятий. Отношения между сравнимыми понятиями удобно изображать с помощью диаграмм Эйлера. На диаграмме Эйлера объём понятия изображается замкнутой плоской геометрической фигурой, чаще всего кругом (поэтому говорят о кругах Эйлера). Предмет, входящий в объём рассматриваемого понятия, изображается точкой внутри круга, а предмет, не входящий в объём понятия, – точкой вне круга (рис. 2). Сравнимые понятия, в свою очередь, делятся на совместимые и несовместимые. Совместимыми называются понятия, объём которых содержит хотя бы один общий предмет. Пара совместимых понятий может находиться в одном из трёх типов отношении: в отношении пересечения, отношении подчинения и отношении равенства. 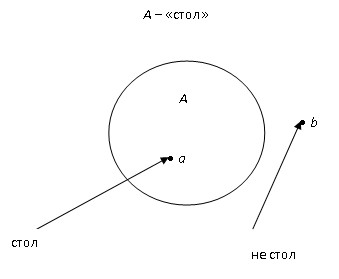  Рис. 2. Пример диаграммы Эйлера 1. Отношение пересечения. Если мы имеем два понятия, содержание которых различно, но объёмы некоторыми своими частями совпадают, то такие два понятия находятся в отношении пересечения (скрещивающиеся). Возьмём два понятия, например А – писатели и В – учёные. В объёме понятия «писатели» заключается часть объёма понятия «учёные», ибо некоторые «писатели» суть учёные, и, с другой стороны, в объёме понятия «учёные» заключается некоторая часть объёма понятия «писатели», ибо некоторые из учёных суть писатели. Это мы могли бы изобразить при помощи схемы на рис. 3. 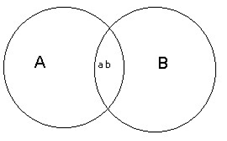  Рис. 3. Отношение перечисления Так как та часть объёма понятия «писатели», которая состоит из учёных, и та часть объёма понятия «учёные», которая состоит из писателей, логически между собой равны, то символически их можно представить равными частями двух кругов, которые при наложении могли бы совпасть. Поэтому схемой скрещивающихся понятий могут служить два скрещивающихся круга, причём круги символизируют объёмы данных понятий, а место их скрещивания – совпадающие, логически равные части этих объёмов. Другой пример – прямоугольные фигуры и параллелограммы, ибо некоторые прямоугольные фигуры суть параллелограммы и некоторые параллелограммы суть прямоугольные фигуры. 2. Отношение подчинения. Это отношение мы имеем в том случае, когда одно понятие относится к другому, как вид к своему роду, когда одно понятие входит в объём другого как часть его объема. Для примера возьмём понятие «дерево» (А) и понятие «берёза» (В). Последнее понятие входит в объём первого. (Символ подчинения понятий изображен на рис. 4.) Другие примеры: духовная деятельность, ощущение вкуса, человек, маЛекциятик. Понятие А в этом случае называется родовым по отношению к В (род), а понятие В – видовым по отношению к А (вид). 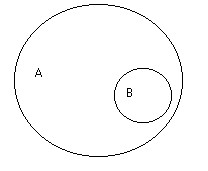  Рис . 4 Отношение подчинения 3. Отношение равенства. Для разъяснения этого отношения возьмём два понятия: «английский народ» и «первые мореплаватели в мире». Когда мы произносим слова «английский народ» и при этом имеем в уме понятие «английский народ», мы думаем об англичанах. Когда мы произносим слова «первые мореплаватели», мы также думаем об англичанах; следовательно, объём этих двух понятий один и тот же. Раскроем теперь содержание этих понятий. В понятии «английский народ» мы мыслим известное политическое устройство, известную территорию, известную культуру и т. д., в понятии же «первые мореплаватели» – известное искусство в постройке кораблей и управлении ими, известное развитие морской торговли, многочисленность флота и т. д.; следовательно, содержание этих понятий различно. Если у нас есть два понятия с различным содержанием, но одинаковым объёмом, то такие понятия называются «равнозначащими». Другие примеры: христианин – крещёный, органический – смертный, величайший писатель – автор «Войны и мира». Равнозначащие понятия можно символизировать при помощи двух кругов, сливающихся в один, подобно тому как сливаются объёмы указанных понятий; различие же содержания символизируется двумя различными буквами, стоящими в этом круге (рис. 5). 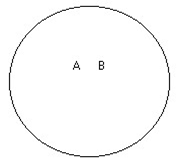  Рис. 5 Отношение равенства Несовместимые понятия также бывают трёх типов или находятся в одном из трёх типов отношений. Это отношения соподчинения, противоположности и противоречия. 1. Отношение соподчинения. Этот тип отношения мы имеем в том случае, если в объём одного и того же более широкого понятия входят два или несколько одинаково подчинённых ему низших понятий. Эти низшие понятия называются соподчинёнными (координированными). Например, мужество В, умеренность С, добродетель А. Оба первых понятия входят в объём последнего (рис. 6). 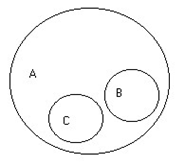  Рис. 6. Отношение соподчинения 2. Отношение противоположности. Если мы возьмём объём какого-нибудь понятия и будем распределять по степени сходства виды, входящие в него таким образом, что после каждого вида мы будем брать следующий, наименее от него отличный, то в конце концов из этих понятий-видов получится ряд, в котором первый и последний члены очень сильно отличаются друг от друга. Эти-то два понятия, первое и последнее, во взятом нами ряде видов находятся в отношении противности или противоположности. Будем, например, указанным способом распределять виды понятия «цвет». В его объём входят различные оттенки всевозможных цветов: красного, зелёного, чёрного, белого, серого и т. п. Если мы указанным выше способом будем размещать виды в ряд по мере их сходства, то можем получить приблизительно следующий ряд: белый, беловатый, светло-серый, серый, темно-серый, черноватый, чёрный. Как видно из этого, наибольшее различие здесь между понятиями «белый» и «чёрный»; они-то и суть противоположные, или противные, понятия. Итак, понятия, входящие в один и тот же объём, но очень отличающиеся друг от друга, называются противоположными. Схема: в круге, символизирующем объём какого-нибудь понятия, двумя линиями отделены два крайних отрезка, один против другого (рис. 7). 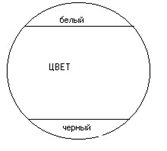  Рис. 7. Отношение противоположности Другие примеры: добрый, злой; высокий, низкий; красивый, уродливый; громкий, тихий; глубокий, мелкий. Надо заметить, что не все понятия имеют противоречащие им понятия. Например, понятие «голубой» не имеет противного ему понятия. 3. Отношение противоречия. Если мы имеем какое-нибудь понятие А и другое понятие В, относительно которого известно только то, что оно не есть А, то такие понятия называются противоречащими. Например, понятия «белый» и «небелый» суть понятия противоречащие. Итак, два термина, из которых один получен путём прибавления отрицательной частицы не к другому, относятся между собой как противоречащие. Символически отношение между противоречащими понятиями выражается следующим образом (рис. 8). 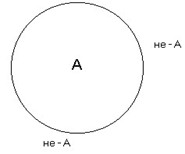  Рис. 8. Отношение противоречия Кругом символизируется какое-нибудь одно понятие А, и вне его ставится другое понятие В, которое есть не-А, причём это понятие В может быть поставлено где угодно, лишь бы не внутри круга, не в его объёме; это второе понятие по своим свойствам называется понятием отрицательным, или нёопредёленным. Если мы возьмём для сравнения два понятия противоположные и два противоречащие: белый – чёрный (противоположные); белый – небелый (противоречащие), – то мы можем наглядно убедиться, что разница между этими двумя логическими отношениями огромная: тогда как второй член первой пары (чёрный) имеет вполне определённое содержание, которое можно представить, второй член второй пары (небелый) такого определённого содержания не имеет. Его содержание отличается неопределённостью, т. е., употребляя слово «небелый», мы можем под ним понимать и красный, и зелёный, и синий, и даже большой, красивый, добрый и т. п. ОПЕРАЦИИ НАД ПОНЯТИЯМИ Логической операцией (или просто операцией) называется последовательность логических действий, в результате которых из исходных логических объектов образуются новые объекты. Если речь идёт об операциях над понятиями, то логическими объектами, очевидно, являются понятия. К основным операциям над понятиями относят следующие операции: 1) обобщение понятий; 2) ограничение понятий; 3) деление понятий; 4) определение понятий. Некоторые логики определение понятий не считают логической операцией, поскольку в результате определения не образуется нового понятия, но тем не менее традиционно определение считают операцией. Обобщение понятия Это логическая операция, состоящая в отбрасывании некоторых признаков из содержания исходного понятия, в результате которой из исходного понятия образуется новое понятие с более бедным содержанием и большим объёмом по сравнению с исходным понятием. Например, обобщением понятия «такса» будет понятие «собака», обобщением понятия «собака» будет понятие «животное» и т. д. Пределом обобщения будут наиболее широкие по объёму понятия, называемые категориями, у которых нет содержания, поскольку невозможно указать их признаки. Примеры категорий: бытие, пространство, время, жизнь, движение, взаимодействие и т. п. Ограничение понятия Ограничение понятия – логическая операция, состоящая в добавлении некоторых признаков к содержанию исходного понятия, в результате которой из исходного понятия образуется новое понятие с более богатым содержанием и меньшим объёмом по сравнению с исходным понятием. Например, ограничением понятия «автомобиль» будет понятие «легковой автомобиль», которое получилось из исходного добавлением к содержанию понятия «автомобиль» признаков, характеризующих только легковые автомобили. Неверно было бы думать, что понятие «легковой автомобиль» получается добавлением к содержанию понятия «автомобиль» признака «легковой». Слово «легковой» в данном случае обозначает не признак, а совокупность признаков, таких, как «вес автомобиля не более 3 т», «объём двигателя не более 3,5 л», «максимальное число перевозимых пассажиров не более 7» и т. д. (цифры взяты условно). Ограничением понятия «легковой автомобиль» может служить понятие «легковой автомобиль марки «мерседес», ограничением последнего понятия может служить понятие «Голубая акула», личное имя мерседеса какого-нибудь арабского шейха. Таким образом, пределом ограничения являются единичные понятия, поскольку дальнейшее уменьшение объёма понятия невозможно – остался только один предмет. Дальше можно только расчленять предмет, но это уже не будет ограничением понятия. Следует ясно представлять себе различие между родо-видовым отношением и отношением части к целому. Для родо-видовых отношений выполняется принцип: всё то, что можно сказать о роде, будет верно и для вида. Для отношения части к целому этот принцип не выполняется: далеко не всё, что можно сказать о целом, будет верно и для его частей. Например, берёза есть вид дерева, поэтому всё, что можно сказать о дереве вообще, будет верно и для берёзы. Но, скажем, ствол – это часть дерева, и то, что можно сказать о дереве, не всегда будет верно для ствола. Например, можно сказать: «Приятно в жаркий полдень отдохнуть в тени дерева». Но едва ли кто-нибудь скажет: «Приятно в жаркий полдень отдохнуть в тени ствола». Деление понятия Задача деления заключается в том, чтобы указать все виды, совокупность которых составляет объём данного понятия. Так, например, понятие «треугольник» мы могли делить следующим образом. Треугольник (А): прямоугольный (B) остроугольный (C) тупоугольный (D) У нас было понятие «треугольник» (А), и мы перечислили все частные понятия: В, С и D, – входящие в объём этого более общего понятия, которое относится к ним как род к своим видам. То понятие, объём которого мы раскрываем, называется делимым, а те виды, которые получаются от деления, называются членами деления. Когда мы производим деление рода на виды, то мы обращаем внимание на те признаки, которыми обладают одни виды и не обладают другие. Тот признак, который даёт нам возможность разделить род на виды, называется основанием деления. Основанием приведённого выше деления понятия «треугольник» была величина углов в треугольнике. Но можно это же самое понятие делить по какому-нибудь другому основанию (например, положить в основание деления отношение сторон треугольника по величине). Тогда деление представится в следующем виде. Треугольник (A): равносторонний (B); равнобедренный (C); разносторонний (D). Процесс несколько усложняется, если полученные от деления виды в свою очередь делить на подвиды (этот процесс называется подразделением). Так, например, вид понятия «треугольник» тупоугольный треугольник или какой-нибудь другой можно в свою очередь подразделить на подвиды: равнобедренный и разносторонний. Разумеется, деление и подразделение будут относиться к одному понятию «дихотомия». В процессе деления иногда употребляется приём, который называется дихотомией, который заключается в делении данного понятия А на противоречащие понятия В и не-В. Возьмем какое-нибудь понятие, которое нам надо разделить, например понятие «человек». Выделяем в одну группу какой-нибудь из видов, заключающихся в этом понятии, например вид «славянин», а в другую группу «не-славянин» относим все прочие виды. Затем с этим вторым отрицательным понятием поступаем точно таким же образом: подразделяем понятие «не-славянин» на две группы; в одну из них относим, например, подвид «германец», а в другую – все прочие остающиеся подвиды, соединяя их в одно понятие «не-германец»; затем с этим понятием поступаем точно так же, как и с предыдущим, и продолжаем наше деление до тех пор, пока оно не окажется исчерпанным. Человек: − славянин; − не-славянин; − германец; − не-германец и т. д. Этот приём имеет тот недостаток, что оставляет каждый раз крайне неопределённой часть объёма делимого понятия, именно ту часть, которая обозначается частицей не, но, с другой стороны, значительно облегчает сам процесс деления, потому что придаёт ему исчерпывающий характер, почему его иногда называют исчерпывающим делением. Что оно имеет исчерпывающий характер, можно объяснить при помощи следующего примера. Если мы разделим всех обитателей Европы и Азии на расы – белую и жёлтую, то может оказаться, что некоторые племена не подойдут ни под одну из этих рас, и мы будем не в состоянии поместить их в нашем делении, но этого не будет в том случае, если мы будем делить дихотомически. Обитатели земного шар: − белые; − не-белые; − желтые; − не-желтые. При таком делении всякое новое племя должно будет войти в последнюю группу, которая не будет ни белой, ни жёлтой. В этом заключаются преимущества дихотомического деления. Деление должно подчиняться следующим правилам: 1. Деление должно быть адекватно или соразмерно. Это значит, что если мы перечисляем по какому-нибудь основанию или принципу виды данного родового понятия, то мы должны точно перечислить все виды, не уменьшая и не увеличивая их количество, т. е. сумма видов должна равняться делимому роду. Если при делении мы не перечислим все виды, т. е. если эта сумма будет меньше, то у нас получится деление неполное; если же мы в объём делимого понятия введём виды, которые в нём на самом деле не содержатся, то у нас получится деление слишком обширное, т. е. указанная сумма будет больше. Например, положив в основание деления понятия «треугольник» величину его углов, мы могли бы получить такое деление: треугольник− остроугольный; − тупоугольный. Ясно, что это деление неполное, ибо здесь не хватает одного члена деления, потому что в объёме понятия «треугольник» находится ещё один вид, который при делении нами пропущен, а именно прямоугольный треугольник. Неполным было бы деление людей на порочных и добродетельных, деление научных теорий на истинные и ложные, потому что в этих делениях упускаются промежуточные ступени. Кроме людей порочных и добродетельных есть люди, о которых нельзя сказать, что они порочны, но нельзя также сказать, что они добродетельны; кроме истинных и ложных теорий существуют еще теории частью истинные и частью ложные. Обратная ошибка будет получаться в том случае, если мы, деля какое-либо понятие, вводим в его объём такой вид, который не входит в действительности в его объём. Если бы мы, например, разделили понятие «дерево» на «дуб», «ель», «фиалка», то очевидно, что вид «фиалка» относится к объёму совсем другого понятия и что при делении понятия «дерево» он попал в число членов его неправильно. 2. Члены деления должны исключать друг друга. Это требование станет ясным, если мы возьмём для примера следующее деление: книги: − и т. д. Это деление неправильно, ибо понятие, например, «французские книги» и понятие «словари» не исключают друг друга: книга может быть и французской, и словарём в одно и то же время. Или возьмём в пример также другое деление понятия книги: − полезные; − понятные; − интересные и т. д. Здесь один вид книг не исключает из своего объёма другие виды: полезная книга может быть в одно и то же время и понятной, и интересной. Ошибки как в первом, так и во втором из приведённых примеров деления произошли потому, что не было выдержано третье требование правильного деления. 3. Деление должно иметь одно основание. При делении понятий чаще всего повторяется ошибка, заключающаяся в том, что в процессе деления меняется основание деления. Произведём деление понятия «народы Европы»: − магометане; − христиане; − французы; − немцы и т. д. Это деление неправильно, ибо мы, взяв сначала основанием деления понятие «религия», затем меняем это основание на другое, именно на понятие «национальность». Или другой пример – прямоугольные фигуры: − треугольники; − параллелограммы; − прямоугольники; − многоугольники. Это деление также неправильно, так как у нас здесь скрещиваются такие различные основания деления, как число сторон, направление сторон, величина углов. Такое деление называется перекрёстным. Итак, третье условие правильности деления заключается в том, чтобы при последовательном перечислении видов делимого понятия было выдержано одно основание деления. Но следует заметить, что одно основание деления должно быть выдержано только при первом делении понятия; уже при вторичном делении, т. е. при подразделении, основание деления должно измениться. Так, например, если мы разделили понятие «треугольник», взяв основанием деления величину углов, на такие виды, как остроугольный, прямоугольный и тупоугольный, то, желая далее продолжать деление какого-нибудь из этих членов деления, мы уже должны основание деления изменить. Так, понятие «остроугольный треугольник» мы можем делить ещё далее, если возьмём основанием деления уже не величину углов, а отношение сторон по величине. Треугольник: 1) тупоугольный; 2) прямоугольный; 3) остроугольный; а) равносторонний; б) равнобедренный; в) разносторонний. 4. Деление должно быть непрерывным, т. е. при делении какого-либо понятия нужно переходить к ближайшему низшему роду, в противном случае будет получаться то, что называется скачком в делении. Если бы мы понятие «природа» разделили на животных, растения, минералы, то в этом делении был бы слишком внезапный переход от понятия «природа» к понятиям «минералы», «животные». Чтобы исправить ошибку, следует вставить между понятием «природа» и членами приведённого выше деления ещё два посредствующих звена, а именно: понятия «мир неорганический» и «мир органический». Тогда деление приняло бы следующий вид: природа: ♦ мир органический: − животные; − растения; ♦ мир неорганический: - минералы и проч. Определение понятия Когда мы произносим какое-либо слово, соответствующее известному понятию, и хотим сделать его понятным для всех, то мы должны раскрыть содержание понятия, соответствующего указанному слову, а так как содержанием понятия называется совокупность его признаков, то раскрытие содержания понятия можно обозначить как перечисление признаков, присущих данному понятию. Какое-либо понятие А содержит признаки а, b, с, d; если мы перечислим эти признаки, то тем самым точно обозначим, раскроем содержание понятия А; это значит, другими словами, что мы определим его. Следует заметить, что не все понятия могут быть определены. Понятия по своему содержанию бывают весьма различны: содержание одних понятий больше, других – меньше. Такие понятия, которые имеют сложное содержание, т. е. имеют много признаков, могут быть определены. Но есть понятия, которые имеют настолько простое содержание, что не могут быть определены, потому что, как было сказано, для определения необходимо раскрытие содержания понятия; если же содержание понятия не может быть раскрыто, то оно не может быть и определено. Такие понятия называются простыми. Например, понятие «пунцовый цвет» не подлежит определению: цвет этот нужно видеть, чтобы знать, что он такое. Все определения, которые мы попытались бы дать в данном случае, были бы ложными в логическом отношении. Точно так же определять, что такое «тон известной высоты», бесполезно; это понимается непосредственным восприятием этого тона. Сюда же относятся такие понятия, как, например, «равенство», «тождество», «тяжесть», «протяжение», «сознание» и т. п. Точно так же не могут быть определяемы индивидуальные понятия, потому что при их определении пришлось бы перечислить бесконечное множество признаков. Например, этот бриллиант. Итак, определить то или иное понятие значит перечислить его признаки. Но это представляется иногда задачей трудной, потому что количество признаков того или другого понятия может быть очень велико, поэтому перечислить даже большинство этих признаков не окажется возможным. Если бы, например, определяя понятие «прямоугольник», мы сказали, что прямоугольник есть геометрическая фигура, плоская, ограниченная прямыми линиями, четырёхугольная, с прямыми углами и т. д., то это определение было бы правильно, но практически оно неудобно, потому что перечисляется целый ряд признаков. Вследствие этого принят другой способ определения понятий, который имеет целью избежать полного перечисления признаков. Он заключается в следующем. Дадим определение прямоугольника. Для этой цели мы воспользуемся понятием «параллелограмм». Когда мы употребляем термин «параллелограмм», то под ним мы понимаем или прямоугольник, или ромб, или квадрат. Зная это, мы не будем говорить, что прямоугольник есть геометрическая фигура, плоская, ограниченная прямыми линиями, четырёхугольная и т. д., а просто скажем, что это есть параллелограмм, в котором все углы прямые, ибо всякий под словом «параллелограмм» разумеет геометрическую фигуру, ограниченную четырьмя прямыми, попарно параллельными линиями; прибавляя, что все углы фигуры прямые, мы окончательно завершаем определение ее именно тем, что мы отличаем прямоугольник от ромба и от квадрата, которые тоже суть параллелограммы. Таким образом, определяя понятие «прямоугольник», мы указали род данного понятия (параллелограмм) и присоединили к нему его видовое различие (четыре прямых угла), отличающее его от других видов, входящих в тот же род, т. е. от ромба и квадрата. Руководствуясь тем же правилом, мы скажем, что ромб есть параллелограмм, в котором все стороны равны, а квадрат есть параллелограмм, в котором стороны и углы равны. Итак, определение заключается в указании рода данного понятия с присоединением его видового различия. Это в логике принято обозначать при помощи формулы «Definitio fit per genus et differentiam specificam», т. е. определение совершается при помощи рода и видового различия. Если нам нужно определить какое-либо понятие, то мы выражаем наше определение при помощи суждения, содержащего подлежащее и сказуемое. Подлежащее этого суждения называется определяемым (definiendum), сказуемое называется определяющим (definiens). Эти термины важны потому, что благодаря им мы можем указать те правила, при соблюдении которых получается правильное определение. Таких правил четыре: Определение должно быть соразмерным, таким, в котором объёмы определяемого и определяющего тождественны, т. е. одинаково велики. Если правило это нарушено, то определение неадекватно, или несоразмерно. В таком случае определение делается или слишком широким, или слишком узким, т. е. объём определяющего становится слишком широким или слишком узким в сравнении с объёмом определяемого. Возьмём в пример определение лошади. Если сказать, что лошадь есть домашнее животное, то это определение будет слишком широким; в нём объём определяющего будет более широким, чем объём определяемого понятия (в объём понятия домашнего животного, кроме лошади, входят ещё коровы, собаки и т. п.). Относительно такого определения можно также сказать, что в него не входит указание существенного признака данного понятия. Если в определении опущены существенные признаки понятия, тогда оно окажется слишком широким, как в только что приведённом примере. Возьмём определение, которое погрешает в противоположном направлении. Если бы мы сказали, что треугольник есть плоская прямолинейная фигура, имеющая три «равные стороны», то это определение было бы слишком узким. В нём объём определяющего понятия меньше объёма определяемого понятия, а именно: в объём определяющего понятия входят только равносторонние треугольники, а в объём определяемого понятия входят как равносторонние, так и неравносторонние треугольники. Определение не должно делать круга. Это правило требует, чтобы определяемое понятие не определялось посредством понятия, которое само делается понятным только посредством определяемого. Возьмём, например, определение «вращение есть движение вокруг оси». Это определение понятия «вращение» посредством понятия «ось» делает круг, ибо само понятие «ось» определяется только через понятие «вращение» (как известно, ось – это прямая, вокруг которой происходит вращение). Таким образом, ясно, что в нашем определении получается круг: понятие «вращение» определяется посредством понятия «ось», а понятие «ось» – посредством понятия «вращение». В определении определяющее и определяемое должны быть двумя различными и притом самостоятельными понятиями. Если это не соблюдается, то получается ошибка, которая называется тавтологией, а именно: в определении получается только повторение того же слова, т. е. употребляются слова, имеющие то же самое значение, например: свет есть то, чему присущ свет; величина есть то, что способно уменьшаться и увеличиваться. Последнее определение представляет собой тавтологию, потому что уменьшение есть убавление величины, увеличение же есть прибавление величины, а потому, если мы определяем величину посредством того, что способно увеличиваться или уменьшаться, то очевидно, что в определяющем понятии содержится определяемое понятие. Определение не должно быть отрицательным, оно должно указывать признаки, присущие данному понятию, а не чуждые ему, ибо эти последние для нас неважны и, кроме того, их можно указать очень много. Например, возьмём определение «театр есть здание, не служащее для жилья». Если А будет здание, служащее для жилья, то не-А, или зданий, не служащих для жилья, будет бесчисленное множество. Таким образом, это определение делается для нас непригодным. К числу определений, которые вследствие своего отрицательного характера непригодны, нужно отнести следующие: «жидкость есть то, что не твердо и не газообразно», «точка есть то, что не имеет частей и не имеет никакой величины». Отрицательные определения не раскрывают содержания понятия, они оставляют содержание понятия неопределённым. Поэтому отрицательные определения не отвечают главной цели определения – раскрыть содержание определяемого понятия, сделать содержание понятия определённым. Отрицательные определения могут быть употребляемы только тогда, когда определяемое понятие имеет отрицательный характер, например: «чужестранец – это человек, не принадлежащий к данной стране» и т. д. Определение должно быть ясным, т. е. в определении нельзя пользоваться выражениями двусмысленными, метафорическими и вообще малопонятными. Нарушение этого правила приводит к попытке сделать понятным неизвестное через посредство ещё менее известного. Например, выражения «архитектура есть застывшая музыка» и «нужда есть мать изобретения» есть образные выражения, которые не объясняют значения термина. Если же сказать, что «эксцентричность есть своеобразная идиосинкразия», то мы непонятное пытаемся объяснить посредством непонятного же. Приёмы, заменяющие определения Итак, чтобы наши определения были точны, они должны удовлетворять указанным четырём правилам. Но не следует думать, что все наши понятия могут быть всегда определяемы указанными способами. Есть случаи, когда приходится знакомиться с содержанием понятия не посредством определения, а иными способами. Можно указать следующие способы, заменяющие определение: Указание. Если, например, мы кого-нибудь желаем познакомить с тем, что такое тот или другой цвет, звук и т. п., то сделать это можно только в том случае, если привести его в соприкосновение с данным цветом, звуком и т. п., т. е. заставить его воспринимать то, с чем мы желаем его ознакомить. Такой способ ознакомления с известным понятием называется указанием. Указание употребляется во всех случаях, когда нам приходится знакомить кого-нибудь с предметами нёпосредственного восприятия. Описание употребляется при ознакомлении с индивидуальными предметами или при ознакомлении со свойствами, принадлежащими какой-либо вещи. В таком случае приводятся возможно точно и полно признаки этой вещи, например: описание Днепра у Гоголя, Рейнского водопада у Карамзина и т. п. В ботанике описываются строение того или иного цветка, процесс опыления и т. п., в химии описывается та или иная реакция. Характеристика приводит выдающиеся признаки какого-либо предмета или явления. Если нам нужно познакомить кого-нибудь с тем, что такое воображение построительное и воображение воспроизводящее, то мы вместо определения можем указать на какую-нибудь существенную черту, присущую тому или другому виду воображения, например говорим, что для построительного воображения существенным является новизна сочетания, а для воспроизводящего – точность. Какое-нибудь свойство является характерным для того или другого лица: для воина – мужество, для врача – гуманность и т. п. Характерной особенностью семейства крестоцветных растений являются цветы с четырьмя листочками чашечки и четырьмя лепестками венчика, расположенными крест-накрест, с двумя короткими и четырьмя длинными тычинками. Сравнение употребляется в том случае, когда мы знакомимся с тем или иным понятием при помощи сравнения его с другими понятиями, похожими на него. Мы можем дать понятие о теплопроводности какого-либо тела при помощи сравнения её со светопрозрачностью, например, если скажем, что теплопроводность по отношению к тепловым лучам есть то же самое, что прозрачность по отношению к световым лучам. Сравнение употребляется главным образом тогда, когда одно понятие уясняется при помощи другого понятия, более ясного, например, когда какое-либо абстрактное понятие уясняется при помощи конкретного, например: жизнь есть школа опыта, право есть воплощение, нравственной идеи, совесть есть внутренний суд. Различение употребляется в том случае, когда мы знакомим кого-нибудь с содержанием какого-либо понятия, указывая на то различие, которое существует между данным понятием и другими, например, если мы говорим, что энтузиазм отличается от фанатизма тем, что он вызывается чем-либо благородным и не переходит за пределы умеренности. |
