Пример решения задач по эконометрике. Практикум Решение типовых задач Задача Имеются выборочные данные (табл. 1) показателей среднедушевой денежный доход
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Практикум Решение типовых задач Задача 2.1. Имеются выборочные данные (табл. 1) показателей «среднедушевой денежный доход» (х, руб.) и «среднедушевой оборот розничной торговли» (y, руб.). Найти коэффициент парной корреляции между показателями; коэффициент детерминации; определить статистическую значимость коэффициентов; построить доверительный интервал для коэффициента корреляции. Таблица 1
Решение. Объем выборки n = 16. 1) Коэффициент парной корреляции найдем по формуле  . .Составим расчетную таблицу (расчеты выполнены в Excel) (см. табл. 2). Средние значения признаков равны Таблица 2 Расчетная таблица
Парный коэффициент корреляции равен Величина коэффициента корреляции, находящаяся в пределах от 0,7 до 0,95 свидетельствует о тесной связи (близкой к умеренной) между среднедушевым денежным доходом и среднедушевым оборотом розничной торговли. Поскольку значение коэффициента парной корреляции положительно, эта связь прямая. 2) Коэффициент детерминации Показывает, что на 49,98% изменение оборота розничной торговли объясняется изменениями денежных доходов населения. Оставшиеся 50,02% приходятся на другие факторы, не включенные в модель. 3) Статистическую значимость коэффициента корреляции проверим с помощью критерия Стьюдента. Найдем 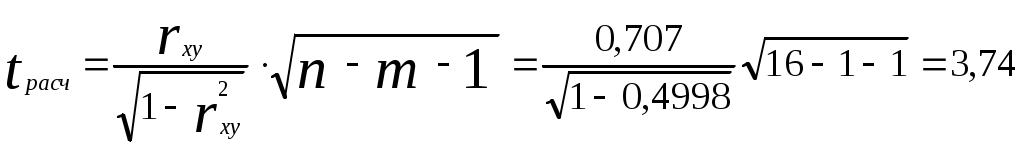 (m = 1). (m = 1).Табличное значение t-критерия Стьюдента при уровне значимости α = 0,05 и числе степеней свободы df = n - m - 1 = 16 - 1 - 1 = 14 составляет tтабл = 2,14. (табличное значение критерия найдено с помощью встроенной функции Excel «СТЬЮДРАСПОБР»). Так как |tрасч| > tтабл (3,74 > 2,14) , значение коэффициента корреляции статистически значимо. Статистическая значимость парного коэффициента корреляции подтверждает тесную связь (близкую к умеренной) между среднедушевым денежным доходом и среднедушевым оборотом розничной торговли. 4) Статистическую значимость коэффициента детерминации проверим с помощью критерия Фишера. Найдем  Табличное значение F-критерия Фишера при уровне значимости α = 0,05 и числах степеней свободы df1 = m = 1 и df2 = n - m - 1 = 16 - 1 - 1 = 14 составляет Fтабл = 4,60. (табличное значение критерия найдено с помощью встроенной функции Excel «FРАСПОБР»). Так как Fрасч > Fтабл (13,99 > 4,60), коэффициент детерминации признается статистически значимым. 5) Построим интервальную оценку парного коэффициента корреляции (доверительный интервал) Стандартная ошибка коэффициента корреляции равна  . .Доверительный интервал имеет вид или Т.е. с вероятностью (надежностью) γ = 1 – α = 1 – 0,05 = 0,95 значение коэффициента корреляции генеральной совокупности находится внутри интервала (0,302; 1,112). Границы доверительного интервала имеют одинаковые знаки, что подтверждает вывод критерия Стьюдента о статистической значимости коэффициента парной корреляции. Задача 2.2. (Пример применения z-преобразования Фишера для построения доверительного интервала коэффициента корреляции). По двумерной выборке значений признаков x и y объема n = 8 найден коэффициент корреляции rxy = - 0,462 (l = 1) и для α = 0,05, т.е. rxy считается незначимым. Но поскольку n = 8 мало, необходимо подтвердить вывод о статистической незначимости построением доверительного интервала для rxy при γ = 0,95. Найдем интервальную оценку для z. По таблице z‑преобразования Фишера для rxy = - 0,462 , учитывая, что z'(- r) = - z'(r) ,будем иметь z'(- 0,462) = - z'(0,462) = - 0,497. (В данной работе табличное значение z'(- 0,462) найдено с помощью встроенной функции Excel «ФИШЕР».) По таблице нормального закона распределения из условия Ф(tγ) = 0,95 найдем tγ = 1,96. Тогда, согласно интервальная оценка z имеет вид: - 1,477 ≤ z ≤ 0,483 . По таблице z-преобразования для zmin = - 1,477 и zmax = 0,483 найдем соответственно rmin = - 0,90 и rmax = 0,45 (в данной работе значения rmin и rmax найдены с помощью встроенной функции Excel «ФИШЕРОБР»). Доверительный интервал для парного коэффициента корреляции имеет вид - 0,90 ≤ rxy ≤0,45 . Полученная интервальная оценка подтверждает вывод о незначимости парного коэффициента корреляции rxy , т.к. ноль находится внутри доверительного интервала (коэффициент корреляции не может одновременно принимать положительное и отрицательное значение). Задача 2.3. Для выяснения зависимости объема реализации продукции (y, млн руб.), расходов на рекламу (х1, тыс. руб.) и цены единицы продукции (х2, руб.) обследованы 20 организаций торговли. В результате обследования получены следующие данные: Таблица 3
Требуется найти: 1) матрицу выборочных парных коэффициентов корреляции; 2) выборочный частный коэффициент корреляции между объемом реализации продукции (y) и расходами на рекламу (х1); выборочный частный коэффициент корреляции между объемом реализации продукции (y) и ценой единицы продукции (х2). 3) выборочный множественный коэффициент корреляции между объемом реализации продукции (y) и расходами на рекламу (х1) и ценой единицы продукции (х2); коэффициент детерминации. |
