|
|
КСП для 8; 10 класса. Предел функции в точке и на бесконечности
Раздел:
|
10.3В Предел функции и непрерывность
|
ФИО педагога
|
Лаган Н.Д.
|
Дата: 2.02.22
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Предел функции в точке и на бесконечности
|
Цели обучения в соответствии
с учебной программой
|
10.4.1.8 - знать определение предела функции в точке и вычислять его;
10.4.1.9 - знать определение предела функции на бесконечности и вычислять его;
|
Цели урока
|
Понимать определение предела функции в точке и применять его при решении задач
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
2 мин
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
8мин
|
Ознакомление с теорией предела функции. п.36
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом 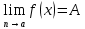 . .
Вычислим предел: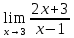
Подставляем вместо х = 3.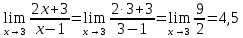
Заметим, что предел числа равен самому числу.
Определение: Если число А1 есть предел функции 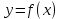 при х, стремящемся к числу а так, что х принимает только значения меньшие числа а, то число А1 называется левым пределом функции при х, стремящемся к числу а так, что х принимает только значения меньшие числа а, то число А1 называется левым пределом функции 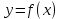 в точке а. в точке а. 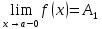 . .
Определение: Если число А2 есть предел функции 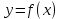 при х, стремящемся к числу а так, что х принимает только значения большие числа а, то число А2 называется правым пределом функции при х, стремящемся к числу а так, что х принимает только значения большие числа а, то число А2 называется правым пределом функции 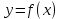 в точке а. в точке а. 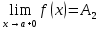 . .
Теорема 1: Если существует пределы функций 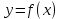 и и 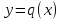 при х, стремящемся к числу а, то существует предел их суммы, равный сумме пределов этих функций. при х, стремящемся к числу а, то существует предел их суммы, равный сумме пределов этих функций.
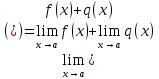
Теорема 2: Если существует пределы функций 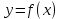 и и 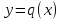 при х, стремящемся к числу а, то существует предел их произведения, равный произведению пределов этих функций. при х, стремящемся к числу а, то существует предел их произведения, равный произведению пределов этих функций.
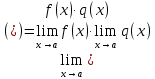
Теорема 3: Если существует пределы функций 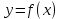 и и 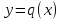 при х, стремящемся к числу а и при х, стремящемся к числу а и 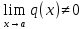 , то существует предел их отношения, равный отношению пределов этих функций. , то существует предел их отношения, равный отношению пределов этих функций.
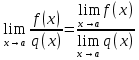
Определение. Функция 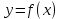 называется бесконечно малой при называется бесконечно малой при 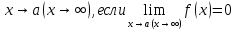 . .
Определение. Функция 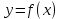 называется бесконечно большой при называется бесконечно большой при 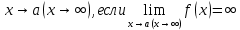 . .
При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
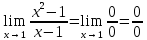
Основные виды неопределенностей: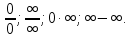
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, помножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
Пример: Вычислим предел.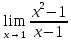
Разложим числитель на множители: 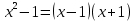
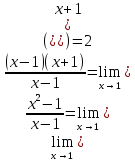
|
работают с учебником;
|
|
учебник
|
Парная работа
|
Парная работа.
№36.3; №36.9(1,3)
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
Индивидуальная работа.Задания формативного оценивания.
№36.10(1)
|
работают самостоятельно
|
самопроверка
|
|
Рефлекция
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
|
Обобщают изученный материал.
Делают вывод.
Оценивают свою работу на уроке(самооценивание) о
|
Оценка учителя.
|
|
Домашнее задание
|
§36 №36.4; №36.9(2, 4)
|
Записывают в дневники домашнее задание.
|
|
Учебник Абылкасымова А.Е. 2019
|
Раздел:
|
|
ФИО педагога
|
|
Дата: 18.01.22
|
|
Класс: 10 б
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Предел функции в точке и на бесконечности
|
Цели обучения в соответствии
с учебной программой
|
10.3.1.7 - знать определение предела функции в точке и на бесконечности;
|
Цели урока
|
Понимать определение предела функции в точке и применять его при решении задач
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
2 мин
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
8мин
|
Ознакомление с теорией предела функции.
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. п.12 с.77 Пример 1,2.
При вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, помножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
|
работают с учебником;
|
|
учебник
|
Парная работа 11мин
|
Парная работа.
№12.1
№ 12.4
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
7мин
|
№ 12.6 (а)
|
работают самостоятельно
|
|
|
Рефлекция
(3 мин)
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
|
Обобщают изученный материал.
Делают вывод.
Оценивают свою работу на уроке(самооценивание) о
|
Оценка учителя.
|
|
Домашнее задание
1 мин
|
п.12 №12.2,онлайн мектеп
|
Записывают в дневники домашнее задание.
|
|
| |
|
|
 Скачать 437.19 Kb.
Скачать 437.19 Kb.