Учебное пособие для студентов высших учебных заведений очного и заочного обучения
 Скачать 1.22 Mb. Скачать 1.22 Mb.
|
|
Министерство сельского хозяйства Российской Федерации Федеральное государственное бюджетное общеобразовательное учреждение высшего образования Иркутский государственный аграрный университет имени А.А. Ежевского А.В. Шистеев КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Учебное пособие для студентов высших учебных заведений очного и заочного обучения направления подготовки: 35.03.06 «Агроинженерия» 23.03.03 «Эксплуатация транспортно-технологических машин и комплексов» Уровень бакалавриата 44.03.04 «Профессиональное обучение»  УДК 531.01(075.8) Ш 647 Ш 647 Шистеев А.В. Курс теоретической механики: учеб. пособие. – п. Молодежный: Издательство Иркутского государственного аграрного университета имени А.А. Ежевского, 2019. – 118 с.: ил Рекомендовано к изданию учебно-методическим советом ФГБОУ ВО Иркутский государственный аграрный университет имени А.А. Ежевского Рецензенты Т.И. Кривцова, к.т.н., доцент кафедры «Автомобильный транспорт» ФГБОУ ВО Иркутский национально-исследовательский технический университет; А.В. Кузьмин, д.т.н., профессор кафедры «Технический сервис и общеинженерные дисциплины» ФГБОУ ВО Иркутский государственный аграрный университет имени А.А. Ежевского В учебном пособии даны материалы по основам теоретической механики, предложен краткий курс лекций и практических работ. Представлены методические рекомендации для успешного освоения студентами подразделов статики, кинематики и динамики, приводятся примеры решения задач. Учебное пособие предназначено студентов высших учебных заведений направлений подготовки 35.03.06 «Агроинженерия», 23.03.03 «Эксплуатация транспортно-технологических машин и комплексов», 44.03.04 «Профессиональное обучение», уровень бакалавриата. Пособие может быть полезным для широкого круга лиц, интересующихся данными теоретическими и практическими вопросами. © Шистеев А.В. © Издательство ФГБОУ ВО ИрГАУ имени А.А. Ежевского, 2019  СОДЕРЖАНИЕ
Введение Одним из самых существенных критериев успеха в современное время является конкурентоспособность выпускаемой продукции, а также работ и услуг, зависящих в свою очередь от качества проведенных расчетов на разных стадиях производственного проектирования. В связи с этим, изучение теоретической механики является одним из инструментов обеспечения необходимого уровня качества оказываемых работ, услуг или производимой продукции. Механика - (от греческого mechanike – это искусство построения машин) - наука о механическом движении материальных тел (об изменении с течением времени взаимного положения тел или частей этих тел в пространстве) и взаимодействиях между ними. Механика зародилась в глубокой древности. Например, строители египетских пирамид пользовались эмпирическими знаниями по механике. Знаменитый древнегреческий философ Аристотель (384 – 322 гг. до н.э.) уже знал закон сложения сил, приложенных в одной точке и направленных по одной прямой. Выдающийся ученый Архимед (287 – 212 гг. до н.э.) заложил основы статики, как точной науки. Во все времена теоретическая механика развивалась параллельно с развитием техники и ее достижения обеспечивали своевременный, а иногда идущий на опережение технический прогресс человечества и эта ее роль сохраняется и в современное время. В основе классической механики, современные положения которой приведены в настоящем пособии, лежат законы Ньютона, соответственно такими методами классической механики изучаются движения любых материальных тел (кроме микрочастиц), которые перемещаются в пространстве со скоростями, являющимися очень малыми по сравнению со скоростью света. Движения тел со скоростями, близкими к скорости света, рассматриваются в теории относительности, а движение микрочастиц - в квантовой механике. На протяжении многих тысяч лет законы механики используются человеком для расчетов машин, механизмов, строительных сооружений, транспортных средств, космических летательных аппаратов и т.д. Иными словами теоретическая механика – это математика, приложенная к законам равновесия и движения тел; наука о силе и сопротивлении ей, своеобразное искусство применять силу к делу и строить машины, наука выгодного приспособления сил, как пишет в своем словаре Владимир Иванович Даль в середине XIX века. Огромный вклад в развитие механики внесли и наши многочисленные отечественные ученые, такие как: Ломоносов М.В., Леонард Эйлер, Остроградский М.В., Чебышев П.Л., Ковалевская С.В., Ляпунов А.М., Мещерский И.В., Крылов А.Н., Жуковский Н.Е., Седов Л.И., Ишлинский А.Ю., Яненко Н.Н., Антонец Д.А. и многие другие. Предмет теоретической механики является одним из самых важнейших при изучении фундаментальных общенаучных инженерных дисциплин и играет существенную роль при подготовке инженеров любых специальностей. На результатах теоретической механики базируются такие общеинженерные дисциплины как: сопротивление материалов, детали машин, теория механизмов и машин и многие другие. Раздел I. Статика Лекция 1 Введение в теоретическую механику. Основные понятия и аксиомы статики. Система сходящихся сил: сложение сходящихся сил (геометрический и аналитический способы), условия равновесия системы сходящихся сил на плоскости и в пространстве. Момент силы относительно точки (алгебраический и как вектор). Теорема Вариньона о моменте равнодействующей. Условие равновесия рычага. Момент силы относительно оси и его связь с моментом силы относительно точки на оси. Аналитические формулы момента силы относительно осей координат. Введение в теоретическую механику Теоретической механикой называется наука об общих законах механического движения и равновесия материальных твердых тел. Под механическим движением понимается изменение положения тела в пространстве относительно других тел с течением времени. Теоретическая механика – наука естественная. Ее основные понятия и законы имеют первоисточником непосредственные наблюдения и повседневный опыт человека. Поэтому теоретическая механика, как и все другие науки о законах развития природы, широко пользуется математическими методами исследования, а также методом абстракции, методами обобщения и формальной логики. Теоретическая механика подразделяется на три раздела: статику, кинематику, динамику. Основные понятия и аксиомы статики Статикой называется раздел теоретической механики, в котором излагается учение о силах и условиях равновесия твердых тел при действии на них сил. Под равновесием твердого тела понимается состояние его покоя или равномерного прямолинейного поступательного движения. Под твердым телом в теоретической механике понимается абсолютно твердое тело, то есть такое тело, геометрическая форма которого и размеры не изменяются ни при каких механических воздействиях со стороны других тел, а расстояние между двумя любыми его точками остается всегда постоянным. Механическим воздействием или взаимодействием тел называется такое воздействие, при котором пренебрегают изменениями в химической структуре тела и его физическом состоянии (нагревом, охлаждением и т.д.). Механическое воздействие может происходить как при соприкосновении тел, так и на расстоянии (притяжение, отталкивание). Сила – одно из основных понятий статики. Силой называется векторная величина, являющаяся количественной мерой механического взаимодействия тел. действие силы на тело определяется тремя факторами: модулем силы, направлением силы, точкой приложения силы. На чертежах сила, как и всякий вектор, изображается отрезком со стрелкой и обозначаются заглавными буквами латинского алфавита с черточкой над буквой (в книгах могут выделяться жирным шрифтом). Буква без черточки означает, что речь идет о модуле силы. Линией действия силы называется такая прямая, вдоль которой направлен вектор силы. Обычно на тела действует несколько сил. Совокупность всех сил, действующих на данное тело, называется системой сил. Если системы сил, приложены порознь к данному телу, но оказывают на него одинаковое действие, то они называются эквивалентными. Система сил, под действием которой свободное твердое тело находится в равновесии, называется уравновешенной или эквивалентной нулю. Если система сил может быть заменена одной силой (эквивалентна одной силе), то эту силу называют равнодействующей. Силу, которая при добавлении ее к данной системе сил образует вместе с нею систему сил эквивалентную нулю, называют уравновешивающей силой. Для системы сил, имеющей равнодействующую, уравновешивающая будет равна ей по модулю и направлена по линии действия равнодействующей в противоположную сторону. Различают силы сосредоточенные и распределенные. Сосредоточенной называют силу, приложенную к телу в какой-либо точке. Распределенными называют силы, действующие на все точки какого-либо объема тела или его поверхности, или некоторой части линии. Задаются эти силы интенсивностью q – величиной силы, приходящейся на единицу объема, площади, длины линии. При решении задач распределенные силы заменяют на сосредоточенные, поскольку все положения статики формулируются для сосредоточенных сил. По расположению различают следующие системы сил: сходящиеся на плоскости и в пространстве; как угодно расположенные (произвольные) на плоскости и в пространстве; системы пар на плоскости и в пространстве; системы параллельных сил на плоскости и в пространстве (это частные случаи произвольных систем сил). Сходящейся называется такая система сил, у которой линии действия всех сил пересекаются в одной точке. Произвольной называется система сил, у которой линии действия сил не пересекаются в одной точке. Научные положения статики базируются на пяти аксиомах (постулатах) – не требующих доказательства, так как их справедливость подтверждена многовековой практикой и наблюдениями за равновесием и движением тел. Далее приведем формулировки аксиом. Аксиома 1. Если на свободное твердое тело действуют 2 силы, то оно будет находится в равновесии только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в разные стороны. Аксиома 2. Действие данной системы сил на твердое не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Аксиома 3. При всяком действии одного тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. Заметим, что сила действия и противодействия уравновешенной системы сил не образуют, так как они приложены к разным телам. Аксиома 4 (аксиома параллелограмма). Равнодействующая двух сил, приложенных к твердому телу в одной точке под углом друг к другу, равна по модулю и направлению диагонали параллелограмма, построенного на этих силах, как на сторонах. Аксиома 5 (принцип отвердевания). Если какое-либо деформируемое твердое тело находится в равновесии под действием данной системы сил, то это состояние не нарушится и после, как это тело отвердеет, то есть станет абсолютно твердым. Эта аксиома позволяет получаемые в статике условия равновесия для абсолютно твердых тел применять для рассмотрения равновесия реальных (деформируемых) тел. Из первой и второй аксиом вытекает следствие: действие силы на тело не изменится от переноса точки ее приложения в любую другую точку тела. Это следствие касается равновесия тела. Если же речь идет о характере усилия (растяжение, сжатие), то оно не справедливо, так как от переноса точки приложения силы характер усилия изменяется. Система сходящихся сил. Сложение сходящихся сил. Сложить сходящиеся силы – это значит найти их равнодействующую. Существуют два способа сложения - геометрический и аналитический. Геометрический способ заключается в том, что из сил системы строят силовой многоугольник А, В, С,…, D, E, для чего силы, в масштабе, последовательно откладывают так, чтобы конец вектора предыдущей силы являлся началом вектора последующей силы. После отложения всех сил проводят замыкающую сторону многоугольника. Она дает и модуль, и направление равнодействующей R (Рисунок 1). 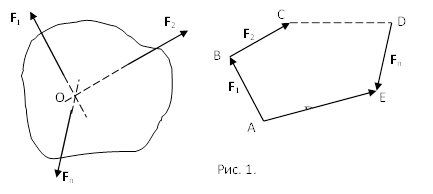 Рисунок 1 – Построение силового многоугольника При этом линия действия равнодействующей проходит через точку О пересечения сил системы. Необходимо отметить, что если конец вектора последней откладываемой силы придет в начальную точку А многоугольника (получится замкнутый многоугольник), то это будет значить, что равнодействующая равна нулю (замыкающей стороны у силового многоугольника нет). В качестве недостатков данного способа можно выделить недостаточную точность и большую трудоемкость выполнения. Аналитический способ сложения сходящихся сил дает точный результат и состоит в следующем. Сначала определяют проекции равнодействующей на оси координат, которые равны суммам проекций всех сил системы на соответствующие оси. 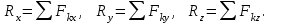 Затем определяют модуль равнодействующей: 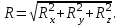 (1) (1)После чего определяют направление равнодействующей по направляющим косинусам: 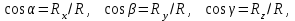 где 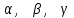 - этоуглы между равнодействующей и осями x, y, z соответственно. - этоуглы между равнодействующей и осями x, y, z соответственно. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
