|
|
1. Технологический процесс и его структура Технологическим процессом
3.1. Методы достижения заданной точности замыкающего звена в сборочной размерной цепи, их выбор.
На этапе проектирования машины достижение требуемой точности взаимного положения поверхностей деталей обеспечивается путем выявления и расчета сборочных размерных цепей.
Основные зависимости, используемые при расчете, сводятся к двум уравнениям:
1.Устанавливается соотношение м/у значениями допусков составляющих звеньев и замыкающего звена. При расчете на «max-min» Т∑ равен:
При расчете вероятностным методом используется уравнение (2)
где t – коэффициент риска, λi' – коэффициент относительного рассеяния каждого из составляющих звеньев (учитывает отклонение рассеивания всех звеньев от норм. закона). Для норм. закона λi'=1/9. Для закона, близкого к треугольному, λi'=1/6. Для равновероятностного распределения λi'=1/3.
2.Устанавливается расположение допуска замыкающего звена относительно его номинального размера. а) при расчете на «max-min» координата середины поля допуска рассчитывается:
(3)
б) при расчете вероятностным методом
(4)
где αi – коэффициент смещения центра рассеивания размера i-го звена относительно середины поля допуска Тi.
Чем короче размерная цепь и меньше сведений о фактических параметрах распределения размеров составных звеньев, тем меньше разница в результате расчета размерной цепи вероятностным методом и методом «max-min». Расчет многозвенных размерных цепей по уравнениям (1-4) часто приводит к тому, что получаемые допуска практически невыполнимы и не экономичны. Поэтому приходится расширять допуски: организацией селективной сборки; пригонкой компенсирующего звена; введением в размерную цепь дополнительного компенсирующего звена.
1. Сущность селективной сборки заключается в том, что детали, которые поступают на сборку, сортируются по их действительным размерам на несколько групп. Сборочная единица составляется из деталей, которые входят в одноименные группы, и точность сопряжения повышается во столько раз, на сколько групп разбивают исходный допуск (рис.2.1.1).
Применение селективной сборки ограничивается рядом условий. Одно из главных – примерно одинаковое количество деталей в каждой из размерных групп. Это осуществимо только в условиях крупносерийного и массового производства.
2. Метод пригонки. На одном из звеньев, которое выполняет роль компенсатора, оставляют припуск, необходимую часть которого удаляют после предварительной сборки. При расчете в размерной цепи выбирают компенсирующее звено, назначают экономически достижимые допуски на все звенья размерной цепи и определяют допуск Т∑ и координаты середины поля допуска ∆○.
3. При методе компенсаторовточность замыкающего звена размерной цепи обеспечивают использованием спец. звеньев – компенсаторов. Эти звенья могут быть: а) неподвижными, б) подвижными.
В качестве подвижного используют прокладки, шайбы, втулки и т.д. Компенсирующее звено выполняется с такой же точностью, как и остальные составляющие звенья (рис.2.1.3).
Подвижные компенсаторы выполняются в виде устройства, которое позволяет бесступенчато регулировать размер компенсирующего звена в пределах величины компенсации. Здесь м.б. использованы планки, винты, клиновые устройства и т.д. Эти устройства широко используются в крупносерийном и массовом производстве (рис.2.1.4).
5 методов:
1)Полная взаимозаменяемость (брака нет, обеспечивается расчетом на max-min)
2)Неполная взаимозаменяемость: а) при вероятностном способе расчета
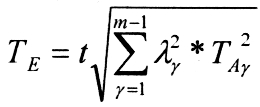
где t - коэффициент риска, А - показывает каков закон распределения размеров составляющего звена в пределах допуска, это коэффициент
относительного рассеивания. 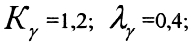
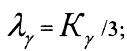
3) Групповой взаимозаменяемости (селективная сборка). Это сборка, при которой попарно работающие детали сортируют на группы по сопрягаемым размерам и соответствующим образом подбирают при сборке.
4)Регулирование -требуемая точность взаимного расположения звеньев.составляющих размерную цепь, достигается изменением действительных
размеров исходного, замыкающего или какого -либо другого звена. При этом изготовление деталей, образующих размерную цепь, упрощается и удешевляется, а точность сборочных единиц остается в заданных пределах.
5) Пригонка - когда на одно из звеньев остается припуск, который снимается во время или после сборки. Величина оставшегося припуска является величиной компенсации и определяется:
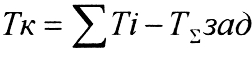
3.2. Расчет сборочных размерных цепей методом максимума-минимума. Основные расчетные зависимости. Прямая и обратная задачи расчета размерных цепей.
Размерной цепью называется замкнутая цепь размеров (звеньев размерной цепи), связывающих ряд поверхностей деталей в машине или механизме. Размерные цепи, определяющие взаимное расположение поверхностей, принадлежащих разным деталям в машине, и требующих ограничения погрешности их взаимного расположения при конструировании машин или их сборке, называют сборочными РЦ.
При решении размерных цепей может возникнуть два вида задач:
1.Определить необходимые параметры составляющих звеньев, обеспечивающих заданные значения замыкающего звена.
2.По известным параметрам составляющих звеньев определить номинальное значение и пределы изменения замыкающего звена.
Первую задачу, необходимость решения которой возникает при конструировании машин и проектировании технологии, называют проектной (прямой). Задача (обратная), как правило, проверочная.
При решении размерной цепи методом «максимум-минимум» используют две основные формулы:
(1) Т∑=∑│ξi│Тi, где i=1…n, Т∑ - предельное изменение размера замыкающего звена, Тi – допуск размера i-го звена, ξi – передаточное отношение i-го составляющего звена, n – число составляющих звеньев РЦ. Эта формула выражает соотношение м/у допусками составляющих звеньев и пределами изменения размера замыкающего звена. Вторая формула выражает положение верхнего и нижнего отклонения замыкающего звена относительно номинального размера:
2) ∆○∑= ∑ ξi*∆○i, где i=1…n, ∆○i – координата середины поля допуска i-го звена, ∆○∑ - координата середины поля рассеивания значений замыкающего звена.
Вместо этой формулы можно использовать следующие формулы:
ВО∑=∑ВОр-∑НОs;
НО∑=∑НОр-∑ВОs.
Р – увеличивающие звенья, s – уменьшающие звенья.
Для проектной задачи, когда заданы параметры лишь одного исходного звена РЦ, а число неизвестных параметров велико, существует много вариантов решений: метод подбора, метод равных допусков, метод единого квалитета.
При решении задачи первым методом подбирают такие параметры составляющих звеньев, чтобы при расчете на «max-min» удовлетворялись условия (1) и (2).
Сущность метода равных допусков заключается в том, что на все составляющие звенья назначают равные допуски Тi=Т. Тогда для метода расчета на «max-min» Т=Т∑/n.
Если среди составляющих звеньев есть звенья с уже назначенными допусками (например, подшипник качения), то из допуска замыкающего звена исключают сумму допусков звеньев с назначенными ранее допусками:
Т=(Т∑-∑Тст.i)/(n-nст.),
где i=1…nст., nст. – число звеньев с назначенными допусками. Иногда назначают на составляющие звенья одинаковые по величине допуски с одинаковым расположением относительно номинального размера (∆○i=∆○). ∆○=∆○∑/(np-ns).
Для вероятностного метода расчета соответствуют след. формулы:
где t – нормированный параметр распределения, λi – коэффициент относительного рассеяния i-го звена. В случае наличия в РЦ звеньев с ранее назначенными допусками:
Одинаковые отклонения для составляющих звеньев при условии αi=α м.б. определены по след. формуле: ∆○=∑∆○∑/(np-ns)–α*Т/2, где α – коэффициент относительного смещения составляющего звена.
Метод единого квалитета точностиобеспечивает одинаковую точность для любого звена. При расчете на «max-min» при назначении стандартных допусков равенство левой и правой части уравнения (1) нарушается, то допуск одного из составляющих звеньев необходимо ужесточить или расширить по сравнению с точностью остальных звеньев. Данное звено называют регулирующим Трег=Т∑-∑Тi, где i=1…(n-1). Для вероятностного метода расчета:
Отклонение всех звеньев, кроме регулирующего, назначают в соответствии со стандартными полями допусков по ГОСТ. Координату середины поля допуска регулирующего звена определяют по формуле:
∆○рег.=±(∆○∑-∑∆○р+∑∆○s),
где р=1…np, s=1…ns. «+» – если регулирующее звено регулирующее, «-« – если регулирующее звено уменьшающее.
Расчет размерных цепей
Расчет размерных цепей – нахождение неизвестных параметров звеньев размерной цепи.
С помощью теории размерных цепей решают две основные задачи:
Прямая задача – в большинстве случаев решается при конструировании.
Проектный расчет – известны параметры замыкающего звена, необходимо найти параметры составляющих звеньев.
Обратная задача – преимущественно решается при разработке технологических процессов изготовления и сборки изделий.
Поверочный расчет – известны параметры составляющих звеньев, необходимо найти параметры замыкающего звена.
Размерные цепи решаются методом, обеспечивающими полную и неполную взаимозаменяемость.
Расчет размерных цепей методом max-min, обеспечивающим полную взаимозаменяемость.
В дальнейшем используемые обозначения:
Aj (j = 1, 2, …, m-1) – номинальный размер произвольного звена размерной цепи.
А0 – номинальный размер замыкающего звена размерной цепи.
TAj, TA0 – допуски описанных выше размеров.
Ajmax, Ajmin, Ajc – предельные и среднии размеры звеньев цепи.
ES(Aj), EJ(Aj), Ec(Aj) – предельные и среднее отклонение размеров размерной цепи.
m – полное число звеньев размерной цепи.
n – число увеличивающих звеньев.
p – число уменьшающих звеньев.
n + p = m – 1 – замыкающее звено.
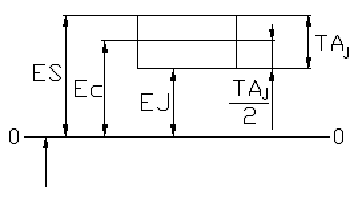
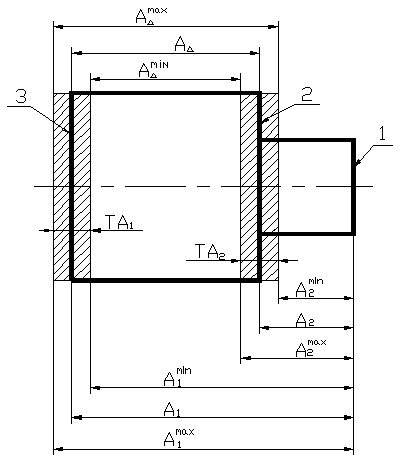
Сначала обрабатывают базовую плоскость 1, затем по настройке от этой базы – плоскость 2 по размеру A2 и плоскость 3 по размеру A1.
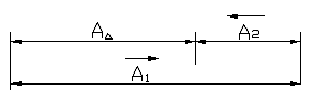
Поверочный расчет
Решение задач производится по формулам:

 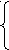

 ; ; 



Самым грубым размером в размерной цепи является замыкающий размер (т.к. его допуск равен сумме допусков составляющих звеньев). Поэтому, если к какому-либо размеру предъявляются высокие требования по точности, то нужно составить такую последовательность обработки, чтобы этот размер не был замыкающим, а был составляющим.
2. При конструировании необходимо соблюдать правило наикратчайшей размерной цепи, т.е. число звеньев в размерной цепи должно быть минимальным.
Проектный расчет
Заключается в распределении допуска замыкающего размера между составляющими.
В рамках метода max-min этот расчет осуществляется двумя способами.
Способ равных допусков.
Применяется, когда составляющие размеры близки по величине или принадлежат одному интервалу диаметров в таблице допусков.



Способ допусков одного квалитета (равноточных допусков).
Все составляющие звенья изготавливают по одному квалитету точности. Требуемый квалитет определяется следующим образом.
Допуск составляющего размера


D – среднегеометрический размер для интервала

по условию



T – в мкм. D – в мм.
По арасч определяем квалитет (арасч
aтабл).
По этому квалитету назначаем допуски на составляющие размеры
 , ,  , , 
Необходимо скорректировать допуски на составляющие размеры так, чтобы сумма Taj была равна TA0 (т.к.  , то , то  ). Скорректировать это значит уменьшить или увеличить допуск одного или двух составляющих размеров чтобы ). Скорректировать это значит уменьшить или увеличить допуск одного или двух составляющих размеров чтобы  . .
Назначаем предельные отклонения на составляющие размеры. Предельные отклонения на все составляющие размеры, кроме одного, назначаем как на основную деталь в системе образования посадок, т.е. на охватывающие размеры по «Н» (+), на охватываемые размеры по «h» (-), в трудноопределяемых случаях допуск назначается симметрично ( ). ).
Предельное отклонение одного размера определяется по формулам:


3.3. Расчет сборочных размерных цепей вероятностным методом. Основные расчетные зависимости.
Размерной цепью называется замкнутая цепь размеров (звеньев размерной цепи), связывающих ряд поверхностей деталей в машине или механизме. Размерные цепи, определяющие взаимное расположение поверхностей, принадлежащих разным деталям в машине, и требующих ограничения погрешности их взаимного расположения при конструировании машин или их сборке, называют сборочными РЦ.
Вероятностный расчет позволяет расширить допуски при изготовлении деталей с определенной вероятностью риска выхода параметров исходного звена за допустимые пределы, что при сборке м.б. исправлено повторной сборкой изделия.
При вероятностном способе расчета формула определения поля рассеивания значений замыкающего звена имеет вид: (1)
Расчет размерных цепей теоретически вероятностным методом основан на теории вероятностей.
В условиях единичного и массового производства при оптимально настроенном оборудовании размеры изготавливаемых деталей (рассеяние их размеров) подчиняются закону нормального распределения.
Отклонение размеров в основном группируются около середины поля допуска, а вероятность изготовления размеров деталей с предельными (верхним  и нижним и нижним  ) отклонениями весьма мала. ) отклонениями весьма мала.
Замыкающее звено размерной цепи принимаем за случайную величину, являющуюся суммой независимых случайных переменных, т.е. суммой независимых составляющих звеньев цепи.
 ……………(1) ……………(1)
Предположим, что границы вероятностного распределения составляющих и замыкающего звеньев совпадают с границами допусков, то при вероятности 0,27% риска можно принять
 или или  , ,
соответственно  ( При этом у 0,27% деталей размеры замыкающего звена будут выходить за пределы поля допуска). ( При этом у 0,27% деталей размеры замыкающего звена будут выходить за пределы поля допуска).
Подставляя  и и  в уравнение (1) получаем в уравнение (1) получаем
 ……………(2) ……………(2)
При других законах распределения (равной вероятности, закона треугольника) вводятся коэффициенты.

k0, kj – коэффициенты характеризующие отличие распределения погрешностей у составляющих и замыкающего звеньев от распределения по закону Гаусса.
При вероятностном расчете отклонения ES(A0) и EJ(A0) замыкающего звена определяют по формулам


Решение прямой задачи (проектный расчет) теоретико-вероятностным методом. Эта задача решается аналогично методике, изображенной для прямой задачи по методу max-min.
Способ равных допусков


Способ допусков одного квалитета

Применение теоретико-вероятностного метода расчета расчетных цепей по сравнению с методом max-min позволяет:
При решении обратной задачи, по известным допускам составляющих определить более узкий допуск замыкающего звена.
При решении прямой задачи, по заданному допуску замыкающего звена назначить более грубые, т.е. технологически выполняемые допуски составляющих звеньев.
Например:
n=4; TA0=8мкм


Метод групповой взаимозаменяемости
Селективная сборка
Сущность – изготовление деталей со сравнительно широкими технологическими, выполнимыми допусками, сортировке деталей на равное число групп с более узкими групповыми допусками и сборке их (после комплектовании) по одноименным группам.
Применяют когда средняя точность размеров цепи очень высокая и экономически неприемлема.
Преимущества:
Позволяет обрабатывать детали с более широкими допусками, при обеспечении необходимой точности. (в n раз повышается точность сборки без уменьшения TD на изготовления).
Недостатки:
Усложняется контроль (требуется большой штат контролеров, измерительно-сортировочное оборудование), повышается трудоемкость сборки, увеличение незавершенного производства, т.к. разное число деталей в группах.
Применяется в массовом и крупносерийном производстве, когда затраты на сортировку, сборку окупаются высоким качеством. При производстве подшипников качения и сборке ответственных резьбовых соединений селективная сборка единственная экономически целесообразная.
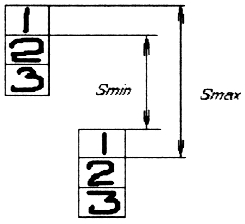
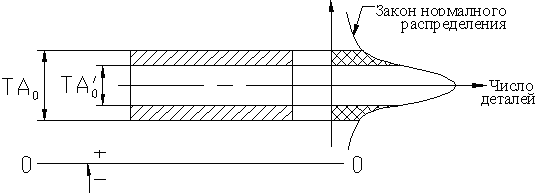
При селективной сборке Nmax и Smin уменьшают, а Smax и Nmin увеличивают, прибли-жаясь с увеличением числа групп сортировки к Nm и Sm для данной посадки, что делает соединения более долго-вечными.
Для установления числа групп n сортировки деталей необходимо знать тре-буемые предельные значения групповых SN, которые находятся из условия обеспечения долговечности соединения, либо допускаемое значение группового допуска, определяемого экономической точностью сборки и сортировки. TD=Td
Групповой N и S остаются постоянными при переходе от одной группы к другой.
При сборке деталей для повышения долговечности подвижных соединений необходимо создавать наименьший допускаемый зазор, для повышения работоспособности соединений с натягом – наибольший допускаемый натяг.
Число n подсчитывается по следующим формулам (для подвижных посадок):

При заданном 


При TD>Td групповой S, N при переходе от одной группы к другой не остается постоянным, следовательно, однородность соединений не обеспечивается, поэтому селекционную сборку целесообразно применять при TD=Td.
При большом числе групп сортировки групповой допуск незначительно отличается от допуска групп при меньшем числе групп, но при этом усложняется организующий контроль и сложность сборки значительно возрастает.

Лишь в подшипниковой промышленности при сортировке тел качения  . .
|
|
|
 Скачать 28.29 Mb.
Скачать 28.29 Mb.