1. Технологический процесс и его структура Технологическим процессом

• Название: 1. Технологический процесс и его структура Технологическим процессом
• Анкор: Otvety_na_voprosy.doc
• Дата: 03.03.2018
• Размер: 28.29 Mb.
• Имя файла: Otvety_na_voprosy.doc
• Тип: Документы; #16160
• страница: 5 из 20

Нормирование параметров шероховатости поверхности

Выбор параметров шероховатости поверхности производится в соответствии с ее функциональным назначением.

Основным во всех случаях является нормирование высотных параметров. Предпочтительно, в том числе и для самых грубых поверхностей, нормировать параметр Я_а, который лучше отражает отклонения профиля, поскольку определяется по значительно большему числу точек, чем R_z.

Параметр R_zнормируется в тех случаях, когда прямой контроль П_а с помощью профилометров невозможен (режущие кромки инструментов и т. п.).

Числовые значения параметров Я_а и R_zприведены в приложении 3. Следует применять в пер­вую очередь предпочтительные значения.

В настоящее время существует несколько способов назначения шероховатости поверхности.

1. Имеются рекомендации [10] по выбору числовых значений для наиболее характерных видов сопряжений, часть которых приведена в табл. 3.12.

Таблица 3.12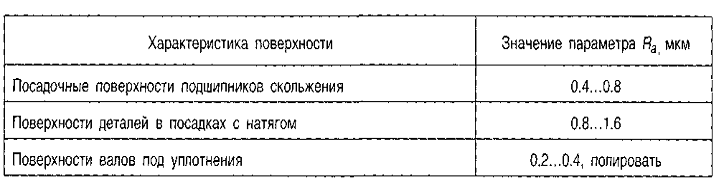

2. 
   Шероховатость устанавливается стандартами на детали и изделия, а также на поверхности, с которыми они сопрягаются, например требования к шероховатости поверхностей под подшипники качения (табл. 3.13).
   
3. 
   Когда отсутствуют рекомендации по назначению шероховатости поверхности, ограничения шероховатости могут быть связаны с допуском размера (IT), формы (TF) или расположения (ТР).
   

Большинство геометрических отклонений детали

Таблица 3.13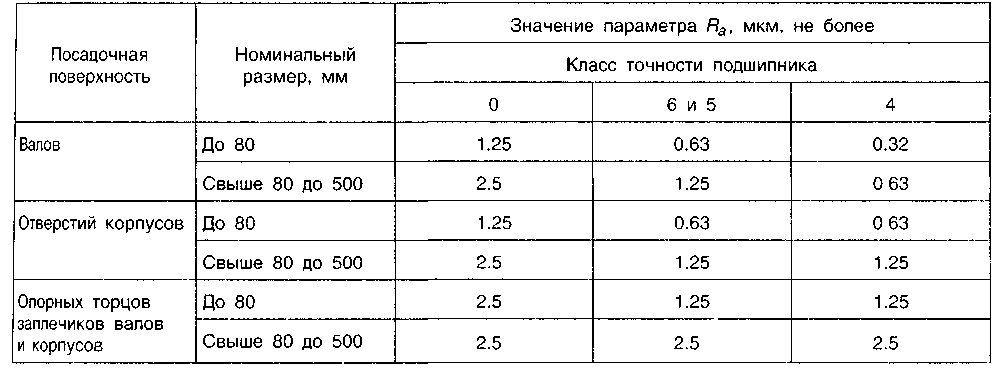



должно находиться в пределах поля допуска размера (рис. 3.14).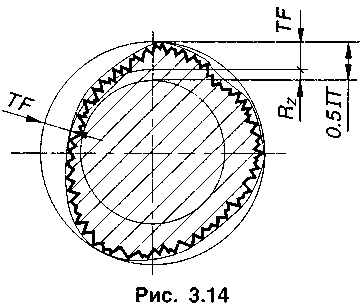



Поэтому величину параметра R_zрекомендуется назначать не более 0.33 от величины поля допуска на размер либо 0.5...0.4 от допуска расположения или формы. Если элемент детали имеет все три допуска, то следует брать допуск с наименьшей величиной.

Переход от параметра R_zк параметру R_aпроизводится по соотношениям [7]:



После определения параметр Я_а округляют до ближайшего числа из ряда стандартных значений (см. приложение 3).

Пример 1

На чертеже детали задан размер Определить параметр шероховатости

Решение

Допуск размерамкм. Параметрмкм. Параметр= 0.2-5.3 = 1.06 мкм. Для нанесения на чертеже детали принимаем= 0.8 мкм.

Пример 2

На чертеже детали заданы , допуск радиального биения ТР = 9 мкм и отклонение от цилиндричностимкм. Определить параметр шероховатости

Решение

Допуск размера 17= 13 мкм, допускмкм, поэтому параметр мкм. Параметр R_a= 0.2 R_z= 0.2 • 2 = 0.4 мкм. Для нанесения на чертеже детали принимаем R_a= 0.4 мкм.
Обозначение шероховатости поверхностей

Шероховатость поверхности обозначают на чертеже для всех выполняемых по данному черт(поверхностей изделия, независимо от методов их образования, кроме поверхностей, шерохотость которых не обусловлена требованиями конструкции.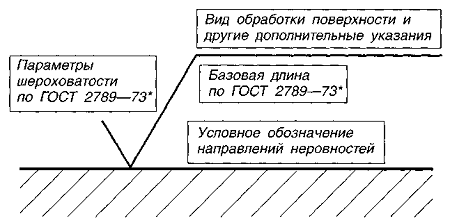



Для обозначения на чертежах шероховатости поверхности применяют знаки, приведенные рис. 3.16.

Числовые значения параметров шероховатости указываются после соответствующего симво, (R_Z20, R_maK10), кроме значений параметра П_а, который проставляется без символа (рис 3.16)







Обозначения шероховатости поверхности, в которых знак не имеет полки, располагают относительно основной надписи чертежа так, как показано на рис. 3.17.

При указании одинаковой шероховатости для части поверхностей изделия в правом верхнем углу чертежа помещают обозначение одинаковой шероховатости и знак шероховатости в скобках.

Знак в скобках означает, что все поверхности, на которых на изображении не нанесены обозначения шероховатости, должны иметь шероховатость, указанную перед скобками.

П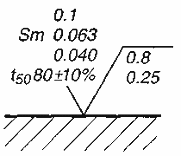ример указания шероховатости поверхности приведен на рис. 3.19.
При указании двух и более параметров шероховатости поверхности в обозначении шероховатости значения параметров записывают сверху вниз в следующем порядке:

• 
  параметр высоты неровностей профиля;
  
• 
  параметр шага неровностей профиля;
  
• 
  относительная опорная длина профиля.
  

В обозначении указано (рис. 3.19):

1. 
   Среднее арифметическое отклонение профиляне более 0.1 мкм на базовой длине I = 0.25 мм (в обозначении длина не указана, так как соответствует значению, определенному стандартом для данной высоты неровностей).
   
2. 
   Средний шаг неровностей профилядолжен находиться в пределах от 0.063 мм до 0.04 мм на базовой длине / = 0.8 мм.
   
3. 
   Относительная опорная длина профиля на 50% уровне сечения должна находиться в пределах 80 ± 10% на базовой длине I= 0.25 мм.
   

1.14. Анализ точности методом кривых распределения

Основой метода является построение кривых распределения случайных значений геометрических размеров.

Методика построения эмпирической кривой распределения

Рассмотрим эту методику. Пусть имеется партия из п деталей. Величину п будем называть объемом выборки. Допустим размеры деталей в этой партии являются случайными величинами. Эмпирическая кривая распределения отражает закон размеров в пределах поля их рассеяния. Эта кривая строится в следующей последовательности: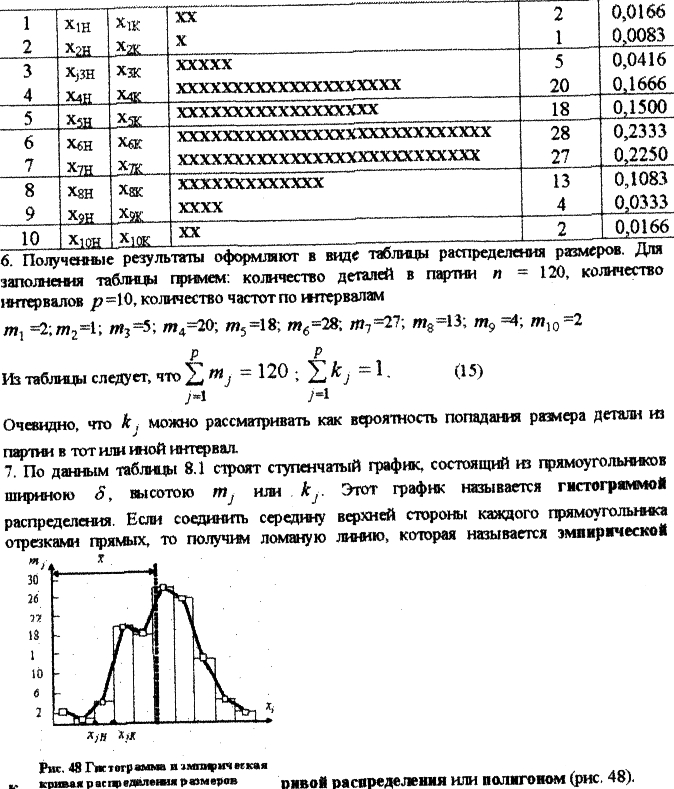





Графическая интерпретация полученных результатов позволяет сделать вывод, что размеры группируются около некоторой центральной величины (центра группирования), причем, чем больше отличие между этой величиной и фактическим размером, тем меньше частота регистрации этого размера. Эта центральная величина называется средним арифметическим значением случайной величины и определяется по следующей формуле

Очевидно, что х_}- - значение размера в середине j - го интервала. Другой характеристикой кривой распределения случайных величин, является среднее квадратическое отклонение случайной величины от среднего арифметического значения, которое определяется по формуле

Если постепенно увеличивать размер партии, то ломаная линия будет приближаться к холмообразной кривой, аналогичной той, которая представлена на рис.49. Тогда частота m_j и частность k_jна каждом интервале будут стремиться к своим теоретическим значениям m'jи k'jна данном интервале.

8.3.1.2. Закон нормального распределения и его свойства

В математической статистике теоретическая частность определяется следующим выражением называется плотностью распределения случайной величины. Функция, представленная этим выражением, отражаем законом нормального распределения. График этой функции представлен на рис.49 и называется кривой нормального распределения.

Из формулы (18) следует, что плотность распределения случайной величины для линейных размеров имеет размерность обратную длине, т.к. среднее квадратическое отклонение имеет данную размерность. Плотность распределения следует рассматривать, как величину, показывающую насколько велика вероятность появления случайной величины в окрестности некоторой точки на отрезке единичной длины. В окрестностях х_n = х плотность распределения максимальная, т.е. вероятность появления случайной величины в окрестностях этой точки максимальная. С увеличением разности х - х плотность распределения уменьшается.

Чтобы лучше усвоить понятие плотности распределения, можно провести аналогию с плотностью вещества, которая определяется как масса, содержа­щаяся в единице объема. Представим себе стержень, плотность вещества которого меняется по длине согласно некоторому закону. Тогда, чтобы определить массу участка стержня, необходимо вычислить определенный интеграл от плотности его материала в пределах этого участка. Следуя этой аналогии, чтобы определить вероятность появления случайной величины х в некотором интервале х₁ <=х<=х₂, плотность распределения которой подчиняется нормаль­ному закону, необходимо вычислить интеграл



Геометрически I(x) представляет собой площадь фигуры на отрезке [х₁, х₂ ] под кривой нормального распределения. Для достаточно узкого интервала согласно теореме о среднем

Кривая нормального распределения

1. Ось х является асимптотой для ее ветвей.

2. При х = х;

(17,а)

(18)

(19)

(20)

3. Кривая имеет две точки перегиба А и В, которые находятся на расстоянии от оси симметрии. Ординаты их равны

4. Если случайная величина следует нормальному закону распределения и может принимать любые численные значения в интервале - < х < + , то

5. Положение кривой относительно начала координат, и ее форма определяются двумя параметрами и . С изменением при постоянном форма кривой остается прежней. Изменяется ее положение относительно начала координат (рис. 50). С изменением сигма центр кривой остается на прежнем месте. Изменяется ее форма (рис.51).

Докажем справедливость равенства (23). Если это условие выполняется, то для любого другого интервала, х^ х х₂

Введем новую переменную. Это действие называется нормированием. Графическая интерпретация процедуры нормирования заключается в совмещении начала новой системы координат (t, у) с центром группирования. В этом случае кривая нормального распределения становится симметричной относительно оси у. После замены переменной в (24) получаем

где и - новые пределы интегрирования. Допустим /, = -t; t-) - +t . Теперь где называется функцией Лапласа, значение которой задано в таблицах.

(22)

(21)

(23)

(24)

(25)

(26)

Интеграл (26) нельзя выразить в элементарных функциях. Его можно вычислить, если представить подынтегральную функцию в виде в виде бесконечного степенного ряда с последующим его интегрированием. В результате будем иметь:

Из выражения (27) следует, что при , . Таким образом, равенство

(23) доказано. Так как интегралами (23) - (26) определяется вероятность появления случайной величины в заданном интервале ее изменения.

Геометрически указанные интегралы представляют собой площадь под кривой нор­мального распределения в пределах заданного интервала. Поэтому согласно (23) независимо от значений и эта площадь, при изменении случайной ве­личины в пределах - < х < + , всегда одинакова и равна единице. Для меньшего интервала она меньше единицы.

С помощью функции Лапласа можно определить теоретические частность и частоту. Из выражений (17,а) и (18) получаем

(28)

(27)

Пусть , а . В результате нормирования (заме-

ны переменной) будем иметь

Или при достаточно малом отрезке приближенно получаем

(30)

1.15. Анализ точности методом точечных диаграмм

Анализ точности методом кривых распределения позволяет сделать заключение о точности законченного этапа технологического процесса и дать про­гноз для следующего этапа. При этом заключение о точности процесса делают на основании измерений сравнительно небольшой партии деталей - выборке.анализ учитывает влияние на точность случайных погрешностей.

При изготовлении деталей в течение длительного времени, когда партии деталей становятся большими, на точность изготовления влияют дополнительно систематические погрешности. Такие, например, как из-за износа инструмента и температурных деформации системы ДИПС. В этом случае центр группирования случайных величин постепенно смещается. Меняется также поле рассеяния. Таким образом, параметры кривой распределенияистановятся зависимыми от времени. Закон нормального распределения при этом нарушается.

Кроме того, оказывают влияние изменения в настройке режущего инстру­мента, а также его смена. В результате этих действий происходит резкое смещение центра группирования случайных величин, как это показано на рис. 50, а также резкое изменение поля рассеяния. Параметры кривой распределения ипосле этих действий меняются. Поэтому кривая нормального распределе­ния становится другой. В частности, если смена инструмента была осуществлена во время изготовления партии деталей, которая затем была использована как выборка при статистической обработке, то кривая распределения может иметь две вершины (рис. 55). Таким образом, при анализе точности методов кривых распределения отсутствует фактор времени. Это является недостатком данного метода.

Метод точечных диаграмм не имеет этого недостатка.

т.к. анализ точности ведется постоянно на протяжении изготовления всей партии деталей и не только выборки из нее.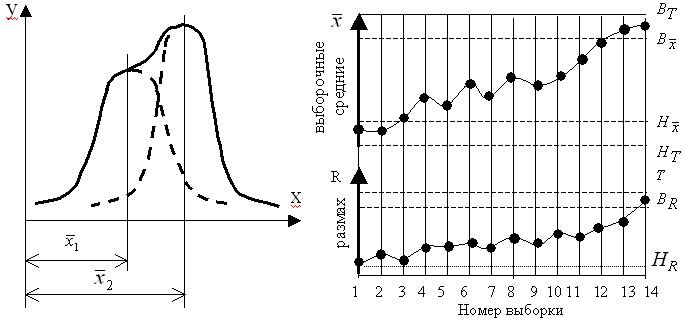