ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 10 из 15

Системы уравнений четырехполюсника.Основной задачей теории четырехполюсников является установление соотношений между четырьмя величинами: напряжениями на входе и выходе, а также токами, протекающими через входные и выходные зажимы. Уравнения, дающие зависимость между U_1, U_2, I_1, I_2, называются уравнениями передачи четырехполюсника.Для линейных четырехполюсников эти уравнения будут линейными. Величины, связывающие в уравнениях передачи напряжения и токи, называются параметрами четырехполюсников.

Сложная электрическая цепь (например, канал связи), имеющая входные и выходные зажимы, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Зная параметры этих четырехполюсников, можно вычислить параметры сложного четырехполюсника и получить тем самым зависимость между напряжениями и токами на зажимах результирующего сложного четырехполюсника, не производя расчетов всех напряжений и токов внутри заданной схемы.

Кроме того, теория четырехполюсников позволяет решить обратную задачу: по заданным напряжениям и токам найти параметры четырехполюсника и затем построить его схему и рассчитать элементы, т. е. решить задачу синтеза.

Пусть четырехполюсник содержит пнезависимых контуров. Отнесем первый контур ко входу четырехполюсника (I_K1 =I₁), второй контур — к его выходу (I_K2 = I_K2). Будем считать, что во внутренних контурах четырехполюсника отсутствуют независимые источники энергии.

При рассмотрении четырехполюсника важно заранее условиться о положительных направлениях напряжений и токов. В дальнейшем будем придерживаться положительных направлений, показанных стрелками на рис. 12.1, если особо не будут оговорены другие случаи.

Составим систему уравнений для контурных токов (см. § 2.4):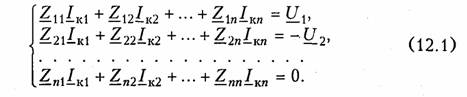





Коэффициенты Y₁₁, Y₁₂,Y₂₁, и Y₂₂, в уравнениях (12.2) называются Y-.параметрами, или параметрами проводимостейчетырехполюсника, так как по размерности они являются именно таковыми. Уравнения (12.2) называются уравнениями передачи четырехполюсника в Y-параметрах. Эти уравнения представляют собой одну из возможных форм уравнений передачи. Она позволяют находить любую пару из значений I₁,I_2,U_1, и U_2,, если заданы значения другой пары.

Помимо уравнений в форме (12.2) существует еще пять форм уравнений передачи. Уравнения, связывающие напряжения U_1, U_2,  и токи I₁, I₂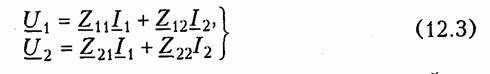



содержат в качестве коэффициентов параметры сопротивленийчетырехполюсника, или Z-параметры, и называются уравнениями передачи в Z-параметрах. Параметры Z₁₁, Z₁₂, Z₂₁ и Z₂₂ имеют размерность сопротивлений. Заметим, что они не являются обратными величинами по отношению к параметрам проводимости, таким образом, например,  Не следует также путать эти параметры с собственными и взаимными сопротивлениями контуров Z₁₁, Z₁₂ и т. д. в уравнениях (12.1) для контурных токов.

Коэффициенты, входящие в систему уравнений, связывающую входные U_1, и I₁ и выходные U_2,  и I₁ напряжения и токи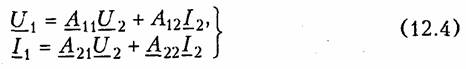



называются   А-параметрами,  или   обобщенными   параметрами.Уравнения (12.4) называются уравнениями передачи в А- параметpax. Параметры А₁₁и А₂₂являются безразмерными, параметр А₂₁имеет  размерность  сопротивления;   параметр А%\   — размерность проводимости:

     Приведем еще две формы уравнений передачи: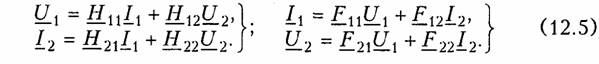



Коэффициенты Н₁₁,Н₁₂,Н₂₁и Н₂₂называются H-параметрамии применяются при рассмотрении схем с транзисторами. Параметры Н₁₂ и Н₂₁являются безразмерными, а параметры Н₁₁ и Н₂₂имеют размерности сопротивления и проводимости.

Коэффициенты F₁₁, F₁₂, F₂₁ и F₂₂называются F-параметрамии применяются при рассмотрении схем с электронными лампами. Параметры F₁₂ и F₂₁ безразмерные, а параметры F₁₁иF₂₂ имеют размерности проводимости и сопротивления. Уравнения (12.5) называются соответственно уравнениями передачи в H-параметрахи F-параметрах.

Все формы уравнений передачи принципиально равноправны. Выбор той или иной формы зависит исключительно от задачи, которая в данном случае решается.

Полная совокупность параметров любой системы уравнений передачи образует систему параметров четырехполюсника. Так, систему Y-параметров четырехполюсника образует совокупность его параметров Y₁₁, Y₁₂,Y₂₁, Y_22.

Два четырехполюсника, имеющие одинаковые системы параметров, независимо от их внутренней структуры, числа элементов и т. д., характеризуются, очевидно, одинаковыми уравнениями передачи. Такие четырехполюсники называются эквивалентными,и при включении любого из них между одними и теми же внешними цепями на их зажимах устанавливаются одинаковые режимы.

Свойства параметров-коэффициентов.Системы Y-,Z-, А-, Н-иF-параметров образованы из коэффициентов уравнений передачи, и поэтому часто их объединяют одним названиемпараметры-коэффициенты.Рассмотрим основные свойства параметров-коэффициентов.

1. Параметры-коэффициенты определяются только схемой четырехполюсника и ее элементами и не зависят от внешних цепей, между которыми может быть включен четырехполюсник, т. е. они характеризуют собственно четырехполюсник.

Пример.На входе Г-образного четырехполюсника (см. рис. 12.2, б), подключенного к внешним цепям, действует напряжение U₁и ток I₁,а на выходе напряжение U₂и ток I₂.ОпределимА-параметры четырехполюсника.

В соответствии с ЗНК и ЗТК U₁ = U₂+I₁Z₁иI₁=U₂/Z₂+I_2.

Подставляя выражение для тока I₁в первое равенство, получаем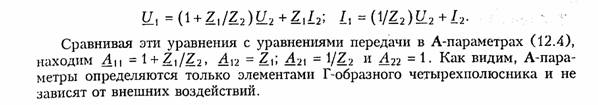



2. Все системы параметров-коэффициентов описывают один и тот же четырехполюсник, поэтому между различными системами параметров-коэффициентов существует однозначная взаимосвязь.

Пример.Установим связь между А-параметрами и Z-параметрами. Решая систему уравнений в Z-параметрах (12.3) относительно неизвестных U₁и I₁находим: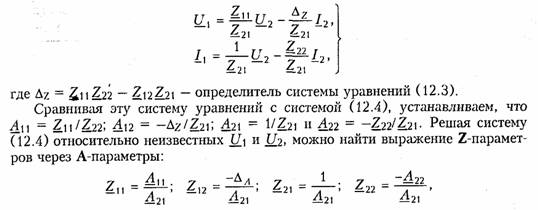



Аналогичным образом можно установить связь между другими системами параметров. В табл. 12.1 приведены соотношения между различными системами параметров — коэффициентов.

3. Пассивный четырехполюсник полностью характеризуется не более чем тремя независимыми параметрами. Действительно, в многоконтурной схеме пассивного четырехполюсника взаимные сопротивления Z_kmи Z_kmk-гои т-токонтуров равны между собой. Следовательно, Y₁₂= —Y₂₁ .Зная связь между Y-параметрами и Z-параметрами, можно установить, что Z₁₂ = —Z_21.. Далее можно показать, что для А-параметров справедливо соотношение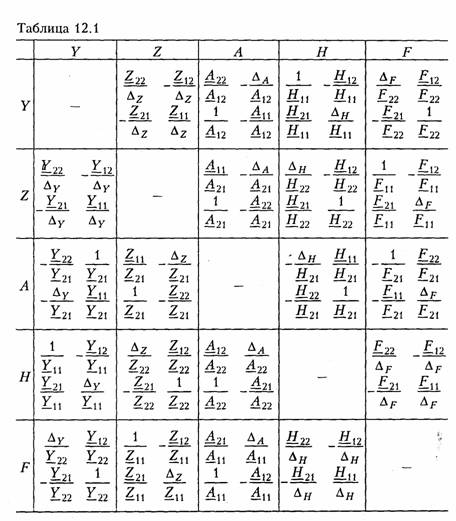





=Н_{21 ,}Н₂₂;F_11,F₁₂=F₂₁и F₂₂или любые три из параметров А₁₁,А_12,А₂₁иА_22.

4. При изменении направления передачи энергии через четырехполюсник во всех выражениях, включающих А-параметры, коэффициенты А₁₁ и А₂₂ меняются местами.

Рассмотрим передачу энергии через четырехполюсник в обратном направлении, т. е. от зажимов 2—2'к зажимам 1 —1' (рис. 12.3). Если в уравнениях передачи (12.4) заменить напряжение U₁и ток  I₁на зажимах 1— 1' на напряжение U₂`и I<sub>2</sub>`ток —в соответствии с рис. 12.3, анапряжение U₂и ток I₂на зажимах 2 — 2'на величины —U₁`и —I<sub>1</sub>`,то (12.4) можно переписать в виде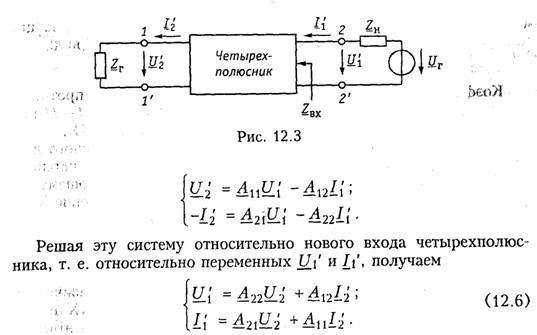



Сопоставляя эти уравнения с (12.4), можно сделать интересное наблюдение: в уравнениях передачи параметры А₁₁ и А₂₂ поменялись местами. Оказывается, этот факт справедлив не только для уравнений передачи, но и для любых других выражений, в которые входят А-параметры.

5. Симметричные пассивные четырехполюсники имеют только два независимых параметра. В самом деле, в случае симметричного пассивного четырехполюсника не имеет значения направление передачи энергии: напряжения и токи на входе и выходе не изменяются при замене местами зажимов. Сравнивая уравнения передачи (12.4) и (12.6), устанавливаем, что А₁₁ = А₂₂. Из табл. 12.1 находим также, что в симметричных четырехполюсниках Y₁₁ =-Y₂₂; Z₁₁= -Z₂₂ и Δ_Н = -1.



6. Параметры-коэффициенты имеют определенный физический смысл. Для выявления этого физического смысла следует четырехполюсник поставить в такой режим работы, при котором уравнения передачи содержат лишь один интересующий нас параметр. Подобное произойдет, если использовать режимы холостого хода (XX — размыкания пары зажимов) и короткого замыкания (КЗ — замыкания накоротко пары зажимов). Так, при XX на зажимах 2 — 2' (см. рис. 12.1) ток I₂=0. Тогда уравнения передачи, содержащие ток I₂,например уравнения (12.3) в Z-параметрах, имеют вид:



7. Из предыдущего свойства следует, что параметры-коэффициенты являются комплексными величинами, так как они определяются отношением комплексных амплитуд (действующих значений) напряжений и токов. В случае анализа четырехполюсника в режиме негармонических колебаний используют спектральные представления электрических величин. Можно показать, что параметры-коэффициенты, рассматриваемые относительно не отдельной частоты, а определенного спектра частот, являются рациональными функциями оператора jω. При переходе от оператора jω к оператору рпараметры-коэффициенты представляют собой рациональные функции оператора р.



т. е. Z₁₁является дробно-рациональной функцией оператора рс положительными вещественными коэффициентами. Нули этой функции  — мнимые и лежат на мнимой оси комплексной плоскости, полюс р₁=0. При замене оператора роператором jω переходим к частотной характеристике



Полученные выражения Z₁₁ (p) и Z₁₁ (jω) напоминают выражение входного сопротивления последовательного LС-контура. Это объясняется тем, что входное сопротивление Г-образной цепи (см. рис. 12.2, б)при разомкнутых зажимах определяется последовательным соединением двухполюсников Z₁, и Z₂ (индуктивности и емкости), т. е. Z₁₁является сопротивлением двухполюсника (ср. с (4.115)).

 

4.3. Применение матриц к расчету четырехполюсников

 

Уравнения передачи в матричной форме.Любую из систем уравнений передачи четырехполюсника можно записать в матричной форме. В частности, для системы уравнений в Y-параметрах (12.2)



Расчет соединений четырехполюсников.Сложные четырехполюсники можно представить в виде различных соединений простых четырехполюсников. При этом параметры сложного четырехполюсника могут быть найдены по параметрам образующих его простых четырехполюсников.

На рис. 12.4 показана схема каскадного соединениядвух четырехполюсников. В соответствии с обозначениями на рисунке при каскадном соединении Длякаждого из четырехполюсников можно составить матричные равенства:



Таким образом, матрица А результирующего четырехполюсника при каскадном соединении равна произведению одноименных матриц соединенных четырехполюсников: А = А'А". Это правило распространяется на любое число каскадно соединенных четырехполюсников, причем матрицы должны записываться впорядке следования четырехполюсников, так как умножение матриц не подчиняется переместительному закону.

При последовательном соединениидвух (или большего числа) четырехполюсников (рис. 12.5) удобно пользоваться матрицами Z. Для этого вида соединения 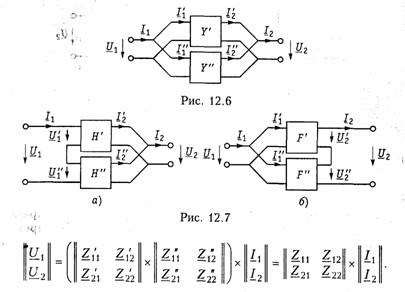т. е. напряжения на выходах и входах отдельных четырехполюсников в результирующем четырехполюснике складываются. Записывая уравнения передачи в Z-форме для каждого четырехполюсника





При последовательном соединении четырехполюсников матрица Z результирующего четырехполюсника равна сумме одноименных матриц соединенных четырехполюсников: Z=Z' +Z".

Совершенно аналогично доказывается, что при параллельном соединениичетырехполюсников (рис. 12.6), где  и матрица Y результирующего четырехполюсника равна сумме одноименных матриц соединяемых четырехполюсников: Y=Y' +Y".

Матрицы F удобно применять при смешанном — последовательно-параллельномсоединении четырехполюсников (рис. 12.7, а).При этом Н = Н' + Н".

Матрицы F удобно применять при параллельно-последовательномсоединении четырехполюсников (рис. 12.7, б). При этом F= F'+ F".