ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 2 из 15

Активные элементы. Активными элементами электрической цепи являются зависимые и независимые источники электрической энергии. К зависимым источникам относятся электронные лампы, транзисторы, операционные усилители и другие, к независимым источникам — аккумуляторы, электрогенераторы, термоэлементы, пьезодатчики и другие преобразователи. Независимые источники можно представить в виде двух моделей: источника напряжения и источника тока.

Независимым источником напряженияназывают идеализированный двухполюсный элемент, напряжение на зажимах которого не зависит от протекающего через него тока. Условное обозначение источника напряжения показано на рис. 1.5, а.

Источник напряжения полностью характеризуется своим задающим напряжением щ,или электродвижущей силой(ЭДС) е_Г(рис. 1.5, в).Внутреннее сопротивление источника напряжения равно нулю н иногда при изображении источника напряжения обозначают знаком «+>> только один из зажимов и не показывают стрелкой положительное направление е_Гимея в виду, что оно действует от «+» к «—» (рис. 1.5, б). Часто при анализе цепей ограничиваются изображением только зажимов источника напряжения, как показано на рис. 1.1, б.

Вольт-амперная характеристика идеального источника напряжения представляет собой прямую, параллельную оси токов (рис. 1.6. а).Такой идеализированный источник способен отдавать во внешнюю цепь бесконечно большую мощность. Ясно, что физически такой источник реализовать нельзя. Однако в определенных пределах изменения тока он достаточно близко отражает реальные свойства независимых источников.

Независимым источником токаназывают идеализированный двухполюсный элемент, ток которого не зависит от напряжения на его зажимах.  Условное обозначение источника тока показано на рис.  1.5,  г. Источник тока полностью характеризуется своим задающим током i_Г.Внутренняя проводимость источника тока равна нулю (внутреннее сопротивление бесконечно велико) и ВАХ представляет собой прямую, параллельную осп напряжений (рис. 1.6, б). Такой источник также способен отдавать во внешнюю цепь бесконечно большую мощность и является идеализацией реальных независимых источников.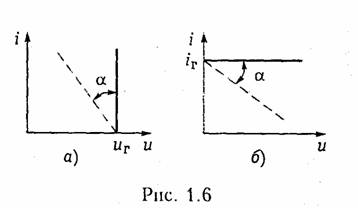



Свойства реальных источников с конечным внутренним сопротивлением R_Tможно моделировать с помощью независимых источников напряжения и тока с дополнительно включенными резистивными сопротивлениями R_Гили проводимостью G_Г (см. рис. 1.5, д, е).Напряжение ии отдаваемый ток iэтих источников зависят от параметров подключаемой к ним цепи, а их В АХ имеет тангенс угла наклона α, пропорциональный R_Ги G_Г соответственно (штриховые линии па рис. 1.6).

Однако свойства целого ряда электронных устройств нельзя описать моделью соединенных между собой указанных выше независимых источников и пассивных двухполюсных элементов. К числу таких устройств относятся электронные лампы, транзисторы, операционные усилители и другие электронные приборы. Это так называемые зависимые пли управляемые источники.

Зависимый источникпредставляет собой четырехполюспый элемент (рис. 1.7) с двумя парами зажимов — входных (/, /') н выходных (2, 2').Входные ток i₁и напряжение и₁являются управляющими. Различают следующие разновидности зависимых источников:     источник  напряжения,   управляемый  напряжением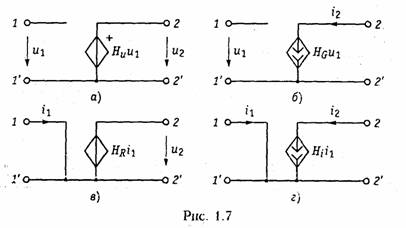

 



 

(ИНУН); источник тока, управляемый напряжением (ИТУН); источник напряжения, управляемый током (ИНУТ); источник тока управляемый током (ИТУТ). На рис. 1.7 показаны условные обозначения зависимых источников различного типа.

В ИНУН (рис. 1.7, а)входное сопротивление бесконечно велико, входной ток i₁= 0, а выходное напряжение и₂связано со входным и₁равенством и₂—H_uu₁,где Н и— коэффициент, характеризующий усиление по напряжению зависимого источника. Источник типа ИНУН является идеальным усилителем напряжения.

 ИТУН (см. рис. 1.7, б) выходной ток i₂ управляется входным напряжением u₁причем i₁= 0 и ток i₂ связан с и₁равенством где Н_G— коэффициент, имеющий размерность проводимости.

В ИНУТ (рис. 1.7, е) входным током i₁управляется выходное напряжение i₂,входная проводимость бесконечно велика: u₁=0, i₂ =H_Ii_2 1,где Hi— коэффициент, имеющий размерность сопротивления.

В ИТУТ (рис. 1.7, г) управляющим током является i₁,а управляемым i₂. Входная проводимость ИТУТ, как и ИНУТ, бесконечно велика, где Hi—коэффициент, характеризующий усиление по току. Источник типа ИТУТ является идеальным усилителем тока. Коэффициенты Н_uН_G,HR,Hi,представляют собой вещественные положительные или отрицательные числа и полностью характеризуют соответствующий источник.

Примером зависимого источника является операционный усилитель (ОУ). Выпускаемые в виде отдельной микросхемы (рис. 1.8, а)ОУ широко применяются в качестве активных элементов электрической цепи.

Операционный усилитель имеет два входа: 1 — неинвертирующий и 2 —инвертирующий. При подаче напряжения и₁на вход 1 — выходное напряжение u₂ имеет ту же полярность, что и u₂а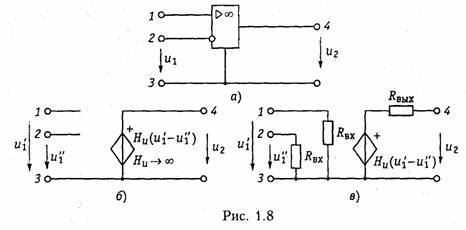

 



при подаче u₂на вход 2напряжение u₂меняет свою полярность па противоположную.

Идеальный ОУ (рис. 1.8, б) представляет собой ИНУН с бесконечно большим коэффициентом усиления (Ни→∞), бесконечно большими входным сопротивлением и выходной проводимостью (выходное сопротивление равно нулю).

Реальный ОУ можно представить в виде ИНУНа с конечными входным R_BXи выходным R_выхсопротивлениями (рис. 1.8, в).

Кроме ОУ в качестве активных элементов электрических цепей широко используются различные электронные и полупроводниковые приборы: электронные лампы, биполярные и полевые транзисторы и др.

На рис. 1.9, априведена электронная лампа (триод) и ее модели (эквивалентные схемы замещения)в форме ИТУН (рис. 1.9, б) и ИНУН (рис. 1.9, в), где обозначены Gi = 1/Ri, — внутренняя проводимость лампы, S= di₂/du—крутизна; μ = SRi,— коэффициент усиления лампы. Параметры Gi, S, μ обычно приводятся в справочниках. Эти эквивалентные схемы являются линейными и могут использоваться в области низких частот. В нелинейном режиме работы активного элемента используются более сложные модели (см. гл. 10, 11). В области высоких частот в моделях активных элементов появляются кроме резисторов, реактивные элементы — обычно емкость (см. табл. 1.1).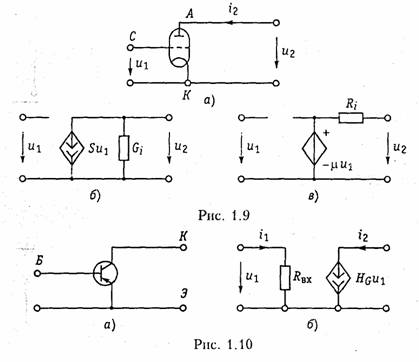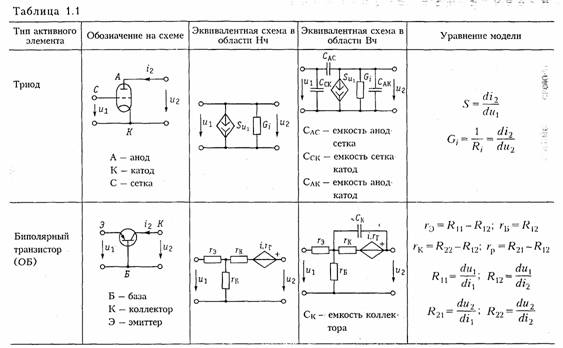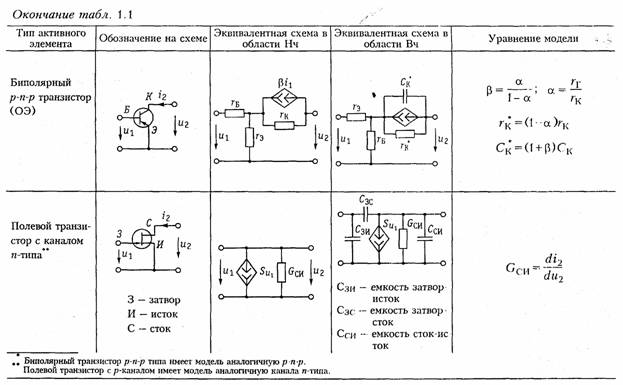

 



 



 



 

Транзисторы, как правило, имеют более сложную структуру, чем лампы и описываются в зависимости от решаемых задач более сложными моделями [2].Наиболее распространенными для биполярных транзисторов являются образные и /7-образные эквивалентные схемы замещения, причем, последние можно получить из первых методами преобразования «звезда — треугольник» (см. § 1.5). В табл. 1.1 приведены образные схемы замещения биполярных транзисторов, включенных по схеме с общей базой (ОБ) и общим эмиттером (ОЭ) в области низких и высоких частот и основные соотношения, описывающие их модели.

Иногда для анализа цепей с биполярными транзисторами используются модель ИТУН с конечным входным сопротивлением (рис. 1.10). Для полевых транзисторов обычно используется модель в форме ИТУН (табл. 1.1).

Кроме рассмотренных эквивалентных схем нередко (особенно в справочной литературе) электронные лампы и транзисторы рассматриваются как бесструктурные четырехполюсники с той или иной системой параметров (см. гл. 12).

Отличительной особенностью зависимых источников является их необратимость, т. е. цепи с этими источниками имеют четко выраженный вход и выход. Таким образом, для цепей с зависимыми источниками различают путь прямого прохождения сигнала (от входа к выходу) и обратного прохождения (с выхода на вход), реализуемого с помощью специальных цепей обратной связи (ОС) (гл. 14). Необходимость введения в активные цепи ОС объясняется рядом важных качеств, которыми эти цепи обладают: возможностью моделирования различных функций (см. § 2.7) (суммирование, интегрирование, дифференцирование и др.), генерированием и усилением колебаний, моделированием пассивных элементов типа R,L, Си их преобразованием (например, С и L), перемещение нулей и полюсов функции цепи (см. гл. 14, 15) и др.

 

1.3.Электрическая схема, топология электрической цепи

 

Кроме понятия электрической цепи в инженерной практике широкое распространение нашел термин «электрическая схема». В теории цепей схемойназывают графическое изображение электрической цепи. Элементам схемы соответствуют активные и пассивные элементы электрической цепи.

В микроэлектронике понятие электрической цепи и электронной схемы часто отождествляют между собой. Так, микросхемой(интегральной схемой) называют интегральную электрическую цепь, содержащую сотни и тысячи простейших активных и пассивных элементов. Чтобы не ломать сложившуюся традицию, будем использовать термин «электрическая схема» или просто «схема» применительно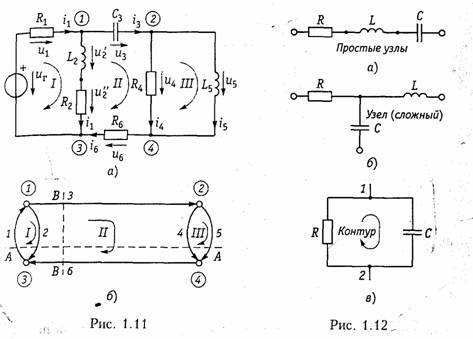

 



к графическому изображению электрической цепи или электронной схемы и термины «электрическая цепь» или «электронная (микроэлектронная, интегральная) схема» применительно к моделям реальных физических электрических или электронных устройств.

Для анализа электрических цепей в последнее время все большее распространение находят матрично-топологические методы.В их основе лежит представление электрической схемы с помощью графа цепи. Графом цепиназывают геометрическую систему линий (ветвей), соединяющих заданные точки (узлы). Если ветви графа ориентированы по направлению токов ветвей, то граф называется ориентированным(направленным). На рис. 1.11, аизображена электрическая схема и ее ориентированный (рис. 1.11, б) граф. Граф содержит всю информацию о геометрической структуре схемы.

Простым узломназывают место соединения зажимов двух элементов (рис. 1.12, «), а сложным — место соединения зажимов трех и более элементов (рис. 1.12, б).

Ветвьюназывают часть цепи, включенной между двумя узлами, через которые она обменивается энергией с остальной цепью. Ветви, подсоединенные к одной паре узлов, образуютпараллельное соединение(рис. 1.12, в).

Последовательно соединенные ветви, связывающие два заданиях узла образуют простой путь,если в нем нет повторяющих Узлов. Например, между узлами 1 и 4(рис. 1.11, б) простой путь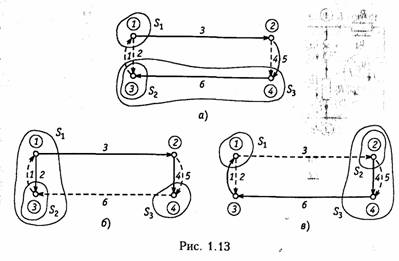



 

образуется ветвями 3, 5или 3, 4и т.д. Замкнутый путь называется контуром(рис. 1.12, в).

Подграфомназывают часть графа. Подграф является связным,если любые его два узла связаны, т. е. соединены ветвями.

Деревом графаназывают связный подграф, содержащий все узлы, но не содержащий ни одного контура (рис. 1.13). Ветви дерева называют ребрами(на рис. 1.13 показаны сплошными линиями).

В теории графов доказывается, что число ветвей дерева, содержащего «у узлов, определяется уравнением



Совокупность ветвей не входящих в состав дерева, образует его дополнение(на рис. 1.13 помечено штриховыми линиями). Ветви дополнения называют хордами.Можно показать, что число хорд



где п_в—общее число ветвей исходного графа.

Сечением графаназывают минимальное множество ветвей, удаление которых разбивает граф на две несвязанных части (подграфы). На рис. 1.11, 6показан пример двух сечений, образованных ветвями 1, 2, 4, 5(по линии А—А) и 3, 6(по линии В—В).Добавление любой из ветвей сечения делает граф связным. Обычно сечение изображают в виде замкнутой линии, рассекающей граф цепи на несвязанные компоненты. Сечение, «рассекающее» только одну ветвь дерева, называют главным сечением.Причем, каждому

дереву соответствует своя совокупность главных сечений (рис. 1.13, сечения S₁, S₂, S₃). Число главных сечений равно числу ветвей дерева (1.14).

Аналитически граф можно описать с помощью структурной матрицыА_с (матрицы соединений, инциденций), представляющей собой прямоугольную таблицу с числом столбцов, равным числу ветвей, и числом строк, равным числу узлов. Если положительное направление тока в ветви l выбрать от узла k,то элементы структурной матрицы аиопределяются из условия:



Анализ матрицы Ас: показывает, что сумма элементов каждого ее столбца равна нулю. Это является следствием зависимости одной из строк, поэтому ее можно исключить из А_c. Узел, строка которого исключается, называют базисным,а матрица А_o, образующаяся при этом, редуцированная.

Кроме матрицы Ас при анализе электрических цепей используется матрица сеченийС, представляющая собой таблицу со строками, соответствующими сечениям графа и столбцами — его ветвями.  Если за положительное направление принять направление ветви внутрь области, охваченной сечением, то элементы Матрицы сечений сыопределяются следующим образом:

 



 

Матрицей контуров В называют таблицу, с числом строк равным числу независимых контуров, и числом столбцов равным числу ветвей. Элементы матрицы контуров определяются по правилу



Число независимых контуров определяется числом хорд графа , (1.15).

 

1.4. Законы Кирхгофа

 

В теории цепей различают два типа задач: задачи анализа и синтеза электрических цепей. К задаче анализаотносятся все задачи, связанные с определением токов, напряжений или мощностей в элементах цепи, конфигурация и параметры которой известны. В задачах синтеза,напротив — известны токи и напряжения в отдельных элементах и требуется определить вид цепи и ее параметры, т. е. синтез является обратной задачей по отношению к анализу. Следует отметить, что задача синтеза существенно сложнее задачи анализа и будет рассмотрена в гл. 16.

В основе методов анализа электрических цепей лежат законы Кирхгофа.

Первый закон - закон токов Кирхгофа(ЗТК) формулируется по отношению к узлам электрической цепи и отражает тот факт, что в узлах не могут накапливаться заряды. Он гласит:алгебраическая сумма токов ветвей, сходящихся в любом узле электрической цепи, равна нулю.Формально это записывается так:



где т-число ветвей, сходящихся в узле.

В уравнении (1.16) токи, одинаково ориентированные относительно узла, имеют одинаковые знаки. Условимся знаки выходящих токов считать положительными, а входящих - отрицательными .Тогда,    например,   для   узла    1   схемы,    изображенной на рис. 1.11, a, согласно ЗТК — i₁+i₁ +iз = 0. Число независимых уравнений, составляемых по ЗТК, равно числу независимых узлов электрической цепи и определяется уравнением (1.14).

Закон токов справедлив и по отношению к сечениям электрической цепи. Покажем это на примере сечения Sз (рис. 1.13, а).Запишем ЗТК для узлов 1 и 2:

для узла 1: — i₁ + i₂+ iз ⁼ 0;

для узла 2: — iз + i₄+ i₅ = 0.

Сложив между собой эти уравнения, получим ЗТК для сечения 5з:

— i₁+ i₂+ i₄+i₅=0.

Второй закон — закон напряжений Кирхгофа(ЗНК) формулируется по отношению к контурам и гласит: алгебраическая сумма напряжений ветвей в любом контуре равна нулю:



где п -число ветвей, входящих в контур.

В уравнении (1.17) напряжения, совпадающие с направлением обхода контура, записываются со знаком «+», а не совпадающие — со знаком «—».

Составим, например, уравнение по ЗНК для цепи, изображенной на рис. 1.11, а.В соответствии с направлением для контура I:



Общее число линейно-независимых уравнений, составляемых по ЗНК, определяется числом независимых контуров, равных числу хорд (см. (1.15)).

Уравнение ЗТК и ЗНК можно записать в матричной форме, используя редуцированную структурную матрицу Ао и контурную матрицу В.

Закон токов получается путем перемножения матрицы Ао на матрицу-столбец токов ветвей:



 

l.5. Принцип эквивалентности.