ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 1 из 15

1.1.         Ток, напряжение, мощность

 

Понятия электрического тока и напряжения являются одними из основных в теории электрических цепей. Электрический токв проводящей среде есть упорядоченное движение электрических зарядов под воздействием электрического поля (ток проводимости в металлах, электролитах, газах; ток переноса в электровакуумных

приборах и др.).

Количественно электрический ток в каждый момент времени характеризуется скалярной величиной i= i(t) — мгновенным значением тока,характеризующим скорость изменения заряда qво времени:



где Δq— электрический заряд, прошедший за время Δtчерез поперечное сечение проводника. В системе СИ заряд измеряется в кулонах (Кл), время — в секундах (с), ток — в амперах (А). В дальнейшем для краткости электрические токи и напряжения будем просто называть токами и напряжениями.

В соответствии с приведенным выше определением понятие «ток» может использоваться в двух смыслах: ток как физический процесс и ток как количественная характеристика (вместо «силы

тока»).

Как функция времени ток i(t)может принимать положительные и отрицательные значения. Принято считать значение тока i(t)положительным, если движение положительно заряженных частиц совпадает с заранее выбранным направлением отсчета тока и отрицательным — в противном случае. Выбор направления отсчета тока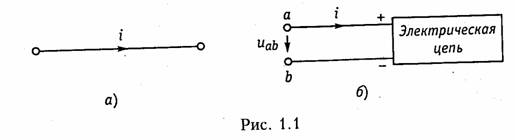



произволен, положительное направление отсчета тока показывается стрелкой (рис. 1.1).

Электрическое напряжениемежду двумя точками электрической цепи определяется количеством энергии, затрачиваемой на перемещение единичного заряда из одной точки в другую: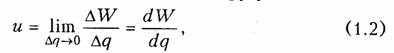



где W— энергия электрического поля. Единица измерения напряжения в системе СИ — вольт (В), энергии — джоуль (Дж).

В потенциальном электрическом поле напряжение между двумя точками совпадает по значению с разностью потенциалов между ними. Например, напряжение между точками аи bцепи, показанной на рис. 1.1, б,



где V_aи Vb—потенциалы точек аи b.

Значение напряжения в любой заданный момент tназывается мгновенными обозначается и = и (t).Являясь скалярной величиной, u(t)может принимать как положительные, так и отрицательные значения. Для однозначного определения знака напряжения выбирают положительное направление его отсчета, которое показывается стрелкой (рис. 1.1, б),направленной от одной точки электрической цепи к другой. Для определенности будем считать, что положительное направление отсчета совпадает с направлением стрелки от более высокого потенциала, т. е. «+», к более низкому, т. е. «—» (рис. 1.1, б).При этом положительные направления отсчета напряжения и тока будут между собой согласованы,так как положительное направление отсчета напряжения и₍,ьсоответствует направлению перемещения положительно заряженных частиц от более высокого потенциала V_a(+)к более низкому V_b(-).Очевидно, что u_ab= —u_ba.Применительно к напряжению на участке цепи, по которому протекает ток, часто используют термин «падение напряжения».

Электрическая энергия,затраченная на перемещение единичного положительного заряда между двумя точками участка цепи с напряжением и(разностью потенциалов) к моменту времени tопределится согласно (1.1) и (1.2) уравнением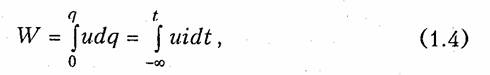



где принято W=0при t= —∞.

Производная энергии по времени определяет мгновенную мощность,потребляемую элементами, входящими в участок цепи:



Мощность измеряется в ваттах (Вт). Знак мощности ропределяется знаком напряжения и тока. Если р>0, мощность потребляется элементами участка цепи,а при р<0 — отдается.

По характеру изменения во времени различают постоянные, гармонические, периодические несинусоидальные, непериодические токи и. напряжения. В ряде случаев (например, в цепях с распределенными параметрами) токи и напряжения могут быть не только функциями времени, но и функциями пространственных координат. В технике связи токи и напряжения как материальные носители сообщений называют сигналами.

 

1.2. Электрическая цепь, ее элементы и модели

 

Электрической цепьюназывают совокупность устройств, предназначенных для прохождения тока п описываемых с помощью понятий тока п напряжения. Электрическая пень состоит из источников (генераторов) и приемников электрической энергии.

Источникомназывают устройство, создающее (генерирующее) токи п напряжения. В качестве источников могут выступать как первичные устройства, преобразующие различные виды энергии в электрическую (аккумуляторы, электромашинные генераторы, термоэлементы, пьезодатчики п т. д.), так и устройства, преобразующие электрическую энергию первичных источников в энергию электрических колебаний требуемой формы.

Приемникомназывают устройство, потребляющее (запасающее) пли преобразующее электрическую энергию в другие виды энергии (тепловую, механическую, световую и т. д.). Физическими элементами реальной электрической цепи являются резисторы, катушки индуктивности, конденсаторы, трансформаторы, транзисторы, электронные лампы и другие компоненты электроники. При этом электрическая цепь может конструктивно выполняться либо из указанных выше дискретных компонентов, либо изготовляться в едином технологическом цикле (интегральные схемы). Электрические цени, содержащие как интегральные, так и дискретные компоненты, получили наименование гибридных.

В основе теории электрических цепей лежит принцип моделирования.При этом реальные электрические цепи заменяются некоторой идеализированной моделью, состоящей из взаимосвязанных идеализированных элементов. Последние представляют собой простые модели, используемые для аппроксимации (приближения) свойств простых физических элементов или физических явлений. В зависимости от точности приближения одна и та же физическая электрическая цепь может быть представлена различными моделями, причем, чем точнее модель, тем она сложнее. На практике обычно ограничиваются  наиболее простыми  моделями,  обеспечивающими решение задач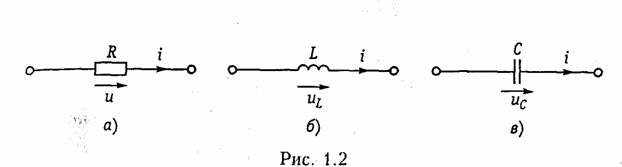



анализа и синтеза реальной цепи с заданной точностью. Важно иметь в виду, что если физические элементы и явления могут быть описаны лишь приближенно, то идеализированные элементы определяются точно. К простейшим идеализированным элементам модели электрической цепи относятся независимые и зависимые источники (активные элементы) и элементы резистивного сопротивления, индуктивности и емкости (пассивные элементы).

Систему уравнений, описывающую модель электрической цепи, называют математической моделью цепи.В теории электрических цепей изучаются общие свойства моделей цепей, поэтому в дальнейшем под электрической цепью будем понимать ее модель, свойства которой близки к свойствам реальной физической цепи.

Пассивные элементы.Резистивным сопротивлениемназывают идеализированный элемент, обладающий только свойством необратимого рассеивания энергии. Условное обозначение резистивного сопротивления показано на рис. 1.2, а.Математическая модель, описывающая свойства резистивного сопротивления, определяется законом Ома:



Коэффициенты пропорциональности Rи G в формулах (1.6) называются соответственно сопротивлениеми проводимостьюэлемента и являются его количественной характеристикой, причем при согласованных направлениях тока и напряжения Rи G положительны и связаны обратной зависимостью R= 1/G.Измеряют в системе СИ сопротивление Rв омах (Ом), а проводимость G— в сименсах (См).

Уравнение (1.6) определяет зависимость напряжения от тока и носит название вольт-амперной характеристики(ВАХ) резистивного сопротивления. Если Rпостоянно, то ВАХ линейна (рис. 1.3, а)и соответствует линейному резистивному элементу. Если же Rзависит от протекающего через него тока или приложенного к нему напряжения, то ВАХ становится нелинейной (рис. 1.3, б) и соответствует нелинейному резистивному сопротивлению.

Мощность в резистивном сопротивлении можно определить согласно уравнению (1.5):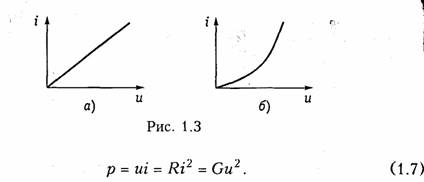

 



Мощность в резистивном сопротивлении всегда больше нуля, так как оно только потребляет энергию, преобразуя ее в тепло или другие виды энергии.

Индуктивным элементомназывают идеализированный элемент электрической цепи, обладающий только свойством накопления им энергии магнитного поля. Условное обозначение индуктивного элемента изображено на рис. 1.2, б.

Математическая модель, описывающая свойства индуктивного элемента определяется соотношением



где ψ—потокосцепление, характеризующее суммарный магнитный поток, пронизывающий катушку: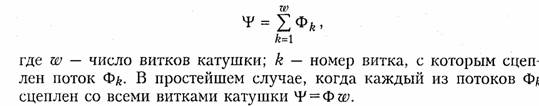



Коэффициент пропорциональности Lв формуле (1.8) называется индуктивностью.Он имеет положительное значение и является количественной характеристикой индуктивного элемента. Измеряется индуктивность Lв генри (Гн), а магнитный поток Ф — в веберах (Вб). Если величина Lпостоянна, то зависимость (1.8); {вебер-амперная характеристика}линейна и соответствует линейному индуктивному элементу. Если же Lзависит от электрического режима (тока или напряжения), то зависимость (1.8) нелинейна и соответствует нелинейному элементу индуктивности.           

Связь между током и напряжением на индуктивном элементе определяется согласно закону электромагнитной индукции выражением      



т. е. напряжение на индуктивном элементе пропорционально скорости  изменения протекающего через  него тока.   Следовательно, при протекании через Lпостоянного тока u = 0 и свойства индуктивного элемента эквивалентны коротко замкнутому (КЗ) участку (_См. рис. 1.1, а).

Мгновенная мощность электрических колебаний в индуктивном элементе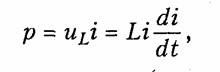



т.е.может быть как положительной (при совпадении направлений ии i),так и отрицательной (при несовпадении направлений ии i). Причем в первом случае (р>0) магнитная энергия запасается индуктивным элементом, а во втором (р<0) —отдается во внешнюю цепь.

Энергия, запасенная в индуктивном элементе к моменту t,определится согласно (1.4)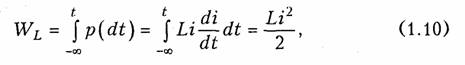



т. е. всегда полoжительна.

Емкостным элементом называютидеализированный элемент электрической цепи, обладающий только свойством накапливать энергию электрического поля. Условное обозначение емкостного элемента показано на рис. 1.2, в.

Математическая модель, описывающая свойства емкостного элемента, определяется вольт-кулонной характеристикой

q=Cu_c.                                    (1.11)

Коэффициент пропорциональности С в формуле (1.11) называется емкостьюи является количественной характеристикой емкостного элемента. При согласованных направлениях тока и напряжения величина С всегда положительна. Измеряется С в фарадах (Ф).

Если величина С постоянная, то вольт-кулонная характеристика (1.11) линейна и соответствует линейному емкостному элементу. Если же параметр С зависит от электрического режима, то характеристика (1.11) нелинейна и соответствует нелинейному элементу.

Между током и напряжением на емкостном элементе существует связь, определяемая согласно (1.1) и (1.11) равенством



т. е. ток в емкостном элементе пропорционален скорости изменения приложенного к нему напряжения. При постоянном напряжении и=const, i = 0 и емкостной элемент по своим свойствам эквивалентен разрыву цепи.

Мощность электрических колебаний в емкостном элементе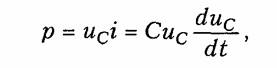



т. е. может быть как положительной, так и отрицательной в зависимости от направлений тока и напряжения. При р>0 энергия электрического поля запасается емкостным элементом, а при р<0 — отдается во внешнюю цепь.

Энергия, запасенная в емкостном элементе к моменту t,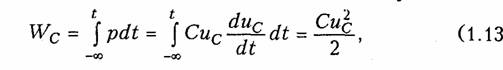



т. е. всегда положительна.

В инженерной практике резистивное сопротивление, индуктивный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя, по существу, элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумениям, также будем пользоваться этой терминологией.   

Рассмотренные идеализированные резистивный, индуктивный и емкостной элементы могут служить простейшими моделями резисторов, высококачественных' катушек индуктивностей с малыми потерями и электрических конденсаторов с высокими диэлектрическими свойствами в области низких и средних частот. В области высоких, а особенно сверхвысоких частот модели резисторов, катушек индуктивности и конденсаторов становятся более сложными.Так, на высоких частотах резисторы уже нельзя с достаточной точностью описать идеальным резистивным элементом (1.6) из-за влияния различных «паразитных» емкостей.  Более точной здесь будет модель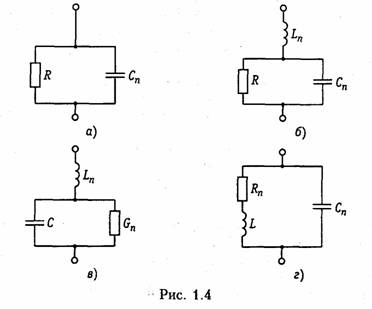



параллельного соединения Rи С_П,изображенная на рис. 1.4, а.В некоторых случаях возникает необходимость учета, «паразитной» индуктивности L_П,учитывающей эффект накопления энергии магнитного поля в элементах резистора (рис. 1.4, б).

На высоких и сверхвысоких частотах также начинает проявляться поверхностный эффект, выражающийся в неравномерном распределении тока по сечению проводника {скип-эффект).В результате этого сопротивление Rпроводника начинает расти с увеличением частоты. Причем, чем толще проводник, тем при меньших частотах начинает проявляться скип-эффект. На сверхвысоких частотах зависимость сопротивления круглого медного проводника от частоты fможно выразить эмпирической формулой



где Ro— сопротивление проводника постоянному току, Ом; d— диаметр сечения проводника, мм; f—частота, МГц.

Модель конденсатора, кроме емкостного элемента С, может содержать параллельную проводимость G_П, учитывающую потерн , энергии в диэлектрике, и последовательную индуктивность L_П, учитывающую эффект запасения энергии магнитного поля в конструктивных элементах конденсатора (рис. 1.4, в).

Модель катушки индуктивности может учитывать потери энергии в проводе и энергию электрического поля, запасаемую между витками катушки путем дополнительного включения сопротивления потерн R_Пи «паразитной» емкости С_П (рис. 1.4, г).

В зависимости от условий применения и конструктивных особенностей, требований к точности анализа могут использоваться и более сложные модели резисторов, катушек индуктивностей и конденсаторов.

В зависимости от соотношения между длинами цепи lи волны тока п напряжения λ различают цепи с сосредоточенными и распределенными параметрами.При l<λможно считать, что параметры R,L, Ссосредоточены в резисторах, катушках индуктивности и конденсаторах; при l>> λнеобходимо пользоваться моделью цепи с распределенными параметрами (см. гл. 13).

Рассмотренные выше резистивные индуктивные и емкостные элементы относятся к двухполюсным,так как содержат только два зажима (полюса, вывода). Однако кроме двухполюсных элементов в теории цепей и электронике широко используются трехполюсные, четырехполюсныеи многополюсные элементы.Например, свойства трансформатора как физического устройства, содержащего две индуктивно связанные катушки, не могут быть описаны моделью только двухполюсных элементов с индуктивностями L₁ и L₂. Для его моделирования необходимо введение еще одного параметра  —  взаимной   индуктивности  М;  при  этом  моделью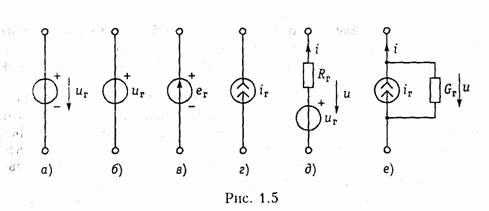



трансформатора  будет  являться  четырехполюсный  элемент  (см. гл. 3).