ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 4 из 15

Пример.Рассчитать токн ветвей схемы резнстнвноп цепи, изображенной на рис. 2.1. апо методу уравнений Кирхгофа.

Построим граф цепи (рис. 2.1, б) и выберем дерево (рис. 2.1, в). Дополним дерево хордами 2,5, 6(на рис. 2.1, в показано пунктиром). В результате образуется три независимых контура I,II, III(рис. 2.1, я). Составим уравнение по ЗТК и ЗНК.

Схема имеет n_y= 4 узла, п_B=6 ветвей. Выберем узел 4в качестве базисного и составим n_у = 3 уравнения по ЗТК: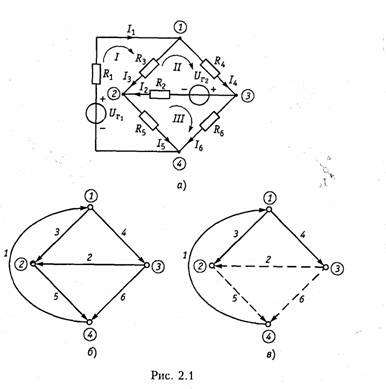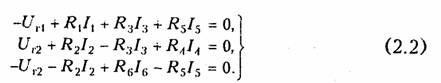







 

Решая совместно системы уравнений (2.1) и (2.2), найдем искомые токи.

При использовании законов Кирхгофа в качестве независимых переменных можно было взять напряжения ветвей (метод напряжения ветвей)или токи одних ветвей и напряжения других (гибридный метод).

В случае, если в цепи имеется ветвь с источником тока, то неизвестным параметром в этой ветви является напряжение на зажимах источника, которое можно найти методом напряжения ветвей.

 

1.12. Преобразование резистивных электрических цепей

 

В случае, когда на цепь воздействует один источник постоянного напряжения или тока, наиболее эффективным является метод преобразования электрических цепей. Суть этого метода заключается в нахождении эквивалентного сопротивления цепи относительно зажимов (полюсов) источника.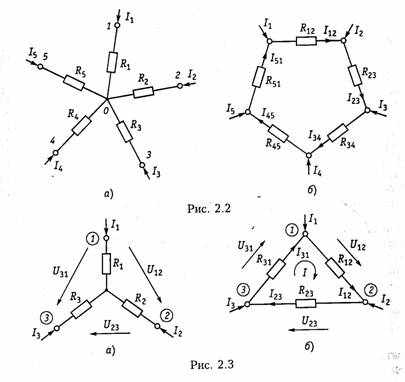

 



В § 1.5 были рассмотрены простейшие методы преобразования последовательного и параллельного соединенных пассивных элементов (см. формулы (1.22) —(1.24) и (1.27) —(1.29)). Однако на практике встречаются более сложные соединения элементов, которые нельзя свести только к последовательному или параллельному. Примером подобного соединения являются соединения многолучевой звездой (рис. 2.2, а)и многоугольником (рис. 2.2, б).

Характерной особенностью этих соединений является наличие внутреннего узла 0 в звезде и внутреннего контура в многоугольнике. Наиболее часто встречаются случаи трехлучевой звезды и треугольника (рис. 2.3, а,б).

Найдем формулы преобразования соединения «треугольника» в «звезду». Запишем для схемы «треугольник» уравнения по ЗТК и ЗНК (рис. 2.3, б):



Уравнения (2.6) и (2.7) позволяют осуществить переход от соединения резистивных элементов «треугольник» к соединению «звезда». Обратный переход можно получить по формулам



Пример.Рассчитать токи ветвей схемы резистивной цепи, изображенной на рис. 2.4, а.Данная схема может служить моделью измерительного моста, который находит широкое применение в различных измерительных приборах, в частности для измерения сопротивлений. Принцип работы моста основан на выполнении условий баланса его плечей.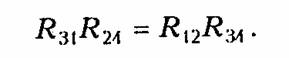



При этом потенциалы узлов 2и 3оказываются одинаковыми и в диагонали моста R₂₃ ток будет равен нулю. Таким образом, если включить в диагональ моста вместо R₂₃измерительный прибор — амперметр, то путем изменения одного из сопротивлений плеча (например, R₂₄с помощью магазина сопротивлений), можно найти сопротивление другого (например R_3l). Для случая, когда R₁₂ ⁼ RM₃₁⁼ R,условие баланса достигается при R₃₄= R₂₄.

Преобразуем треугольник R_12,R_23,R₁₃в звезду с лучами R₁,R_2,R₃(рис. 2.4, б), где R₁,R₂,R₃определяются формулами (2.6) и (2.7). Тогда эквивалентное сопротивление цепи относительно зажимов источника (узлы 1 и 4)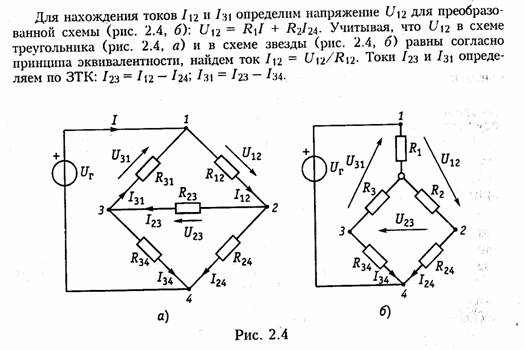





Аналогично формуле (2.9) можно получить формулыпреобразования n-лучевой звезды в полный многоугольник с числом ветвей равным п_в= п(п —1)/2:



Следует отметить, что обратная задача преобразования многоугольника в эквивалентную n-лучевую звезду при n>3 не имеет решения, так как при этом оказывается число уравнений п(п —1)/2 превышает число неизвестных.

 

1.13. Метод наложения

 

В основе метода наложения лежит принцип суперпозиции (наложения), линейных электрических цепей (§ 1.6). Этот метод применяется в случае, когда в цепи действует несколько источников напряжения или тока. При этом в соответствии с этим принципом находят частичные токи и напряжения, а результирующие реакции определяются путем алгебраического суммирования частичных токов и напряжений.

Проиллюстрируем принцип наложения на примере резистивной цепи, изображенной на рис. 2.5, а,содержащей идеальные источники напряжения. Найдем ток в резистивном элементеR3.Положим вначале, что в цепи действует только один источник U_T\;второй источник напряжения исключается и зажимы его закорачиваются. При этом получаем частичную схему, изображенную на рис. 2.5, 6.Определим ток Iз' от воздействия напряжения U_Г1'.





Теперь полагаем, что в цепи действует только источник U_Г2- Исключив источник U_Г1,получим вторую частичную схему (рис. 2.5, в).Ток Iз" от воздействия U_Г2определится как



Результирующий ток Iз найдем как алгебраическую сумму частичных токов Iз ' и Iз ": Iз = Iз’+ Iз ".При определении результирующих токов знак «+» берут у частичных токов, совпадающих с выбранным положительным направлением результирующего тока, и знак «—» — у несовпадающих. Как следует из рассмотренного примера, при составлении частичных электрических схем исключаемые идеальные источники напряжения закорачиваются. В случае, если в цепи действуют источники напряжения с внутренними сопротивлениями R_Г,при их исключении они заменяются своими внутренними сопротивлениями R_Г.

При наличии идеальных источников тока соответствующие ветви исключаемых источников размыкаются, а при наличии реальных источников они заменяются своими внутренними проводимостями G_r.

Пример.Определить ток /з в цепи, изображенной на рис. 2.6, а.Составляем две частные схемы (рис. 2.6, б, в),для которых находим частичные токи: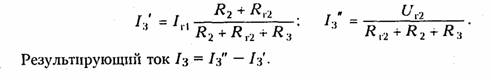



При наличии в цепи зависимых источников они остаются в частичных схемах неизменными.                                                  

1.14. Метод контурных токов

При определении токов и напряжений в отдельных ветвях цепи с n_B -ветями по законам Кирхгофа в общем случае необходимо решить систему из п_вуравнений. Для снижения числа решаемых уравнений и упрощения расчетов используют методы контурных токов и узловых напряжений.

Метод контурных токовпозволяет снизить число решаемых уравнений до числа независимых контуров, определяемых равенством (1.15). В его основе лежит введение в каждый контур условного контурного тока Ik,направление которого обычно выбирают совпадающим с направлением обхода контура. При этом для контурного тока будут справедливы ЗТК и ЗНК. В частности, для каждого из выделенных контуров можно составить уравнения по ЗНК. Поясним суть метода контурных токов на примере резистивной цепи, схема которой изображена на рис. 2.5, а.Для контурных токов Iк₁ и I_К2 этой схемы можно записать уравнения по ЗНК в виде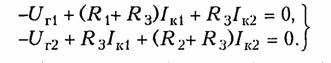



Перенесем U_T\и U_r2в правую часть системы и получим так называемую каноническую формузаписи уравнений по методу контурных токов:



Слагаемые  в уравнении (2.11) берутся со знаком «+», если ток I_кl и I_кпобтекают Rl_nв одном направлении и со знаком «—» в противном случае. Контурное задающее напряжениеU_Kравно алгебраической сумме задающих напряжений источников, входящих в каждый контур. Со знаком «+» суммируются источники, задающее напряжение которых направлено навстречу контурному току, и со знаком «—», если направление напряжения и контурного тока совпадают.

Решая систему уравнений (2.11), найдем значения контурных токов



Как следует из уравнений (2.14) и (2.15), контурный ток может быть получен алгебраическим суммированием частичных токов от воздействия каждого контурного задающего напряжения в отдельности. Таким образом, полученный результат отражает рассмотренный в § 1.6 принцип наложения.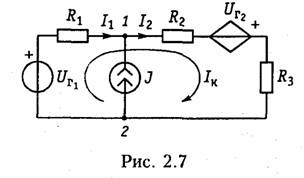



Если в схеме кроме источников напряжения содержится п-ветвей с источниками тока, то независимые контуры выбираются так, чтобы источник тока входил только в один контур. Это можно сделать, если выбрать дерево графа цепи таким, чтобы источник тока   входил   в   одну   из   хорд.

Число контурных уравнений при этом уменьшается до



Напряжения от задающих токов этих источников учитываются в левой части системы (2.11) на взаимных сопротивлениях, которые эти токи обтекают. Например, для схемы, изображенной на рис. 2.6, а,составляется только одно уравнение для II контура:

 

 



Сформулированные выше правила составления уравнений по методу контурных токов справедливы и в случае зависимых источников напряжения ИНУН и ИНУТ.

Пример.Найдем токн в цепи содержащей ИНУТ с задающим напряжением U_г2 =  HRI₁(рис. 2.7) по методу контурных токов.

Учитывая, что цепь содержит ветвь с идеальным независимым источником тока J согласно (2.15) составим всего одно уравнение для контурного тока I_к. При этом задающий ток источника тока J замыкаем по ветви с R₁и U_Г1,в результате получим



 

 

где I_К — матрица-столбец контурных токов. Подставляя (2.19) в (2.18), получаем:

BR_BB^TI_K =BU_ГB.                                   (2.21)

Если учесть, что

BR_BB^T=R_K,   Ви_ГВ=U_к,(2.22)

где R_K — квадратная матрица контурных сопротивлений; U_K — матрица-столбец контурных задающих напряжений, то в соответствии с (2.20) получим матричное уравнение контурных токов

R_KI_K=U_K.(2.23)

Пример.Рассмотрим схему, изображенную на рис. 2.8, а.В соответствии с направлением токов строим направленный граф цепи (рис. 2.8, б) и дерево графа (рис. 2.8, в).Подсоединяя к дереву хорды (на рис. 2.8, гобозначены пунктиром), получаем три независимых контура. Выбрав направление обхода контуров I, II и III,в соответствии с правилом, изложенным в § 1,3, строим контурную матрицу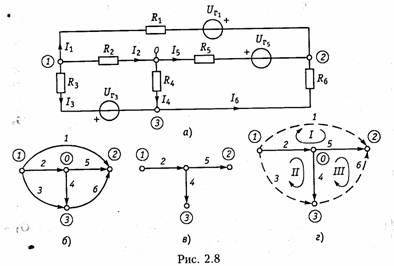



 



Для линейных электрических цепей важную роль играет принцип взаимности (теорема обратимости).Он гласит: если источник напряжения, помещенный в какую-либо ветвьIпассивной линейной электрической цепи, вызывает в другой ветвиkток определенного значения, то этот же источник, будучи помещенный в ветвьk, вызывает в ветвиlток с тем же значением.Справедливость этого принципа следует непосредственно из уравнений (2.14) и (2.15) с учетом того, чтоΔlk = Δkl.

 

1.15. Метод узловых потенциалов

 

Метод узловых потенциалов (узловых напряжений) является наиболее общим и широко применяется для расчета электрических цепей, в частности, в различных программах автоматизированного проектирования электронных схем.

Метод узловых потенциаловбазируется на ЗТК и законе Ома. Он позволяет снизить число решаемых уравнений до величины, определяемой равенством (1.14). В основе этого метода лежит расчет напряжений в (n_у — 1)-м узле цепи относительно базисного узла. После этого на основании закона Ома находятся токи или напряжения в соответствующих ветвях. Рассмотрим сущность метода узловых потенциалов на примере резистивной цепи, изображенной на рис. 2.9, а.Примем потенциал Vз ⁼ 0 (базисный узел) и с помощью (1.31) преобразуем источники напряжения в эквивалентные источники тока





Проводимости G₁₁ и G₂₂ представляют собой арифметическую сумму проводимостей всех ветвей, подсоединенных соответственно к узлам 1 и 2; они называются собственными проводимостямиузлов 1 и 2. Проводимости G₁₂ = G₂₁ равны арифметической сумме проводимостей всех ветвей, включенных между узлами 1 и 2, и называются взаимными проводимостямиузлов 1 и 2. Алгебраическую сумму задающих токов I_y1и I_У2 источников тока подключенных соответственно к узлам 1 и 2 называют задающими узловыми токамиузлов 1 и 2. Задающие токи источников в алгебраической сумме берутся со знаком «+», если положительное направление задающего тока источника ориентировано к соответствующему узлу, и «—», если от узла. Например, для узлового тока I_y1 со знаком «+» берется ток I_Г1 так как ориентирован по направлению к узлу 1, и знак «—» берется для I_Г2,так как он ориентирован от узла 1.

Решив систему (2.26) относительно V₁и V₂определим узловые потенциалы цепи. Искомые токн находим по закону Ома.

Полученный результат можно обобщить на произвольную резистивную схему с пузлами. Если принять п-йузел за базисный, то система уравнений по методу узловых потенциалов приобретает вид



Из уравнений (2.29) так же как из уравнений (2.14), следует, что   узловые   потенциалы   определяются   алгебраической   суммой



частичных узловых потенциалов, обусловленных действием каждого задающего узлового тока в отдельности, т. е. как и в методе контурных токов уравнения (2.29) отражают принцип наложения, характерный для линейных электрических цепей.

Рассмотренный   метод   составления узловых напряжений справедлив и при наличии в цепи зависимых источников типа ИТУТ и ИТУН. В цепи, изображенной на рис. 2.10, содержится кроме независимого источника напряжения U_Г1зависимый ИТУН с задающим током Jз = = HGU₁.Определим токи в цепи методом узловых потенциалов.

В соответствии с вышеизложенным 'методом примем за базисный узел V₂=0. Тогда для узла / получим



 

Запишем уравнение по метолу узловых потенциалов в матричной форме. Умножим элементы редуцированной структурной матрицыАо на потенциалы Vсоответствующих узлов, в результате получим матрицу напряжения ветвей:



Умножим левую и правую часть матричного уравнения (2.17) на матрицу Ао и учитывая ЗТК в матричной форме (1.18) и равенство (2.30), получим



получим матричную форму уравнений равновесия узловых потенциалов:



где Gy — квадратная матрица узловых проводимостей, I_у — матрица-столбец узловых токов.