ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 6 из 15

Емкостные цепи.Для емкостного элемента согласно уравнению (1.12) имеем: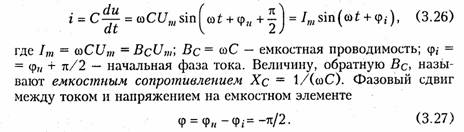



Из приведенных уравнений следует, что ток в емкости опережает приложенное напряжение на угол π/2 (рис. 3.6, в),причем знак «—>> свидетельствует об отставании напряжения иот тока i. Средняя за период мощность в емкостной цепи также равна нулю.

При последовательном и параллельном соединениях емкостных элементов ток в цепи определяется согласно (3.26), где С находится из (1.24) для последовательного и (1.28) для параллельного соединений.

 

2.4. Гармонические колебания в цепи при последовательном соединенииR,L,С-элементов

 

Допустим, что в цепи, содержащей последовательно соединенные элементы R,L, С(рис. 3.7), протекает ток



На рис. 3.8 изображена векторная диаграмма напряжений, описываемых уравнений (3.30).

Напряжение U_MRна резистивном сопротивлении Rназывается активной составляющей приложенного напряженияи обозначается 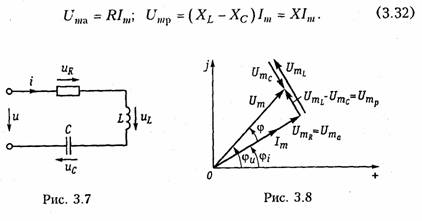 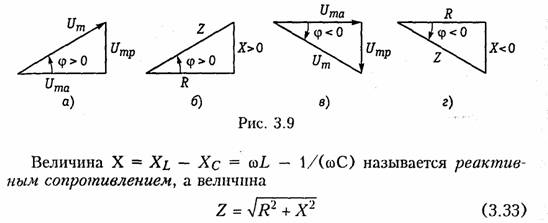разность напряжений называется реактивной составляющей.Согласно этому определению и формулам (3.31) имеем:





— полным сопротивлением цепи.

Треугольник на векторной диаграмме, образованный напряжениями U_ma,U_mp,U_mназывают треугольником напряжений.Если U_mL>U_mc(XL>Xc),то цепь носит индуктивный характер (приложенное напряжение опережает ток) и треугольник напряжений имеет вид, изображенный на рис. 3.9, а;если U_mL<U_mc(XL< Хс),то цепь носит емкостный характер (приложенное напряжение отстает от тока) и треугольник напряжений принимает вид, изображенный на рис. 3.9, в.Треугольник со сторонами R,X,Zподобный треугольнику напряжений, называетсятреугольником сопротивлений(рис. 3.9, б, г).Из треугольников сопротивлений и напряжений следует: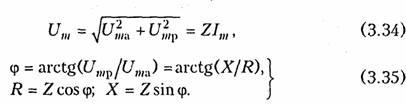



 

 

Треугольники напряжений и сопротивлений позволяют упростить анализ электрической цепи.

2.5. Гармонические колебания в цепи при параллельном

 соединенииR,L,С-элементов

Приложим к цепи, содержащей параллельно соединенные элементы R,L,С (рис. 3.10), напряжение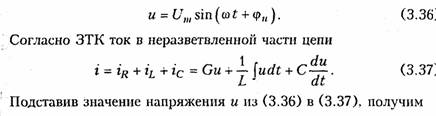





На рис. 3.11 изображена векторная диаграмма токов, описываемых уравнением (3.39).

Ток в резистивном сопротивлении I_тRназывают активной составляющейтока I_та, а разность тока I_тр = I_тL— 1_тс — реактивной составляющей тока.Для I_тaи I_тр справедливы соотношения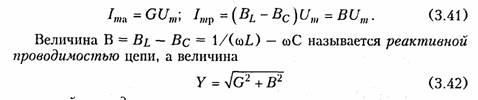



— полной проводимостью цепи.

По аналогии с треугольником напряжений и сопротивлений при параллельном соединении элементов можно ввести треугольники токов и проводимостей(рис. 3.12, а, б).Как следует из этих ри-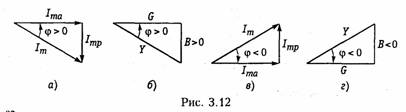



сунков, при I_тL>ImC(B_L>B_C)цепь носит индуктивный характер (общий ток отстает от приложенного напряжения) и при I_тL<I_mc(B_L<B_C) —емкостный характер (ток опережает приложенное напряжение). Из треугольников токов и проводимостей следует: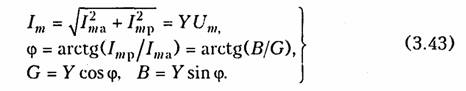



Сравнение треугольников токов и проводимостей с треугольниками напряжений и сопротивлений показывает их дуальный характер. Дуальны также и все соотношения, описывающие цепи при последовательном и параллельном соединении элементов, дуальны и сами цепи.

 

2.6. Символический метод расчета разветвленных цепей

 

Расчет разветвленных цепей при смешанном соединении элементов в режиме гармонических колебаний обычно осуществляется символическим методом. Это объясняется тем, что классический метод расчета приводит к громоздким интегрально-дифференциальным уравнениям и требует большого объема тригонометрических преобразований. Символический методпозволяет тригонометрические операции над гармоническими колебаниями и геометрические операции над векторами свести к алгебраическим операциям над комплексными числами, что существенно упрощает расчет. При этом могут быть использованы все методы преобразований и анализа, изложенные в гл. 1, 2. Допустимость использования символического метода объясняется тем, что в линейных цепях в режиме гармонических воздействий в цепи устанавливаются гармонические колебания тон же частоты. Таким образом, неизвестными параметрами токов и напряжений будут лишь амплитуды и фазы, определяемые однозначно их комплексными амплитудами. Запишем основные законы электрических цепей в символической форме.

Для резистивного элемента Rсвязь между комплексными амплитудами тока I_т и напряжения U_т можно определить согласно закону Ома (1.6) путем замены мгновенных значений токов iи напряжений иих комплексными амплитудами: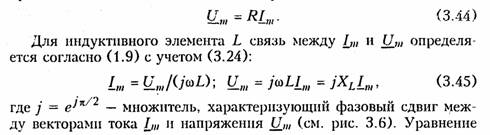



(3.45) отражает закон Ома для индуктивных элементов. Сравнение (3.45) с (1.9) показывает, что операция дифференцирования d/dtсоответствует в комплексной форме умножению на jω.

Для емкостного элемента С на основании (1.12) можно записать:



т. е. операция интегрирования соответствует в комплексной форме делению на/со. Полученные уравнения (3.44) —(3.46) справедливы и для комплексных действующих значений токов и напряжений: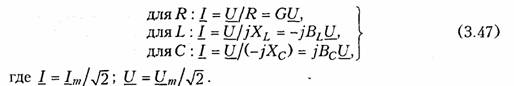



Аналогично можно получить уравнения законов Кирхгофа в комплексной форме. Так, для ЗТК (1.16) заменив мгновенные значения токов i_kих комплексными амплитудами I_mk,получим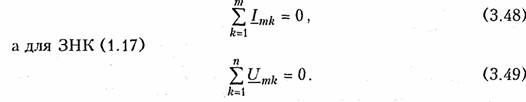



Полученные уравнения законов Ома и Кирхгофа в комплексной форме лежат в основе символического метода расчета линейных цепей при гармонических воздействиях. Причем, как показывает анализ уравнений (3.24), (3.26). (3.45) и (3.46), при переходе к комплексной записи операции дифференцирования заменяются умножением на jω, операции интегрирования — делением на jω. В результате вместо системы интегрально-дифференциальных уравнений получаем систему алгебраических уравнений, решение которой определяет амплитуды и начальные фазы искомых токов и напряжений.

Применим символический метод к анализу гармонических колебаний в цепи при последовательном (см. § 3.4) и параллельном (см. § 3.5) соединениях элементов R, L,С.Для последовательного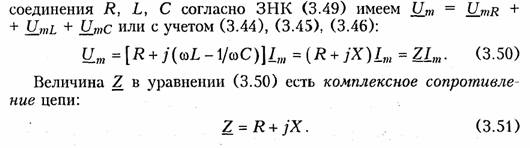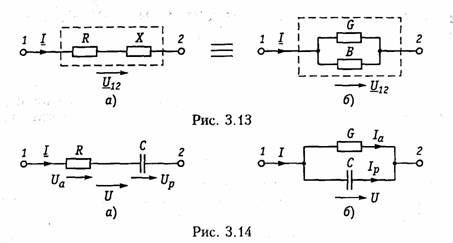





Комплексное сопротивление Z можно выразить в показательной или тригонометрической форме:



Таким образом, рассмотренное ранее полное сопротивление цепи (3.33) представляет собой модуль комплексного сопротивления:



а фазовый сдвиг φ — аргумент (arg) комплексного сопротивления:



Аналогичным образом можно получить уравнения токов и напряжений в комплексной форме для параллельного соединения элементов R,L, С(см. § 3.5). Так уравнение (3.39) в комплексной форме примет вид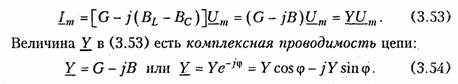



Следовательно, полная проводимость цепи Y равна модулю комплексной проводимости Y = | Y‌‌‌‌‌‌‌|, а фазовый сдвиг φ — аргументу комплексной проводимости φ= arg Y= arctg(B/G).

При анализе различных электрических цепей часто возникает необходимость преобразования схемы последовательно соединенных элементов в эквивалентное параллельное соединение и наоборот (рис. 3.13). В основе подобных преобразований лежит принцип эквивалентности (см. § 1.5). Согласно этому принципу ток I и напряжение U₁₂в исходной (рис. 3.13, а)и преобразованной (рис. 3.13, б) схемах должны остаться неизменными. Для первой



Преобразование (3.56) и (3.57) можно положить в основу разложения тока в последовательном участке и напряжения в параллельном на активную и реактивную составляющие.

Пример.Преобразовать последовательный RC-участок(рис 3.14, я) в эквивалентный параллельный (рис. 3.14, б). Определить активные и реактивные составляющие токов и напряжений на обоих участках.

В соответствии с уравнением (3.57) получаем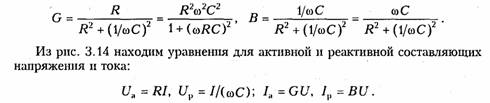



Символический метод особенно эффективен при анализе сложных разветвленных цепей. Причем поскольку все методы расчета подобных цепей (метод контурных токов, узловых потенциалов, наложения и др.) базируются на законах Ома и Кирхгофа, то эти методы могут использоваться и при комплексной форме с заменой соответствующих величин (токов, напряжений, сопротивлений, проводимостей) их комплексными значениями.

Пример.Проиллюстрируем это на примере расчета цепи, изображенной на рис. 3.15 различными методами в комплексной форме. Заменим элементы ветвей в исходной схеме их комплексными сопротивлениями, а источники напряжения и токи их комплексными значениями (рис. 3.16):



Рассчитаем теперь эту цепь различными методами в символической форме, используя комплексы действующих значений токов и напряжений.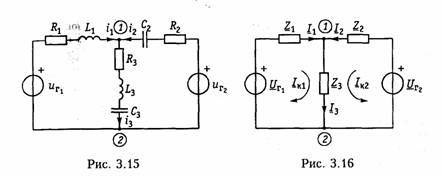



1.   Метод наложения.  Сравнение схем,   изображенных  на рис.   3.16  и рис. 2.5. а показывает их одинаковую топологию. Таким образом, путем перехода от Rк Z, от U_rк U_rи от I к Iможно сразу получить соответствующие уравнения для токов I _1,I _2,I ₃(см. § 2.3).

2.  Метод контурных токов.В соответствии с § 2.4 составляем систему из двух уравнений для контуров I и II:



 

писать уравнения для мгновенных значений iи и.Так, если угловая частота задающих источников синусоидальных колебаний u_r1и u_r2 равна ω, то мгновенное   значение   тока   

 

Аналогичным образом осуществляется преобразование электрических цепей, содержащих комплексные сопротивления. Комплексные сопротивления, соединенные звездой преобразуются в треугольник путем замены в формулах (2.6)—(2.9) параметров Rи G на соответствующие комплексы Zи Y. Точно также осуществляется обратное преобразование треугольник-звезда.

Например, с учетом уравнений (1.9) и (1.12) можно получить формулы преобразования «звезда—треугольник» индуктивных и емкостных элементов. Так, для емкостных элементов при преобразовании «треугольник—звезда» имеем: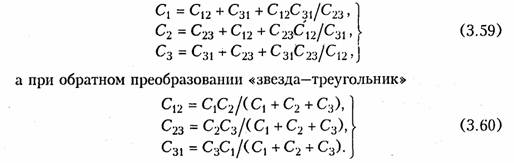



Преобразование «треугольник—звезда» и обратно для индуктивных элементов осуществляется по формулам, аналогичным (2.6)-(2.8).

Подобным же образом преобразуются матрично-топологические уравнения цепей в комплексную форму. Например, матричные уравнения (1.18), (1.20), (2.17) в комплексной форме принимают следующий вид:



где Y_B, Y_y — матрицы комплексной проводимости ветвей и комплексной узловой проводимости.

Z_B, Z_K — матрица комплексного сопротивления ветви и матрица комплексного контурного сопротивления.

Uгв, JГB, Uв — матрицы-столбцы комплексных задающих напряжений и токов ветви и напряжений ветвей.

2.7. Электрические цепи с индуктивными связями

    

В предыдущих параграфах этой главы рассматривались цепи без учета явления взаимной индукции. В то же время, при протекании тока i₁в катушке индуктивности с параметром L₁в окружающем пространстве согласно закону электромагнитной индукции создается магнитный поток Ф₁₁ (рис. 3.17, а).Если какая-либо часть этого потока Ф₁₂ пронизывает витки другой катушки с L₂,то в последней наводится ЭДС взаимной индукции, определяемая законом Максвелла —Фарадея:



где коэффициент М\2носит название взаимной индуктивностикатушек L₁и L₂.Единица измерения взаимной индуктивности — Мгенри (Гн).

Знак «—» в уравнении (3.66) определяется согласно правилу Ленцанаправлением индукционного тока, который имеет такую ориентацию, чтобы создаваемый им магнитный поток препятствовал тому изменению магнитного потока Ф₁₂, которое этот ток вызывает. Напряжение взаимоиндукции на зажимах катушки индуктивности L2: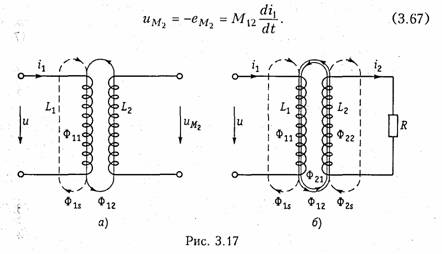



Если напряжение иприложено к катушке индуктивности Li,то под действием тока i₂в катушке L₁также будет наведена ЭДС взаимной индукции:



В соответствии с принципом взаимности (см. § 1.7) для линейных цепей М₁₂= М_21.

Рассмотренная ниже индуктивная связь носит односторонний характер: ток i₁ вызывает ЭДС взаимоиндукции ем_2, или ток i₂ — ЭДС ем_1.В случае замыкания катушки L₂на конечное сопротивление R(рис. 3.17, б) в последней под воздействием um₂ потечет индукционный ток i₂,который в свою очередь, вызовет в первой катушке L₁ЭДС взаимоиндукции ем₁(3.68). Таким образом, установится двухсторонняя индуктивная связь катушек L₁и L₂.При этом каждая из катушек L₁и L₂будет пронизываться двумя магнитными потоками: самоиндукции, вызванным собственным током, и взаимоиндукции, вызванным током другой катушки. Следовательно, в катушке L ₁индуцируется ЭДС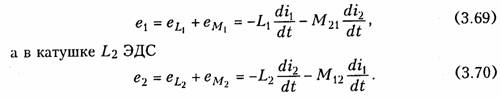



Взаимное направление потоков само- и взаимоиндукции зависит как от направления токов в катушках, так и от их взаимного расположения.

Если катушки включаются таким образом, что потоки само- и взаимоиндукции складываются, то такое включение называется согласным.Если же потоки само- и взаимоиндукции вычитаются, то такое включение принято называть встречным.На рис. 3.17, б показан случай согласного включения.

Степень связи между L\и Z-2 оценивается коэффициентом связи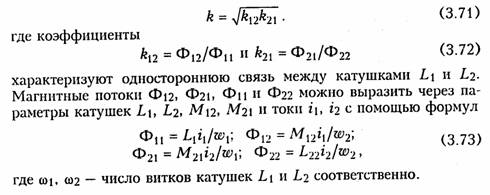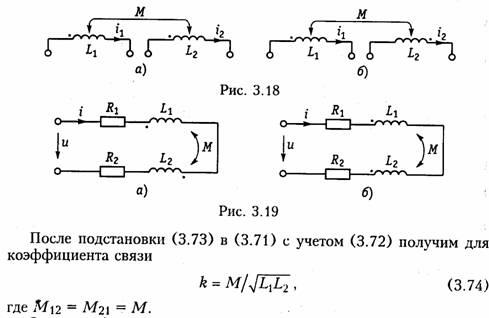





Значение kизменяется в пределах от 0 (отсутствие связи) до 1 (жесткаяили полная связь). Индуктивная связь существенным образом зависит от потоков рассеянияФ_1s и Ф_2s, поэтому степень связи иногда характеризуют коэффициентом рассеяния σ² = 1 — k².Для компактности и удобства изображения схем электрических цепей с взаимной индуктивностью вводят понятиеодноименных зажимов.Последними принято называть узлы, относительно которых одинаково ориентированные токи создают складывающиеся потоки само- и взаимоиндукции. На рис. 3.18 схематично изображены одноименные зажимы для случая согласного и встречного включений катушек L₁и L_2.Следовательно, для определения вида включения L₁и L₂на схеме достаточно определить, как ориентированы токи i₁и i₂относительно одноименных зажимов (на рис. 3.18 обозначены точкой): при одинаковой ориентации имеем согласное (рис. 3.18, а),а при разной — встречное включение (рис. 3.18, б),

Учет взаимной индуктивности существенно влияет на результаты анализа электрических цепей. Рассмотрим последовательное и параллельное соединение индуктивно-связанных катушек с индуктивностями L₁и L₂и потерями R₁и R₂, находящихся под действием гармонического напряжения: