ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 8 из 15

ARC-цепь второго порядка.На рис. 3.37 изображена активная RС-цепь (ARC-цепь) второго порядка, которая находит широкое применение в качестве типового звена различных устройств: фильтров, корректоров и др. (см.гл.14, 17, 18).

Приняв потенциал узла V₅= 0 (базисный узел) составим для узлов 3и 4уравнения по методу узловых потенциалов (рис. 3.37, б):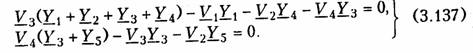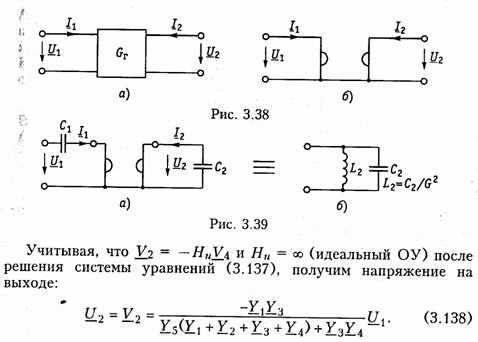





Гиратор. Гираторомназывают необратимый четырехполюник (рис. 3.38, а), описываемый уравнениями где G_r проводимость гиратора.

Условное изображение гиратора показано на рис. 3.38, б.Нагрузим гиратор сопротивлением нагрузки Z₂.Входное сопротивление гиратора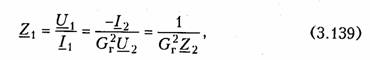



т. е. обратно сопротивлению нагрузки, поэтому гиратор часто называют инвертором положительного сопротивления.Свойство (3.139) является очень важным, поскольку позволяет имитировать индуктивность с помощью емкости. Действительно, если

 — эквивалентная индуктивность. Это свойство гираторов является очень ценным для микроэлектроники, поскольку изготовление индуктивностей по интегральной технологии представляет сложную задачу. Использование же гираторов с малым значением G_r позволяет из небольших емкостей С моделировать большие значения индуктивности L.

Существуют и другие многочисленные применения гиратора: преобразование напряжения и тока, моделирование Т- и П- образных звеньев с катушками индуктивности, трансформаторов, резонансных контуров. В качестве примера на рис. 3.39 изображена Модель параллельного колебательного контура (рис. 3.39, б) на базе гиратора (3.39, а).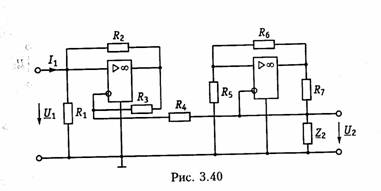



Важным свойством гиратора является то, что он не вносит энергии в цепь и не потребляет ее из цепи, т. е. ведет себя как пассивный элемент без потерь. Это следует непосредственно из уравнений

гиратора.

Реализация гиратора осуществляется с использованием активных элементов. Например, ОУ (на базе двух источников ИТУН: на базе ИТУН и ООС; на основе двух ПОС и др.). На рис. 3.40 изображена схема гиратора с двумя ИТУН, выполненными на базе ОУ.

3.1. Комплексные передаточные функции линейных

электрических цепей

Важнейшей характеристикой линейной электрической цепи является комплексная передаточная функцияH(jω). При этом электрическую цепь удобно изображать в виде четырехполюсника (рис. 4.1), на входные зажимы (1 — 1’) которого подается сигнал в виде напряжения с комплексной амплитудой Uт₁,или тока с комплексной амплитудой I_m1, а реакция снимается с выходных зажимов (2 — 2') также в виде напряжения или тока с комплексными амплитудами U_m2,I_m2.Комплексная передаточная функция (КПФ) определяется как отношение комплексной амплитуды реакции цепи к комплексной амплитуде входного воздействия.

В зависимости от типов входного воздействия и реакции цепи различают следующие виды КПФ:

1. Комплексная передаточная функция по напряжению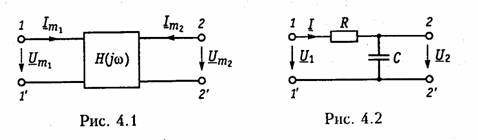





 

Комплексные передаточные функции определяются на частоте со сигнала воздействия и зависят только от параметров цепи.

Как всякую комплексную величину H(jω)можно представить в показательной, тригонометрической и алгебраической форме:



есть   вещественная   и   мнимая   части   комплексной   передаточной функции цепи.

Из (4.5) —(4.8) нетрудно получить соотношения, связывающие АЧХ и ФЧХ с вещественными и мнимыми частями комплексной передаточной функции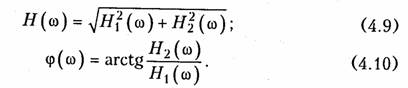





АЧХ и ФЧХ являются наиболее фундаментальными понятиями теории цепей и широко используются на практике. Важность этих характеристик для систем электрической связи, радиовещания и телевидения объясняется самой природой передачи сигналов определенного спектрального состава по каналам связи. Требования к АЧХ и ФЧХ различных устройств являются определяющими при проектировании любой аппаратуры связи, так как от степени их выполнения во многом зависит качество передачи информации.

Пример.Определить КПФ по напряжению H_u(jω), АЧХ и ФЧХ цепи, изображенной на рис. 4.2. Согласно (4.1) запишем: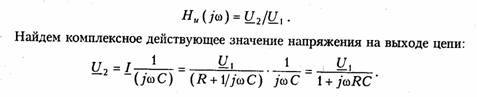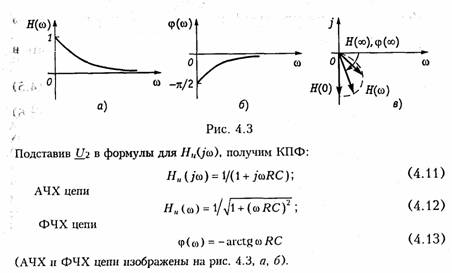





АЧХ и ФЧХ цепи можно представить единым графиком, если построить зависимость КПФ H(jω) от частоты со на комплексной плоскости. При этом конец вектора H(jω)  опишет некоторую кривую, которая называется годографомкомплексной передаточной функции (рис. 4.3, в).

В ряде случаев частотные характеристики цепи могут изменяться в очень широких пределах, поэтому более удобно их оценивать в логарифмическом масштабе. С этой целью для оценки АЧХ вводят понятие логарифмической амплитудно-частотной характеристики(ЛАХ):



Оценивается ЛАХ согласно (4.14) в децибелах (дБ). В активных цепях Кназывают еще логарифмическим усилением.Для пассивных цепей вместо коэффициента усиления оперируютослаблением цепи: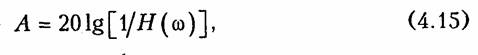



которое также оценивается в децибелах.

Наряду с передаточными функциями (4.1) —(4.4) в ряде случаев (см. гл. 16, 17,18) находят применение комплексные функции, определяющиеся отношением комплексной реакции к комплексному воздействию на входных зажимах электрической цепи (рис. 4.4)



Функции вида (4.16) носят название комплексных входных функций цепей.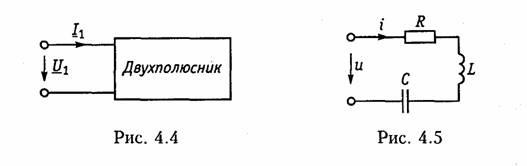



3.2. Частотные характеристики последовательного колебательного контура

В радиотехнике и электросвязи большое значение имеет явление резонанса. Резонансомназывают такое состояние электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и приложенным напряжением равен нулю. Цепи, в которых возникает явление резонанса, называют колебательными контурами,или резонансными цепями.

Колебательные контуры и явления резонанса находят широкое применение в радиотехнике и электросвязи. Резонансные цепи являются составной частью многих радиотехнических устройств: избирательные цепи в радиоприемниках и усилителях, частотно-зависимые элементы автогенераторов, фильтров, корректоров, других устройств. Для получения высоких технико-экономических показателей (избирательности, полосы пропускания, коэффициента прямоугольности, равномерности и т. д.) резонансные цепи должны иметь достаточно сложную структуру (многоконтурные связанные цепи, активные резонансные системы и др.). Некоторые из этих систем будут рассмотрены в гл. 15, 17. В настоящей главе изучим основные особенности работы цепей в режиме резонанса на примере простейших колебательных контуров.

Простейший колебательный контур содержит индуктивный и емкостный элементы, соединенные последовательно {последовательный контур)или параллельно (.параллельный контур).В последнее время широкое распространение получили резонансные цепи на базе операционных усилителей (ОУ). Различают два типа резонансов: напряжений и токов. В последовательном контуре возникает резонанс напряжений,а в параллельном — резонанс токов.

Частоту, на которой наблюдается явление резонанса, называют резонансной.

На рис. 4.5 изображена схема последовательного контура с реактивными элементами Lи Си резистивным сопротивлением R,характеризующим потери в контуре. Приложим к контуру гармоническое напряжение  с частотой ω.   Комплексное  входное сопротивление контура на данной частоте определяется согласно уравнению



На резонансной частоте комплексное сопротивление носит чисто активный характер, т. е. Z = R,ток совпадает по фазе с приложенным напряжением и достигает максимального значенияIо =  U/R.Реактивные сопротивления контура на резонансной частоте ω₀ равны друг другу:



Величина ρ носит название характеристического сопротивленияконтура.

Резонансные свойства контура характеризуются добротностью контура,которая в общем случае определяется величиной



где W_p— максимальные значения реактивной энергии, запасенной в контуре при резонансе; W_T—активная энергия, поглощаемая в контуре за период Т.Величина, обратная добротности, называется затуханием контураи обозначается d:



Величина Qбезразмерна и обычно колеблется для реальных контуров от 10 до 100 и выше. Для выяснения физического смысла параметра Qисследуем энергетические соотношения в контуре при резонансе. Положим, например, что при резонансе ток в цепи 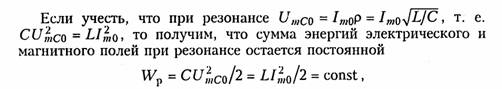Определим согласно (1.10) и (1.13) сумму энергий электрического и магнитного полей:





так как уменьшение WLсопровождается увеличением Weи наоборот. Таким образом,

происходит периодический обмен энергией между элементами I и С без участия источника. Энергия источника расходуется только на покрытие тепловых потерь в элементе активного сопротивления R;реактивная мощность при резонансе не потребляется.

Активная энергия, рассеиваемая в контуре за период Т,равна



Таким образом, добротность Q показывает, во сколько раз резонансные напряжения на реактивных элементах превышают приложенное напряжение. Отсюда следует и термин «резонанс напряжений». Это свойство контура «усиливать» приложенное напряжение резонансной частоты широко используется на практике.

Величины ρ,  ω_о,  Q, dявляются вторичными параметрамиконтура в отличие от величин R, L, Сназываемых первичными.

Анализируя характер уравнений напряжений и токов в RLC-цепи, фазовых сдвигов между ними при гармоническом воздействии нетрудно видеть, что они являются частотно-зависимыми. Эта зависимость вытекает непосредственно из зависимости реактивных   элементов  XLИ  ХС .ОТ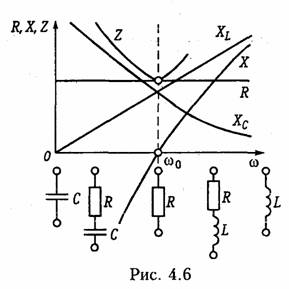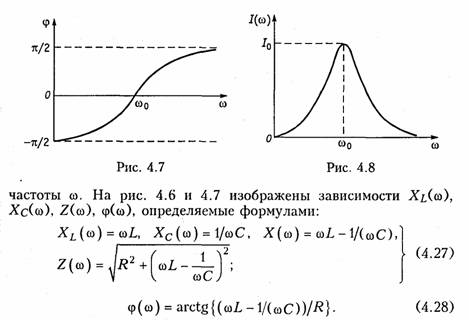         





 

Из представленных характеристик следует, что при ω <ω₀ цепь имеет емкостный характер (Х<0; φ <0)И ТОК опережает по фазе приложенное напряжение при ω >ω₀ характер цепи индуктивный (X > 0; φ > 0) и ток отстает по фазе от приложенного напряжения; при со = соо наступает резонанс напряжений (X=0; φ = 0) и ток совпадает по фазе с приложенным напряжением. Полное сопротивление цепи принимает при этом минимальное значение Z=R.

Зависимость действующего значения тока от частоты можно найти из уравнения (4.18)*:



Зависимости I(ω), UL(ω), U_C(ω) называются резонансными характеристиками токаи напряжений.Анализ зависимости I(ω) показывает, что она достигает максимума при резонансе ω =ω₀



Выходное напряжение обычно снимается с емкостного или индуктивного элемента контура. В соответствии с этим представляет наибольший практический интерес КПФ по напряжению относительно элементов С и L: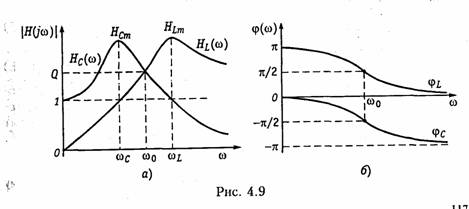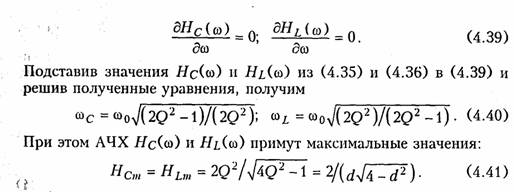









Анализ полученных зависимостей показывает, что с увеличением добротности Q(уменьшением затухания d)частоты ωс и ω_L сближаются с резонансной частотой ω_о.При этом C_Cти H_Lmвозрастают.

Степень отклонения режима колебательного контура от резонанса принято оценивать абсолютной, относительнойи обобщенной расстройками. Отклонение от резонансного режима может происходить в результате изменения частоты; задающего генератораили вариации параметров контура.                                       

Расстройки определяются следующим образом:

абсолютная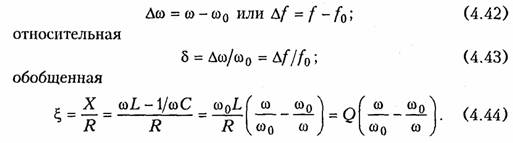     

                                                                                \

Наиболее широко в теоретических исследованиях применяется обобщенная расстройка ζ,так как ее использование существенно упрощает расчет. Например, модуль входной проводимости можно записать через обобщенную расстройку ζ, в форме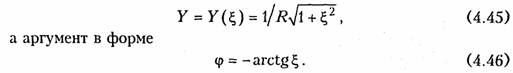



Важной характеристикой колебательного контура является полоса пропускания. В общем случае абсолютной полосой пропусканияназывают диапазон частот в пределах которого коэффициент передачи уменьшается в √2 раз по сравнению с максимальным*. Абсолютная полоса пропускания равна



Уравнения (4.50) могут быть положены в основу экспериментального определения добротности по резонансной кривой тока I(ω). Формула (4.50) показывает, что чем выше добротность Q, тем меньше полоса пропускания и наоборот. Причем, поскольку с увеличением потерь Rдобротность контура падает, то подключение к контуру сопротивления нагрузки или источника с внутренним сопротивлением приводит к расширению полосы пропускания.