ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 11 из 15

Параметры типовых четырехполюсников.К типовым пассивным четырехполюсникам относят Г-, Т-, П- образные схемы (см. рис. 12.2, б —г),мостовые (см. рис. 12.2, а)и Т- перекрытые схемы (см. рис. 12.2, д).Можно получить, основываясь на матричных методах расчета, параметры типовых четырехполюсников, если рассматривать их как сложные четырехполюсники, состоящие из соединений простейших четырехполюсников.

Рассмотрим сначала простейшие четырехполюсники, изображенные на рис. 12.8, аи 6.Для первого из них (рис. 12.8, а),пользуясь законами Кирхгофа, можно записать: 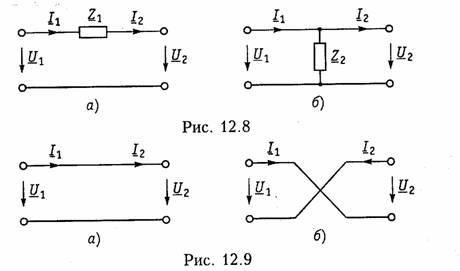и



I₁=I_2.Сравнивая эти уравнения с уравнениями в А-параметрах (12.4), можно записать матрицу А для такого четырехполюсника: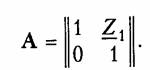



Для второго простейшего четырехполюсника (рис. 12.8, б)имеем 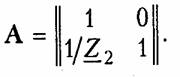 и поэтому



Другие матрицы — Z,YиН — могут быть легко получены из табл. 12.1. Заметим, что для первого простейшего четырехполюсника не существует Z-параметров, так как все они обращаются в бесконечность. По этой же причине для второго простейшего четырехполюсника не существует Y-параметров.

На рис. 12.9, а, бпоказаны соответственно прямое и скрещенное соединения. Нетрудно убедиться, что прямому соединению соответствует матрица



Найдем теперь параметры типовых пассивных четырехполюсников, изображенных на рис. 12.2. Г- образный четырехполюсник (рис. 12.2, б)получается путем каскадного соединения простейших четырехполюсников, приведенных на рис. 12.8, а и б. Его матрица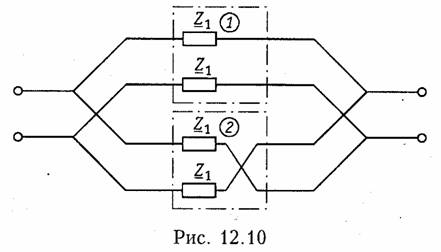



А может быть получена перемножением вышеприведенных матриц простейших четырехполюсников: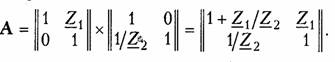



Для Т- образного четырехполюсника (рис. 12.2, в)матрицу Aможно найти, если рассматривать его как каскадное соединение Г образной схемы с элементами Z₁, и Z₂ и простейшей схемы с элементом Z₃ в продольном плече (рис. 12.8, а):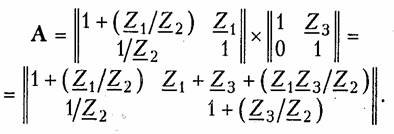



Для П- образной схемы (рис. 12.2, г),если ее представить в виде каскадного соединения простейшего четырехполюсника, изображенного на рис. 12.8, б и Г- образного четырехполюсника с элементами Z₂ в продольном плече и Z₃в поперечном плече, матрица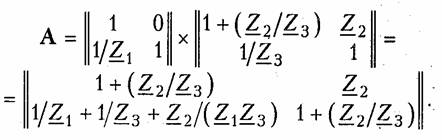



Зная А-параметры Г-, Т- и П- образных четырехполюсников, можно найти по табл. 12.1 другие системы параметров-коэффициентов.

Мостовой четырехполюсник (см. рис. 12.2, а)можно представить как параллельное соединение двух простейших четырехполюсников (рис. 12.10). При параллельном соединении следует пользоваться матрицами Y. Используя данные табл. 12.1, найдем по известным матрицам А простейших четырехполюсников (второй из них имеет скрещенные выходные зажимы) их матрицы Yи, просуммировав последние, получим результирующую матрицу Y мостового четырехполюсника. Матрицы Y простейших четырехполюсников с учетом скрещивания выходных зажимов во втором равны



Предлагаем читателям самостоятельно найти параметры Т- перекрытого четырехполюсника (см. рис. 12.2, Э), рассматривая его как параллельное соединение простейшего четырехполюсника с сопротивлением Z₄ в продольном плече и Т- образного четырехполюсника.

Параметры зависимых источников.Системе уравнений в Y- naраметрах (12.2, б) можно сопоставить в соответствии с ЗТК схему с двумя зависимыми источниками типа ИТУН (рис. 12.11, а).Если положить 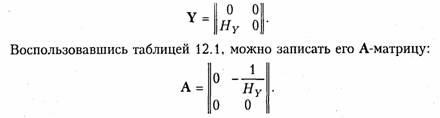то получим идеальный источник тока, управляемый напряжением (рис. 1.7, б). Таким образом, Y-матрица идеального ИТУНа равна



Аналогичным образом системе уравнений (12.5) в Н-параметрах можно сопоставить согласно ЗНК схему с двумя зависимыми

источниками: ИНУН и ИТУН (рис. 12.11, б). Принимая

   переходим к идеальному источнику тока, управляемому током (рис. 1.7, г).Его матрица Н имеет вид





Она может быть представлена схемой, показанной на рис. 12.11, г.При данная схема превращается в идеальный ИНУН (рис. 1.7, а).Следовательно,F-матрица ИНУН записывается в виде:



К числу простейших активных линейных четырехполюсников с зависимыми источниками относятся транзисторы и лампы, работающие в линейном режиме.

Чаще всего для транзисторов используют уравнения передачи в Н- или Y-параметрах. Иногда используются также Z-параметры. Усредненные значения Y-,Z- и Н-параметров транзисторов приводятся в справочной литературе. Следует иметь в виду, что одни и те же параметры имеют различные значения в зависимости от того, какой именно из электродов транзистора (эмиттер, база, коллектор) является общим для входной и выходной пар зажимов транзистора как четырехполюсника. Различают поэтому Y-,Z- и Н-параметры транзисторов с общим эмиттером, с общей базой и с общим коллектором.

Пример.Определим параметры биполярного транзистора п-р-птипа, включенного по схеме с общим эмиттером (рис. 12.12, я). Его схема замещения в области нижних частот показана на рис. 12.12, б.Сравнивая эту схему со схемой рис. 12.11, а,видим, что при  обе схемы становятся идентичными. Следовательно, Y-матрица биполярного транзистора с общим эмиттером имеет вид



Электронная лампа как четырехполюсник чаще всего характеризуется Y- или А-параметрами. Для электронной лампы с общим катодом, если считать, что сеточные токи отсутствуют, и не учитывать паразитные емкости, имеем:



где S— крутизна электронной лампы (скорость изменения анодного тока с изменением сеточного напряжения); R_i— внутреннее сопротивление лампы; μ — коэффициент усиления лампы (см. §1.2).

При перечисленных выше условиях Z- и Н-параметров для электронной лампы не существует. В общем случае, когда с влиянием между электродами лампы через паразитные элементы приходится считаться, ни один из параметров лампы с учетом ее паразитных элементов не равен нулю и лампа как четырехполюсник может характеризоваться любой системой параметров.

Параметры сложных четырехполюсников.При анализе сложного четырехполюсника следует выделить простейшие и типовые четырехполюсники и установить способы их соединения. Затем с помощью матричных методов расчета можно определить соответствующие матрицы сложного четырехполюсника.

Пример.Рассмотрим методику определения Н-параметров каскада усилителя на транзисторе со схемой, показанной на рис. 12.13, а. Каскад усилителя образуется в результате параллельного соединения транзистора и П- образного пассивного четырехполюсника (рис. 12.13, б).Поэтому следует оперировать матрицами Yсоединяемых четырехполюсников. Ранее для П- образной схемы была найдена матрица А. От нее с помощью табл. 12.1 можно перейти к матрице Y П- образного четырехполюсника. Для транзистора, включенного по схеме с общим эмиттером, Y-параметры определяем из выбранной модели (рис. 12.13, в), либо берем из справочника. Просуммировав найденные таким образом матрицы YП- образного четырехполюсника и транзистора, получим матрицу Y усилительного каскада. Далее по табл. 12.1 перейдем к искомой матрице Н усилительного каскада.

 

4.4. Параметры холостого хода и короткого

замыкания четырехполюсника

 

Входное сопротивление четырехполюсника.Если к одной паре зажимов четырехполюсника, например 2 — 2',подключить произвольное сопротивление Z_H (рис. 12.14, а),то со стороны другой пары зажимов, т. е. 1 — 1',четырехполюсник можно рассматривать как двухполюсник с входным сопротивлением Z_BX1, которое называют входным сопротивлением четырехполюсника. Следовательно,

Входное сопротивление можно выразить через параметры четырехполюсника. Проще всего это сделать, воспользовавшись выражениями для U₁, и I₁ из уравнений передачи в А-параметрах (12.4). В этом случае



В связи с тем, что изменилось направление передачи энергии, следует воспользоваться уравнениями передачи (12.6). Тогда



Заметим, что при изменении направления передачи энергии через четырехполюсник в выражениях (12.11) и (12.12) параметры A₁₁, и A₂₂ поменялись местами (см. свойство 4, § 12.2).

Входное сопротивление четырехполюсника не является его внутренним параметром, так как оно зависит не только от свойств четырехполюсника, но и от свойств внешней цепи (нагрузки), на которую замкнута пара зажимов четырехполюсника.

Параметры холостого хода и короткого замыкания.Формулы (12.11) и (12.12) описывают входные сопротивления четырехполюсника при произвольных сопротивлениях нагрузки Z_Hи Z_r. Из них легко получить значения Z_BX1 и Z_BX2при разомкнутых и замкнутых накоротко зажимах четырехполюсника.

В режиме холостого хода на зажимах 2—2'(выходные зажимы разомкнуты) входное сопротивление четырехполюсника со стороны зажимов 1 — 1' обозначается Z_xx1 и определяется из формулы (12.11) при Z_H = ∞:



Величины  называются параметрами холостого ходаи короткого замыкания.Значения этих параметров для любой данной частоты могут быть измерены с помощью специального прибора для измерения комплексных сопротивлений — моста переменного тока. Это особенно удобно, когда четырехполюсник представляется в виде «черного ящика» и нет возможности узнать его содержимое или рассчитать какие-либо другие системы параметров, либо когда влияние паразитных элементов четырехполюсника трудно учесть аналитически. Измерение же других систем параметров часто представляет значительную сложность.

Из приведенных выше соотношений для параметров XX и КЗ легко получить, что  т.е. только три параметра из четырех являются независимыми. Этих параметров достаточно для составления уравнений передачи пассивного четырехполюсника, причем из параметров XX и КЗ может быть получена любая система параметров-коэффициентов.

У активного четырехполюсника все четыре параметра независимы, поэтому их нельзя найти по параметрам XX и КЗ.

В случае симметричного пассивного четырехполюсника параметры  симметричный четырехполюсник характеризуется только двумя параметрами XX и КЗ.

 

4.5. Характеристические параметры четырехполюсника

 

Согласованное включение четырехполюсника.При передаче сигналов на расстояние может участвовать большое число каскадно соединенных четырехполюсников. На практике используется такое включение четырехполюсников, которое получило название согласованного.Если рассматривать четырехполюсник, включенный по схеме рис. 12.1, то это означает, что должны выполняться два условия: т. е. входное сопротивление четырехполюсника должно быть согласовано с сопротивлением генератора, а выходное — с сопротивлением нагрузки.

В случае каскадного включения нескольких четырехполюсников обеспечивают согласованное включение каждого из них.

Режим согласованного включения является наиболее благоприятным при передаче сигналов, поскольку при этом отсутствуют отражения электрической энергии (а значит, ее рассеяние) на стыках «генератор —четырехполюсник» и «четырехполюсник —нагрузка» и искажение сигнала.

Характеристические сопротивления четырехполюсника.Остается не ясным, всегда ли можно включить четырехполюсник согласованно, т. е. всегда ли можно подобрать такие сопротивления Z_r и Z_H, при которых



Оказывается, для любого четырехполюсника всегда существует такая пара сопротивлений, для которой выполняется условие (12.16). Эти сопротивления называютсяхарактеристическими(собственными) сопротивлениями четырехполюсника и обозначаются Z_c1 и Z_с2. Индекс «1» указывает на то, что характеристическое сопротивление определяется со стороны зажимов 1 — 1',а индекс «2» — со стороны зажимов 2—2'.



Таким образом, если в качестве внутреннего сопротивления генератора выбрать  качестве сопротивления нагрузки  Рисунок 12.15 иллюстрирует это свойство характеристических сопротивлений.

Можно теперь уточнить определение режима согласованного включения. Режимом согласованного включения четырехполюсниканазывается такой режим его работы, когда внутреннее сопротивление генератора выбрано равным характеристическому сопротивлению четырехполюсника Z_c1, а сопротивление нагрузки равным характеристическому сопротивлению Z_C2.



Совместное решение этих уравнений относительно величин Z_с1, и Z_с2  дает выражение характеристических сопротивлений через А-параметры:



Характеристическое сопротивление можно выразить через параметры XX и КЗ. Проще всего это получить из (12.17), если воспользоваться формулами (12.13) — (12.15), где параметры XXи КЗ выражены через А-параметры:



Последние формулы удобны для экспериментального определения характеристических сопротивлений методами XX и КЗ.