ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 12 из 15

Пример.Дан резистивный Г- образный четырехполюсник (см. рис. 12.2, б) с элементами Z₁= 1600 Ом, Z₂=900 Ом. Включим его согласованно с генератором и нагрузкой. Для согласования четырехполюсника с генератором нужно выбрать его внутреннее сопротивление равным характеристическому сопротивлению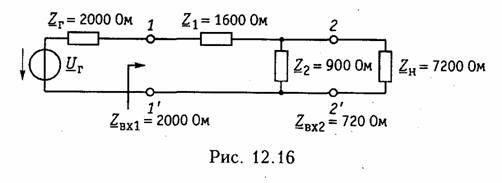



четырехполюсника со стороны зажимов 1 —1', т. е. Z_r = Z_c1. Чтобы согласовать четырехполюсник с нагрузкой, следует подключить к его зажимам 2—2'сопротивление нагрузки Z_H = Z_C2.

Матрица А четырехполюсника имеет вид



Характеристическая постоянная передачи четырехполюсника.

При согласованном включении на стыках «генератор —четырехполюсник» и «четырехполюсник —нагрузка» рассеяние электрической энергии будет происходить только в четырехполюснике (например, она будет превращаться в тепловую энергию на резистивных элементах схемы).

Чтобы учесть эти потери, вводят меру передачи энергии — характеристическую (собственную) постоянную передачи четырехполюсника,определяемую через отношение произведения напряжения и тока на входе четырехполюсника к произведению напряжения и тока на его выходе, взятое-в логарифмическом масштабе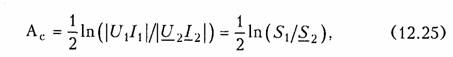







где S₁и S₂ — полные мощности на входе и выходе четырехполюсника при согласованном его включении, называется характеристическим (собственным) ослаблением четырехполюсника.Она показывает в логарифмическом масштабе, на сколько уменьшилась мощность на выходе четырехполюсника по сравнению с мощностью на его входе при передаче энергии через четырехполюсник в режиме согласованного включения.

Для симметричного четырехполюсника из (12.21) получаем





Бел достаточно крупная единица измерения. Вместо нее обычно применяют в 10 раз меньшую единицу — децибел(сокращенно дБ). Поскольку 1 Б = 10 дБ, то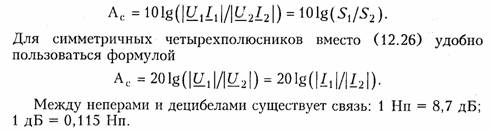



Пример. Несимметричный и симметричный четырехполюсники включены согласованно. Мощность на выходе первого из них уменьшается по сравнению с мощностью на входе в 1000 раз, на выходе второго по сравнению с его входом — в 10 000 раз. Определим характеристические (собственные) ослабления четырехполюсников.

Характеристическое ослабление по мощности для несимметричного четырехполюсника согласно формуле (12.25) составляет Ас = 10 lg 1000 = 30 дБ, а для симметричного - А_с = 10 lg 10 000 = 40 дБ. Кроме того, для симметричного четырехполюсника можно указать характеристическое ослабление по напряжению и току. В соответствии с (12.25) оно равно 20 lg 10 000 = 80 дБ.

Второе слагаемое в формуле (12.24)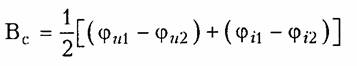



учитывает изменение начальных фаз напряжений и токов при передаче энергии через согласованно включенный четырехполюсник и носит название характеристической (собственной) фазыили фазовой постоянной четырехполюсника.

Преобразование (12.21) для симметричного четырехполюсника приводит к характеристической (собственной) фазовой постоянной, равной разности фаз входного и выходного напряжений или токов:



Измеряется фазовая постоянная в радианах(сокращенно рад) или градусах(сокращенно град).

Величины Zc₁, Zc₂ и Г_с образуют систему характеристических {собственных) параметров четырехполюсника.Она полностью описывает пассивный четырехполюсник.

Связь с другими системами параметров.Вычисление характеристических параметров по А-параметрам осуществляется с помощью формул (12.17), (12.22), а по параметрам XX и КЗ — с помощью формул (12.18) и (12.23). Установим обратные соотношения, т. е. выразим А-параметры и параметры XX и КЗ через характеристическое.

Из (12.22) следует:





 

Заметим, что из этих формул легко выводится формула (12.23), приведенная ранее без вывода.

Расчет каскадного согласованного соединения четырехполюсников.При расчете каскадного соединения четырехполюсников ранее был использован матричный метод, в котором матрица А результирующего четырехполюсника определялась произведением матриц А составляющих четырехполюсников. Если четырехполюсники соединены согласованно, то удобнее пользоваться характеристическими параметрами.

На рис. 12.17 показано каскадное согласованное включение трех четырехполюсников с характеристическими постоянными передачи Г_с1, Г_С2 и Гс_З.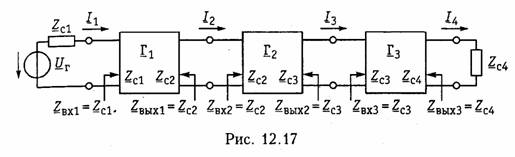



Согласование четырехполюсников состоит в том, что характеристические сопротивления со стороны их соединения выбраны равными друг другу, а внутреннее сопротивление генератора и сопротивление нагрузки — равными характеристическим сопротивлениям крайних четырехполюсников. Действительно, крайний справа четырехполюсник нагружен на сопротивление, равное его характеристическому Z_с4, значит, входное сопротивление этого крайнего четырехполюсника будет равно характеристическому сопротивлению Zc₃предшествующего четырехполюсника. В свою очередь, входное сопротивление среднего четырехполюсника оказывается равным характеристическому сопротивлению Zc₂ крайнего левого четырехполюсника. Следовательно, входное сопротивление крайнего слева четырехполюсника равно Zc₁и согласовано с внутренним сопротивлением генератора.

Аналогичным образом можно провести рассуждения, начиная с левого четырехполюсника.

На рис. 12.17 во избежание путаницы входные сопротивления четырехполюсников со стороны зажимов 2—2'названы выходными сопротивлениями четырехполюсников. Определим характеристическую постоянную передачи результирующего четырехполюсника. Согласно (12.20)



Таким образом, результирующий четырехполюсник, составленный из каскадно и согласованно соединенных отдельных четырехполюсников, имеет характеристические сопротивления, равные характеристическим сопротивлениям крайних четырехполюсников, и оказывается включенным согласованно с генератором и нагрузкой. Его характеристическая постоянная передачи равна сумме характеристических постоянных передачи соединяемых четырехполюсников. Учитывая, что Г_с = А_с + jВ_с, можно записать:

5.1. Классификация фильтров

 

Электрический фильтр — это устройство, которое практически не ослабляет спектральные составляющие сигнала в заданной полосе частот и значительно ослабляет (подавляет) все спектральные составляющие вне этой полосы.

Полоса частот, в которой ослабление мало, называется полосой пропускания.Полоса частот, в которой ослабление велико, называется полосой непропускания (задерживания).Между этими полосами находится переходная область.

По расположению полосы пропускания на шкале частот различают следующие фильтры:

нижних частот (ФНЧ), в которых полоса пропускания располагается на шкале частот от ω = 0 до некоторой граничной частоты ω = ω _п, а полоса непропускания (задерживания) — от частоты ω = ω₃ до бесконечно больших частот (рис. 17.1,а);

верхних частот (ФВЧ) с полосой пропускания от частоты ω = ω_п до бесконечно больших частот и полосой непропускания от частоты  ω= 0 до ω= ω_з (рис. 17.1, б);

полосовые (ПФ), в которых полоса пропускания ω_п1...ω_п2 располагается между полосами непропускания О...ω₃₁ и ω₃₂...∞ (рис. 17.1, в);

заграждающие (режекторные) (ЗФ или РФ), в которых между полосами пропускания О...ω_п1 и ω_П2…∞ находится полоса непропускания ω₃₁...ω₃₂ (рис. 17.1, г);



многополосные, имеющие несколько полос пропускания.

На рис. 17.1, а — гпоказаны также условные обозначения фильтров каждого типа в соответствии с ГОСТ.

В соответствии с используемой элементной базой к настоящему моменту выделились несколько классов фильтров. Исторически первыми (и все еще широко применяемыми) являются пассивные фильтры, содержащие элементы Lи С.Они носят название LC-фильтров.

Во многих случаях на практике требовалась крайне высокая избирательность (различие ослаблений в полосах пропускания и непропускания в десятки тысяч раз). Это привело к появлению фильтров с механическими резонаторами: кварцевых, магнитострикционных, электромеханических.

По-видимому, самые значительные достижения в области теории и проектирования фильтров связаны с успехами микроэлектроники. Требования микроминиатюризации радиоэлектронной аппаратуры заставили отказаться от использования индуктивностей, которые имеют большие габаритные размеры, особенно на низких частотах, и не поддаются исполнению в микроминиатюрном виде. Появились активные .RC-фильтры, состоящие из резисторов, конденсаторов и активных приборов (например, транзисторов). Эти фильтры могут быть выполнены в виде микромодульной конструкции или интегральной схемы. Применение активных .RC-фильтров ограничивается пока сравнительно небольшим диапазоном частот до десятков (иногда сотен) килогерц.

Разработка цифровых систем связи и достижения в области цифровых вычислительных машин стимулировали создание фильтров на базе элементов цифровой и вычислительной техники — цифровых фильтров. В силу специфики элементной базы цифровых фильтров не будем далее упоминать о них, хотя расчет таких фильтров производится методами теории электрических цепей. Заинтересованные читатели могут обратиться к специальной литературе по цифровым фильтрам.

В идеальном случае (идеальный фильтр) характеристика рабочего ослабления, например для ФНЧ, имеет вид, показанный на рис.  17.2, а.С рабочим ослаблением связана рабочая амплитудно-частотная характеристика (АЧХ):  На рис. 17.2, бизображена АЧХ идеального фильтра нижних частот.



Реальные фильтры (т. е. фильтры, состоящие из реальных  элементов)  имеют  характеристики рабочего ослабления и амплитудно-частотную,



 

отличные от идеальных.

Требования к электрическим характеристикам фильтров задаются в виде допустимых пределов изменения этих характеристик. Так, рабочее ослабление в полосе пропускания не должно превышать некоторого максимального допустимого значения А_{р тах},а в полосе непропускания не должно быть ниже некоторого минимально допустимого значения А_{р тix}.Нетрудно изобразить эти требования графически, как это сделано на рис. 17.3, адля ФНЧ. На этом рисунке ω_п и ω₃ — граничные частоты полос пропускания и непропускания.

Зная требования к Ар,можно пересчитать их в требования к АЧХ или, как это принято в теории фильтров, в требования к квадрату АЧХ (рис. 17.3, б):



Характеристики проектируемых фильтров должны «укладываться» в эти требования (рис. 17.3, аи б).

Помимо требований к частотной зависимости рабочего ослабления (а значит, и к АЧХ) могут задаваться также требования к фазочастотной характеристике фильтра (скажем, допустимые отклонения от линейного закона) и величине нелинейных искажений (обусловленных, например, наличием железа в катушках индуктивности). Могут предъявляться требования и к другим характеристикам и параметрам фильтра. Ниже будем учитывать только требования к рабочему ослаблению и АЧХ.

Идеальные частотные характеристики фильтра (см. рис. 17.2, а)заведомо нереализуемы. Частотные характеристики реальных фильтров могут лишь приближаться к ним с той или иной степенью точности в зависимости от сложности схемы фильтра.

 

5.2. Аппроксимация характеристик фильтров нижних частот

 

Функция фильтрации.В общем виде электрические фильтры описываются передаточной функцией вида:



могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов d_kудовлетворить заданным требования (см. рис. 17.3).

В теории фильтров принято иметь дело не с обычной угловой частотой ω, а с нормированной частотойΩ = ω/ω_н, где ω_н — нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания ω_п, так что 

В теории электрических фильтров вместо формул (17.2) и (17.3) используют другие, также универсальные для любого типа фильтра:



Функция ψ²(Ω)называется функцией фильтрации, a ε — коэффициентом неравномерности ослабления. В общем случае ψ(Ω)— это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: —1 ≤ | ψ(Ω)| ≤1 в полосе пропускания и | у (Q )| » 1 в полосе непропускания фильтра.

В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева.Если ψ(Ω)— дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева.Все эти три типа фильтров будут рассмотрены в этой главе.

Следует отметить, что имеет смысл подробно изучать только фильтры нижних частот, т. к. другие типы фильтров (верхних частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью замены переменной (частоты). Для этого во всех выражениях, содержащих переменную Ω, нужно произвести замену переменной таким образом, чтобы характеристики ФНЧА_р(Ω)и |Нp(jΩ)|² преобразовались в характеристики соответствующего фильтра. Подобная замена переменной Ω называется преобразованием частоты,а исходный ФНЧ — фильтром НЧ-прототипа.

Преобразование частоты позволяет установить соответствие между частотами полос пропускания и непропускания НЧ-прототипа и частотами фильтров верхних частот, полосового или заграждающего, а также преобразовать схему ФНЧ в схемы ФВЧ, ПФ или ЗФ. Более подробно вопросы, связанные с преобразованием частоты, будут рассматриваться в § 17.5.