ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 7 из 15

Последовательное соединение.Для согласного включения катушек (см. рис. 3.19, а)в соответствии с ЗНК и уравнениями (3.66) и (3.67) можно записать: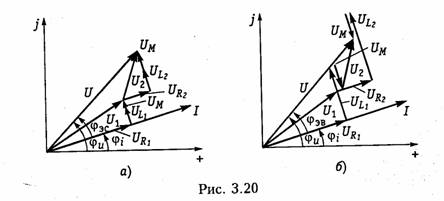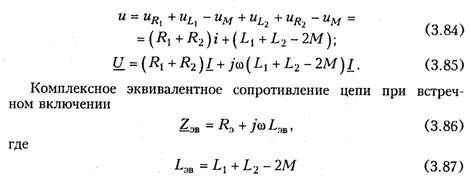







— эквивалентная индуктивность цепи при встречном включении катушек индуктивности.

Как следует из (3.78) и (3.87) эквивалентная индуктивность при согласном включении больше на 2М, а при встречном меньше на 2Мсуммарной индуктивности L₁+ L_2.

Уравнения для тока I, фазового сдвига φ_ЭB и напряжений U₁,U₂аналогичны (3.80)-(3.83):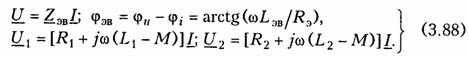



На рис. 3.20, бизображена векторно-топографическая диаграмма напряжений для случая встречного включения. При встречном включении катушек может наблюдаться «емкостный эффект», когда фазовый сдвиг между током и напряжением одной из катушек будет отрицательный. Это может иметь место при выполнении условия Li< М.В этом случае U_L2<UMИ



и напряжение U2 будет отставать от тока I. Однако вся цепь всегда будет носить индуктивный характер, так как при любых значениях параметров L₁,L₂и Мсправедливо условие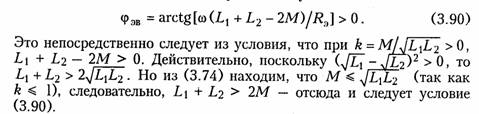



Уравнения (3.79) и (3.87) можно положить в основу экспериментального определения взаимной индуктивности М.Для этого достаточно определить ток I, напряжение U,мощность Рв цепи при согласном и встречном включениях катушек и найти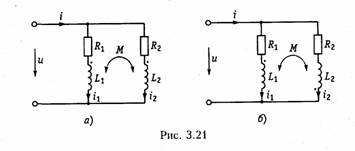





где индексы «с» и «в» относятся к согласному и встречному включениям.

Реактивные составляющие комплексных сопротивлений при согласном и встречном включениях можно определить как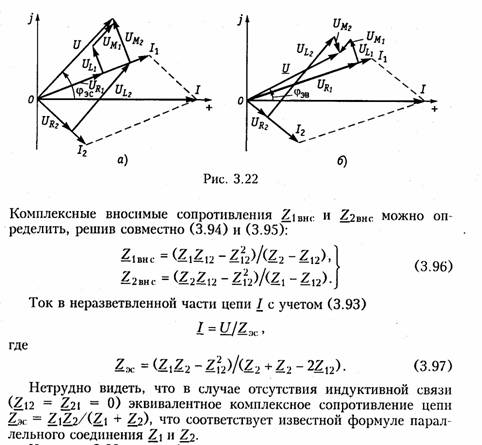





На рис. 3.22, аизображена векторно-топографическая диаграмма для случая согласного включения L₁и L_2.Аналогичным образом можно получить соответствующие уравнения для встречного включения катушек (см. рис. 3.21, б).При этом необходимо учесть, что в уравнениях перед слагаемыми с Z₁₂ и Z₂₁ необходимо заменить знак на противоположный. Так, уравнения (3.94), (3.96), (3.97) принимают вид



На рис. 3.22, 6изображена векторно-топографическая диаграмма для случая встречного включения.

Из уравнений (3.94), (3.98) нетрудно найти эквивалентные индуктивности ветвей:



где знак «—» относится к согласному, а «+» — к встречному включению индуктивно связанных элементов.

2.8 Трансформатор

Трансформаторомназывается статическое устройство, предназначенное для преобразования значений переменных напряжений и токов. Простейший трансформатор состоит из двух индуктивно связанных катушек с индуктивностями L₁и L₂,расположенных на общем сердечнике. Катушка, к которой подключается источник, называют первичной,а к которой подключают нагрузку — вторичной.Сердечник может быть выполнен из ферромагнитного или неферромагнитного материала. Примером трансформатора последнего типа является воздушный трансформатор, находящий широкое применение в технике связи, измерительных приборах, различных радиотехнических устройствах.

Воздушный      трансформатор.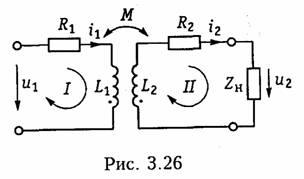



На рис. 3.26 изображена схема простейшего воздушного трансформатора с потерями в первичной R₁и вторичной R₂катушках (обмотках), нагруженного на комплексное сопротивление Z_H =R_н+jХ_н.

Составим уравнение трансформатора по ЗНК для I и II контуров:



Уравнениям (3.110) соответствуют одноконтурные схемы замещения воздушного трансформатора, изображенные на рис. 3.27. Значения величин R_1BH и X_1BH, R₂вн и Х_2ВН определяются из (3.109) с учетом (3.107):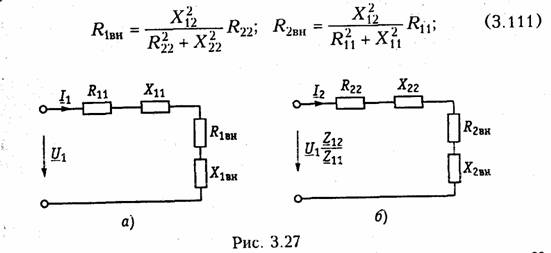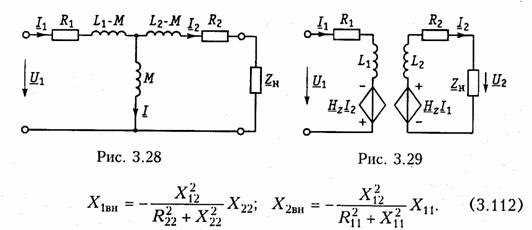



 



 

Знак «—» в уравнениях (3.112) свидетельствует о размагничивающем действии вторичной обмотки на первичную.

С физической точки зрения R_1ВНИ R_2ВН представляют собой эквивалентные резистивные сопротивления, вносимые за счет взаимной индуктивности соответственно в контуры I и II.

При этом на Rвн при протекании тока I₁рассеивается та же мощность, что и на R₂ при протекании тока I₂ и соответственно на R_2вн при протекании I₂ рассеивается та же мощность, что и на R₁при протекании I₁.

Воздушный трансформатор может быть представлен двухконтурной схемой замещения, изображенной на рис. 3.28. Эта схема получается непосредственно из схемы, изображенной на рис. 3.26 после объединения в один узел одноименных зажимов и развязки индуктивных связей согласно рис. 3.24. Таким, образом, для определения токов в воздушном трансформаторе могут быть использованы одно- либо двухконтурные эквивалентные схемы замещения.

Если в уравнениях (3.107) обозначить то воздушный трансформатор можно представить схемой замещения с зависимыми источниками (рис. 3.29).

Из общих уравнений для комплексных токов I₁ и I₂ с учетом (3.106), (3.107) можно найти отношение комплексных токов и напряжений в воздушном трансформаторе:



где k_ТР= L₁/M— коэффициент трансформации.Как видно, в данном случае отношение напряжений не зависит от нагрузки, а отношение токов зависит от Z_H. Такой трансформатор называют совершенным.Для него коэффициент связи k= 1, а коэффициент рассеяния = 0.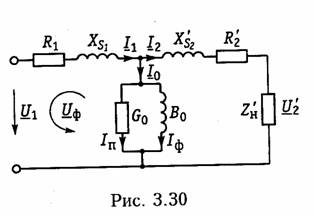    



Существует     еще     понятие идеального трансформатора,у которого потери равны нулю,индуктивности катушек бесконечно велики, а их отношение равно коэффициенту трансформации ω₂— число витков первичной и вторичной катушек. В идеальном трансформаторе отношение как токов, так и напряжений не зависит от нагрузки и определяются только коэффициентом трансформации k_тр.

Трансформатор с ферромагнитным сердечником.Ферромагнитный сердечник применяется для увеличения магнитного потока и связи между катушками, что приводит к росту мощности, отдаваемой во вторичную цепь трансформатора. При этом по своим свойствам он приближается к идеальному трансформатору, но становится в общем случае нелинейным устройством вследствие появления дополнительных потерь на гистерезис и вихревые токи. Однако на практике трансформатор с ферромагнитным сердечникомстараются конструировать таким образом, чтобы нелинейность была мала и ею можно было пренебречь. Тогда расчет подобного трансформатора можно осуществить на основе двухконтурной схемы замещения, изображенной на рис. 3.30 с параметрами, приведенными к параметрам первичной обмотки. Данная схема может быть получена по аналогии со схемой рис. 3.28 с учетом потерь в стали Go и намагничивания Во.Приведенные значения X'_S2, I'2 определяются согласно равенствам:



2.9. Баланс мощности                                

 

Представим пассивную электрическую цепь, находящуюся под воздействием источника гармонического напряжения, в форме двухполюсника (см. рис. 1.1). Под воздействием напряженияи_nb== U_msinωt в цепи протекает ток i= I_msin(ωt— φ). Отдаваемая источником в цепь за период Тсредняя мощность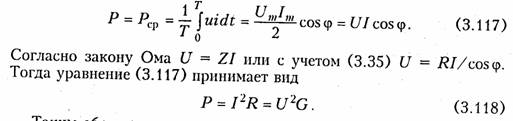



Таким образом, средняя за период мощность Рравна мощности, рассеиваемой на резистивном сопротивлении (проводимости) цепи. В этой связи мощность Рносит название активнойи измеряется в ваттах (Вт).

Кроме активной мощности Рв цепях гармонического токаиспользуют понятие реактивной мощности



Это отношение в энергетике называется коэффициентом мощности (косинусом φ) и является важной характеристикой электрических машин и линий электропередачи.  Чем выше cos φ,  тем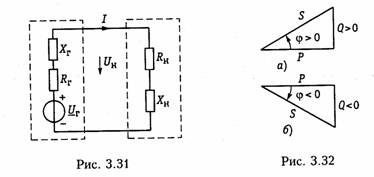



меньше потери энергии в линии и выше степень использования электрических машин и аппаратов. Максимальное значение cos φ = 1, при этом Р =S,Q= 0, т. е. цепь носит чисто активный характер и сдвиг фаз между током iи напряжением иравен нулю. Условие передачи максимальной мощности от генератора в нагрузку можно найти из условия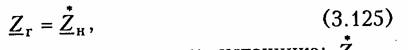



где Zj— комплексное внутреннее сопротивление источника; Z_H — комплексно-сопряженное сопротивление нагрузки. Это условие следует непосредственно из рассмотрения эквивалентной схемы, приведенной на рис. 3.31. Ток в данной цепи достигает максимума при Х_г = — Х_Hи выполнении условия R_Г= R_H(см. § 2.6), что и доказывает равенство (3.125). При этом мощность в нагрузке будет определяться уравнением



По аналогии с треугольниками токов и напряжений, сопротивлений и проводимостей (§§ 3.4 и 3.5) можно ввести треугольники мощностей.Так согласно (3.121) и (3.122) треугольник мощностей для цепи, носящий индуктивный характер будет иметь вид, изображенный на рис. 3.32, а,а для цепи с емкостным характером — на рис. 3.32, б.

Рассмотрим условие баланса мощности в цепях при гармоническом воздействии. В силу справедливости первого и второго законов Кирхгофа для комплексных действующих значений тока Iи напряжений U_в каждой из ветвей рассматриваемой цепи можно записать теорему Телледжена (1.35) в комплексной форме:



Однако поскольку ЗТК справедлив и по отношению к сопряженным токам 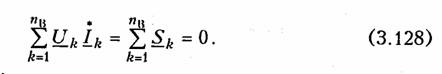то уравнение (3.127) можно записать в виде



Уравнение (3.128) отражает баланс комплексной мощности, согласно которому сумма комплексных мощностей, потребляемых всеми ветвями цепи, равна нулю. Баланс комплексной мощности можно сформулировать и в другой форме: сумма комплексных мощностей, отдаваемых независимыми источниками, равна сумме комплексных мощностей, потребляемых остальными ветвями электрической цепи:



Условие баланса активных мощностей непосредственно вытекает из закона сохранения энергии.

2.10. Модели электрических цепей

с зависимыми источниками

 

Интегрирующие и дифференцирующие цепи.Интегрирующие и дифференцирующие цепинаходят широкое применение в различных устройствах импульсной и вычислительной техники для формирования линейно изменяющихся напряжений и токов, селекции сигналов, линейного преобразования различных импульсов и т. д. Интегрирующая цепь описывается уравнением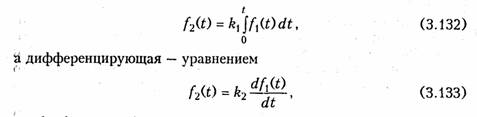



где k₁,k₂ — коэффициенты пропорциональности.

Простейшая интегрирующая и дифференцирующая цепи могут быть реализованы на базе RС-цепочки (рис. 3.33, 3.34). Действительно, если параметры интегрирующей цепочки (рис. 3.33) тако-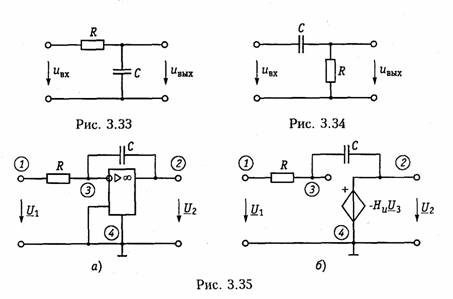



вы, что 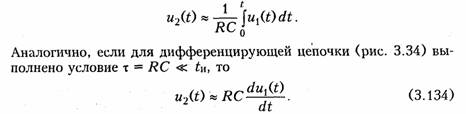где t_Идлительность входного сигнала, то на выходе такой цепи имеем



Однако точность интегрирования и дифференцирования такой пассивной цепи невысока. Поэтому на практике операции (3.132) и (3.133) реализуют с помощью активных цепей с зависимыми источниками, например на базе ОУ.

На рис. 3.35, аизображена схема интегратора, а на рис. 3.36, а —дифференциатора на ОУ. Определим комплексное действующее напряжение на выходе интегратора. Для этого воспользуемся эквивалентной схемой замещения ОУ в виде ИНУНа (рис. 3.35, б).

Приняв потенциал базисного узла V₄=О составим уравнение равновесия узловых потенциалов: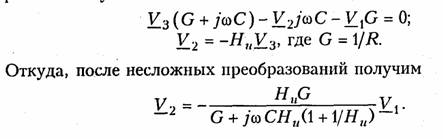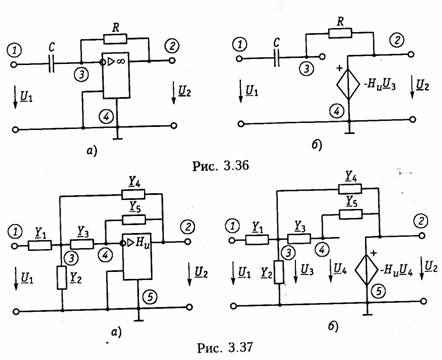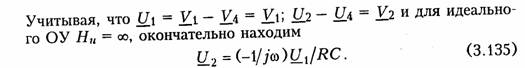    







А так как деление U₁на jω соответствует операции интегрирования входного сигнала u₁(t)(см. § 3.6), то схема, изображенная на рис. 3.34 является моделью идеального интегратора.

Аналогично можно получить для идеального дифференциатора (см. рис. 3.36):



т. е. u₁(t)и u₂(t) связаны между собой зависимостью, аналогичной (3.134). Знак «—» в уравнении (3.135) и (3.136) обусловлен поворотом на угол я фазы входного сигнала поданного на инвертирующий вход ОУ.