ману электротех. 1 Ток, напряжение, мощность

• Название: 1 Ток, напряжение, мощность
• Анкор: ману электротех.docx
• Дата: 24.03.2018
• Размер: 5.71 Mb.
• Имя файла: ману электротех.docx
• Тип: Документы; #17155
• страница: 5 из 15

Пример.Составим уравнение узловых потенциалов в матричной форме для схемы, изображенной на рис. 2.8, а.Примем за базис нулевой узел Vo ⁼ 0. Структурная матрица Ао в этой цепи в соответствии с правилом, изложенным в § 1.3, имеет вид



Подставив G_y и I_У в (2.33), получим уравнение узловых потенциалов в матричной форме. После определения матрицы узловых потенциалов V_y найдем матрицу напряжений ветвей согласно (2.30) и токи ветвей по закону Ома (2.17).

Для решения матричных уравнений в (2.23) или (2.33) обычно используют ЭВМ (см. § 2.7).

1.16. Метод эквивалентного генератора

 

Метод эквивалентного генератора базируется на теореме об активном двухполюснике (см. § 1.8) и позволяет упростить решение многих задач, связанных с передачей сигналов и электрической энергии от источника к приемнику. При этом обычно источник рассматривается как активный двухполюсник с известными задающими напряжениями U_Гили током I_г и внутренними сопротивлением R_Гили проводимостью G_Г, а приемник — как пассивный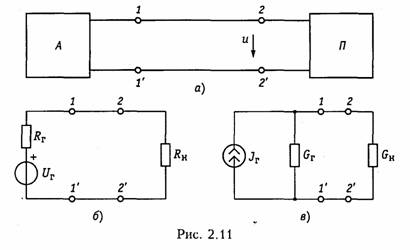



двухполюсник с внутренним сопротивлением нагрузки R_Hили проводимостью G_H (рис. 2.11).

            Таким образом, система передачи, изображенная на рис. 2.11, аможет быть представлена в виде двух эквивалентных схем: с источником напряжения (рис. 2.11, б) и с источником тока (рис. 2.11, в).

В соответствии с теоремами Тевенина и Нортона (см. § 1.8) задающее напряжение генератора определяется как напряжение холостого хода на разомкнутых зажимах активного двухполюсника U_Г=Uxx, а задающий ток — как ток короткого замыкания J_г  = I_КЗ. Внутреннее сопротивление активного двухполюсника R_Гили его проводимость G_г находятся как эквивалентные входные сопротивления или проводимость относительно разомкнутых зажимов пассивного двухполюсника, который получается после исключения из схемы всех источников напряжения и тока. При этом идеальные источники напряжения заворачиваются, а тока — размыкаются; реальные же источники заменяются своими внутренними сопротивлениями или проводимостями.

Параметры U_хх, Iкз, R_Г, G_Г можно найти как экспериментальным, так и расчетным путем. После нахождения параметров эквивалентного генератора напряжения или тока, ток I и напряжение Uв нагрузке можно найти для схемы, изображенной на рис. 2.9, б, по формуле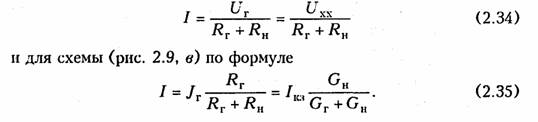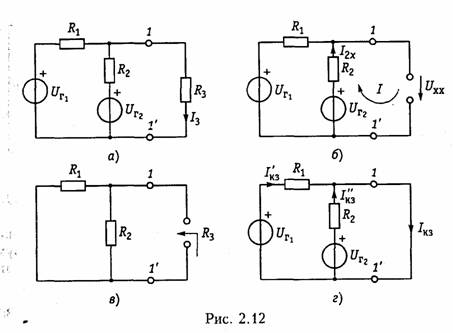





Пример.Найти ток в сопротивлении R₃(рис. 2.12, а) методом эквивалентного источника напряжения.

Разомкнем ветвь с R₃и определим U_хх (рис. 2.12, б) по ЗНК для I контура:



Очевидно, методы эквивалентного источника как напряжения так и тока дают один и тот же результат. Применение того или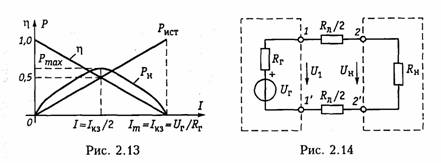



иного метода определяется удобством и простотой нахождения U_Xx или I_кз.

Одной из важнейших практических задач является оптимальная передача электрической энергии от активного к пассивному двухполюснику. Оптимум обычно понимается в смысле получения максимальной мощности в нагрузке Р_H. Мощность Р_нопределим как



Из (2.37) видно, что сопротивление линии существенно снижает мощность, отдаваемую в нагрузку, за счет потерь в линии.

 

 

2.1.Гармонические колебания. Основные понятия и определения

 

Электрические цепи могут находиться под воздействием постоянных или переменных напряжений и токов. Среди этих воздействий важнейшую роль играют гармонические колебания. Последние широко используются для передачи сигналов и электрической энергии, а также могут применяться в качестве простейшего испытательного сигнала. Исследование режима гармонических колебаний важно и с методической точки зрения, поскольку анализ электрических цепей при негармонических воздействиях можно свести к анализу цепи от совокупности гармонических воздействий. В этом смысле методику анализа и расчета цепей при гармонических воздействиях можно распространить и на цепи при периодических несинусоидальных, а также непериодических воздействиях (см. гл. 5, 9).

Гармоническое колебание i(t)(рис. 3.1) характеризуется следующими основными параметрами: амплитудой I_т;угловой частотой ω, начальной фазой φ_i. Амплитудойназывают максимальное абсолютное значение тока i(t).Аналитически гармоническое колебание можно записать в виде



где 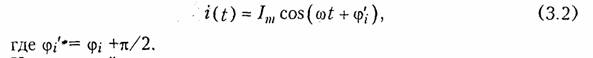 — называется текущей фазой(или просто фазой) гармонического колебания, так как она растет линейно во времени с угловой скоростью Вместо формулы (3.1) гармоническое колебание можно выразить и в косинусоидальной форме:



Наименьший промежуток времени, по истечении которого значения функции i(t) повторяются, называется периодом Т.Между периодом Ти угловой частотой ω существует простая связь:

Величину,   обратную периоду,   называют циклической частотой:f= 1/Т.Из вышеизложенного следует, что ω = 2πf. Единицей ■ измерения частоты fявляется герц (Гц), угловой частоты ω — радиан в секунду (рад/с). Так как радиан — величина безразмерная, то [ω] измеряется в 1/с или с^-1.

В радиотехнике и электросвязи используют гармонические сигналы от долей герц (инфранизкие частоты) до десятков и сотен гигагерц (сверхвысокие частоты).

Для питания различных электроэнергетических установок в России и ряде других стран принята промышленная частота f= 50 Гц. В качестве источников гармонических колебаний промышленной частоты используются электромашинные генераторы различного типа. Принцип работы простейшего электромашинного генератора иллюстрирует рис. 3.2. В состав генератора входят: статор, создающий магнитное поле с магнитной индукцией В, и ротор, вращающийся в этом магнитном поле с угловой частотой ω. При пересечении витками катушки ротора магнитного потока Ф в них согласно закону электромагнитной индукции наводится ЭДС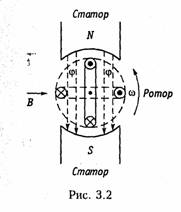       





где  ψ= wФ— потокосцепление катушки с магнитными потоками; w—число витков катушки. При постоянной скорости вращения ротора для получения ЭДС синусоидальной формы применяются полюса специальной формы. Частота на выходе генератора



где р_п— число пар полюсов ротора; v— частота вращения ротора, об/мин.

Электромашинные генераторы используются для получения гармонических напряжений и токов не выше 5...8 кГц. Для получения гармонических сигналов более высоких частот обычно используются ламповые и полупроводниковые генераторы (см. гл. 15).

Важными параметрами гармонических колебаний являются их действующее и среднее значения. Действующее значениегармонического тока



Действующие  значения токов  и  напряжений  называют еще  их среднеквадратическими значениями.

Определим тепловую энергию, которая выделяется гармоническим колебанием  i(t)за период Тв резистивном элементе с сопротивлением R: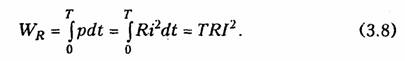



Таким образом, действующее значение тока численно равно такому постоянному току, который за период Тна том же сопротивлении выделяет то же количество тепла, что и гармонический ток.

Среднее значениегармонического тока



Подставив значение iиз (3.6) в (3.9), находим, что I_ср = 0. Этот результат вполне понятен, если учесть, что уравнение (3.9) определяет площадь, ограниченную кривой i(t)за период Т(см. рис. 3.1). Если значение тока определено за полпериода, то можно записать: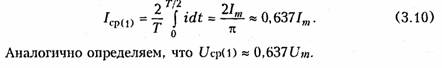



2.2. Способы представления гармонических колебаний

 

Гармонические колебания можно представить различными способами: функциями времени (временные диаграммы) (см. рис. 3.1); вращающимися векторами (векторные диаграммы); комплексными числами; амплитудными и фазовыми спектрами. Тот или иной способ представления применяется в зависимости от характера решаемых задач.

Временное представление гармонических колебаний наглядно, однако его использование в задачах анализа цепей затруднительно, так как требует проведения громоздких тригонометрических преобразований. Более удобно векторное представление гармонических колебаний, при котором каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой. В качестве примера на рис. 3.3 показано векторное представление двух колебаний токов i₁ и i₂: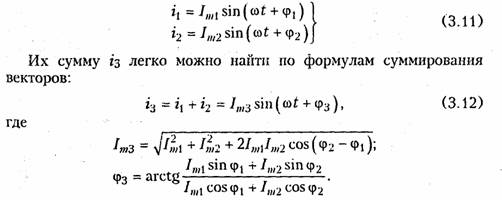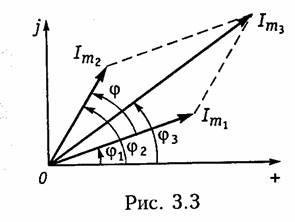





Величина φ= φ₂ —φ₁ называется фазовым сдвигом между колебаниями i₁ и i₂.Он определяется только начальными фазами φ₂ и φ₁ и не зависит от начала отсчета времени. Нетрудно видеть, что суммирование (наложение) любого числа гармонических колебаний с частотой со приводит к гармоническому колебанию той же частоты со.

Совокупность   векторов,   изображающих гармонические колебания в электрической цепи, называют векторной диаграммой.Векторные диаграммы можно строить как для амплитудных, так и для действующих значений токов и напряжений.

Наиболее распространенными являются представления гармонических колебаний с помощью комплексных чисел. Эти представления лежат в основе символического метода расчета электрических цепей — метода комплексных амплитуд.Представим ток i,определяемый формулой (3.6), на комплексной плоскости. Для этого изобразим вектор I_тна комплексной плоскости с учетом начальной фазы φ_i (рис. 3.4, а).Знаком «+» обозначено положительное направление вещественной оси, а j = √-1— положительное направление мнимой оси. Будем вращать этот вектор в положительном направлении (против часовой стрелки) с угловой частотой со. Тогда в любой момент времени положение вращающегося вектора определится комплексной величиной (комплексным гармоническим колебанием):



Первая часть слагаемого (3.13) отражает проекцию вращающегося вектора на вещественную ось, а вторая часть — на мнимую ось. Сравнив второе слагаемое в (3.13) с (3.6), приходим к выводу: синусоидальный ток iна комплексной плоскости представляется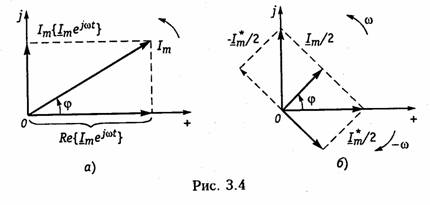



в форме проекции иа мнимую ось вращающегося вектора (3.13)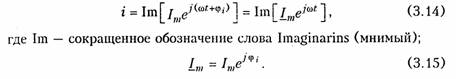



Величина I_тносит название комплексной амплитуды тока.

Важным свойством комплексной амплитуды является то, что она полностью определяет гармоническое колебание заданной частоты ω, так как содержит информацию об его амплитуде и начальной фазе.

Если гармоническое колебание задается в форме косинусоиды, например



где -сопряжение комплексная амплитуда тока.

Таким образом, ток iиз (3.6) согласно (3.19) можно представить как геометрическую разность векторов  вращающихся в противоположных направлениях с угловой частотой со, а ток из (3.16) — как геометрическую сумму этих векторов (рис. 3.4, б). В первом случае iрасполагается на мнимой, а во втором случае — на действительной осях. Комплексную амплитуду синусоидальной функции заданной частоты можно рассматривать как преобразование временной функции в частотную область.



 

Спектральное (частотное) представление гармонических колебаний состоит в задании амплитудного и фазового спектров колебания (рис. 3.5). Более подробно спектральное представление и методы анализа цепей, основанные на этом, представлении, рассмотрены в гл. 5, 9.

 

2.3. Гармонические колебания в резистивных, индуктивных и емкостных элементах

 

Резистивные цепи.Пусть к резистивному элементу Rприложено гармоническое напряжение



При последовательном или параллельном соединениях нескольких резистивных элементов ток в цепи определяется уравнением, аналогичным (3.22), где Rопределяется согласно (1.22) для последовательного и (1.27) для параллельного соединений элементов. При этом фазовый сдвиг между током и приложенным напряжением остается равным нулю.

Индуктивные цепи.Под действием напряжения (3.21) в индуктивном элементе будет протекать ток согласно (1.9):







Величину, обратную X_L,называют индуктивной проводимостью BL= l/(ωL). Как следует из полученных выражений, ток в индуктивности отстает от приложенного напряжения на π/2, т. е. фазовый сдвиг между током iи напряжением и(рис. 3.6, б)



На векторной диаграмме фазовый сдвиг φ откладывается от вектора тока к вектору напряжения. Нетрудно видеть, что средняя за период мощность в индуктивном элементе равна нулю.

При последовательном и параллельном соединениях индуктивных элементов ток в цепи определяется уравнением, аналогичным (3.24), где Lнаходится согласно (1.23) для последовательного и (1.29) для параллельного соединений.