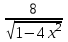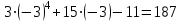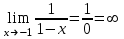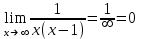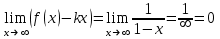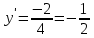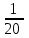|
|
сор соч алгебра 10класс. сор соч алгебра 10 кл папка. Алгебра и начала анализа Суммативное оценивание за раздел Функция, ее свойства и график
1. Разложить многочлен х4+х3-6х2 на множители
2. Вычислите предел функции:
a) 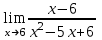 ; ;
b) 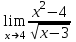 ; ;
c) 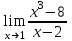 . .
3. Найдите производную функции y= 3arccos 2x
4. Используя теорему Безу, найдите остаток от деления многочлена:
5x2 – 3x + 7 на двучлен (x – 2)
5. Найдите асимптоты графика функции f(x)=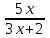
6. Составьте уравнение касательной к графику функции y=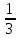 x3-4x+1 в точке М(3;-2) x3-4x+1 в точке М(3;-2)
7. Найдите сумму коэффициентов многочлена, который образуется после раскрытия скобок в выражении (2-3x+x2)1969 * (2+3x+x2)1970
8. Дано y=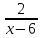 , dy=0,025, x0=2. , dy=0,025, x0=2.
Найти ∆х.
Схема выставления баллов
№
|
Ответ
|
Балл
|
Дополнительная информация
|
1
|
х2(х2+х-6)
|
1
|
Принимается альтернативное разложение на множители
|
х2 + x – 6 = 0
х1,2=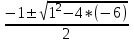
|
1
|
х1=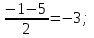 х2= х2=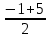 =2 =2
|
1
|
(х+3)(х-2)
|
1
|
2
|
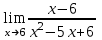 =0 =0
|
1
|
|
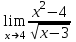 = = 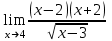 = =
|
1
|
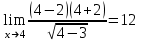
|
1
|
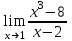 = =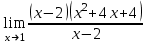
|
1
|
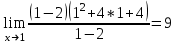
|
1
|
3
|
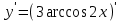 = -3* = -3*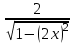 = - = -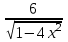
|
2
|
|
4
|
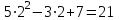
|
1
|
|
5
|
3x+2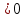 , 3x , 3x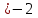 , x , x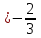
|
1
|
|
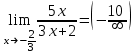
|
1
|
k=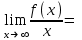 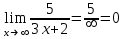
|
1
|
b=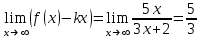 
|
1
|
y=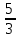
|
6
|
f(3)=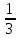 *33-4*3+1=-2 *33-4*3+1=-2
|
1
|
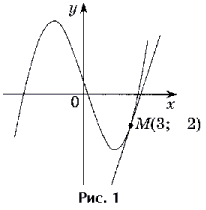
|
a=3-абсцисса касания
f(3)=-2
|
1
|
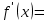 x2-4 x2-4
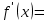 5 5
|
1
|
y=-2+5(x-3)
y=5x-17 – уравнение касательной
|
1
|
7
|
Сумма коэффициентов многочлена, который получится после раскрытия скобок и приведения всех подобных членов, равна значению этой функции при x = 1
f(x)= (2-3x+x2)1969 * (2+3x+x2)1970
|
1
|
Принимается только применение теоремы Безу
|
f(1)=(2-3*1+12)1969 * (2+3*1+12)1970=0
|
1
|
8
|
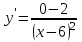 = = 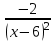 или эквивалент или эквивалент
|
1
|
|
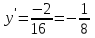
|
1
|
dy=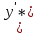 ∆х ∆х
∆х=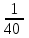 * (-8)= - * (-8)= -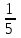
|
1
|
ВАРИАНТ 2
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Количество баллов
|
4
|
5
|
2
|
1
|
4
|
4
|
2
|
3
|
Всего баллов
|
25 баллов
|
1. Разложить многочлен 4х3+8х2-х на множители
2. Вычислите предел функции:
a) 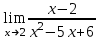 ; ;
b) 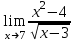 ; ;
c) 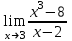 . .
3. Найдите производную функции y= 4arccos 2x
4. Используя теорему Безу, найдите остаток от деления многочлена:
3x4 + 15x – 11 на двучлен (x + 3)
5. Найдите асимптоты графика функции f(x)=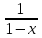
6. Составьте уравнение касательной к графику функции y=x3-4x+1 в точке М(3;-2)
7. Найдите сумму коэффициентов многочлена, который образуется после раскрытия скобок в выражении (х5+x4-2)2012 * (х2-x+2)2011
8. Дано y=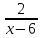 , dy=0,025, x0=4. , dy=0,025, x0=4.
Найти ∆х.
Схема выставления баллов
№
|
Ответ
|
Балл
|
Дополнительная информация
|
1
|
х(4х2+8х-1)
|
1
|
Принимается альтернативное разложение на множители
|
х=0, х2 + x – 6 = 0
х1,2=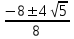
|
1
|
х1=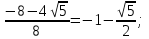
х2=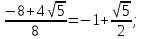
|
1
|
4х(х+1-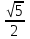 )(х+1+ )(х+1+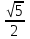 ) )
|
1
|
2
|
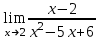 =0 =0
|
1
|
|
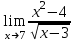 = = 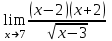 = =
|
1
|
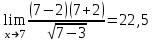
|
1
|
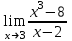 = =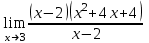
|
1
|
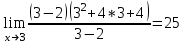
|
1
|
3
|
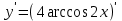 = -4* = -4*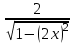 = - = -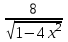
|
2
|
|
4
|
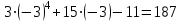
|
1
|
|
5
|
1-х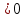 , х , х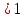
|
1
|
|
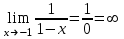
|
1
|
k=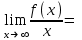 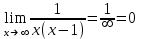
|
1
|
b=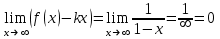 
|
1
|
y=0-горизонтальная асимптота
|
6
|
f(3)=33-4*3+1=-16
|
1
|
|
a=3-абсцисса касания
f(3)=16
|
1
|
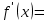 3x2-4 3x2-4
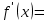 23 23
|
1
|
y=-16+23(x-3)
y=23x-53 – уравнение касательной
|
1
|
7
|
Сумма коэффициентов многочлена, который получится после раскрытия скобок и приведения всех подобных членов, равна значению этой функции при x = 1
f(x)= (х5+х4-2)2012 * (х2-х+2)2011
|
1
|
Принимается только применение теоремы Безу
|
f(1)= (15+14-2)2012 * (12-1+2)2011=0
|
1
|
8
|
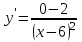 = = 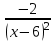 или эквивалент или эквивалент
|
1
|
|
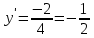
|
1
|
dy=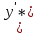 ∆х ∆х
∆х=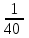 * (-2)= - * (-2)= -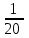
|
1
|
|
|
|
 Скачать 0.87 Mb.
Скачать 0.87 Mb.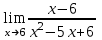 ;
; 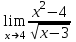 ;
; 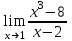 .
. 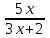
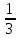 x3-4x+1 в точке М(3;-2)
x3-4x+1 в точке М(3;-2) 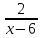 , dy=0,025, x0=2.
, dy=0,025, x0=2. 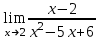 ;
; 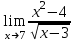 ;
; 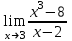 .
. 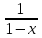
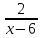 , dy=0,025, x0=4.
, dy=0,025, x0=4. 
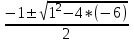
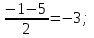 х2=
х2=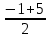 =2
=2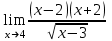 =
=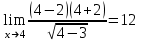
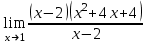
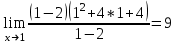
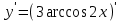 = -3*
= -3*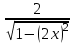 = -
= -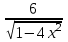
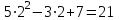
 , 3x
, 3x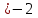 , x
, x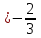
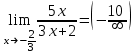
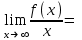
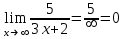
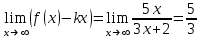

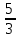

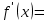 x2-4
x2-4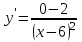 =
= 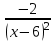 или эквивалент
или эквивалент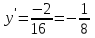
 ∆х
∆х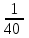 * (-8)= -
* (-8)= -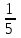
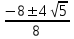
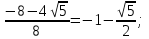
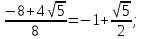
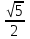 )(х+1+
)(х+1+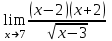 =
=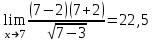
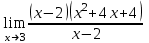
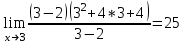
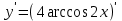 = -4*
= -4*