сор соч алгебра 10класс. сор соч алгебра 10 кл папка. Алгебра и начала анализа Суммативное оценивание за раздел Функция, ее свойства и график

• Название: Алгебра и начала анализа Суммативное оценивание за раздел Функция, ее свойства и график
• Анкор: сор соч алгебра 10класс
• Дата: 07.11.2022
• Размер: 0.87 Mb.
• Имя файла: сор соч алгебра 10 кл папка.docx
• Тип: Документы; #773784
• страница: 11 из 12

СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ

Обзор суммативного оценивания за 4 четверть

Продолжительность – 40 минут

Количество баллов – 20

Типы заданий:

КО – задания, требующие краткого ответа;

РО – задания, требующие развернутого ответа.

Структура суммативного оценивания

Данный вариант состоит из 6 заданий, включающих вопросы с кратким и развернутым

ответом.

В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде

численного значения, слова или короткого предложения.

В вопросах, требующих развернутого ответа, обучающийся должен показать всю

последовательность действий в решении заданий для получения максимального балла.

Оценивается способность обучающегося выбирать и применять математические приемы в

ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов

ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ

Раздел	Проверяемая цель	Уровень мыслительных навыков	Кол. заданий*	№ задания*	Тип задания*	Время на выполнение, мин*	Балл*	Балл за раздел
Применение производной	10.4.1.26 Знать необходимое и достаточное условие возрастания (убывания) функции на интервале	Знание и понимание	1	1	КО	3		14
	10.4.1.33 Исследовать свойства функции с помощью производной и строить её график	Навыки высокого порядка
	10.4.1.30 Находить вторую производную функции	Применение	1	2	РО	6
	10.4.3.3 Решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции	Навыки высокого порядка	1	5	РО	12
Случайные величины и их числовые характеристики	10.3.2.10 Знать определение дискретной и непрерывной случайной величины и уметь их различать	Знание и понимание	1	3	КО	4		11
	10.3.2.12 Знать понятие математического ожидания дискретной случайной величины и его свойства	Знание и понимание	1	4	РО	7
	10.3.2.13 Вычислять математическое ожидание дискретной случайной величины	Применение
	10.3.2.14 Вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины	Применение	1	6	РО	8
ИТОГО:			6					25

ЗАДАНИЯ

1 ВАРИАНТ

Оценивание заданий работы
№ задания	1	2	3	4	5	6
Количество баллов	3	4	2	5	7	4
Всего баллов	25 баллов

1. Функция y =f (x) определена на интервале (1; 10). Используя график производной функции y =f (x) установите: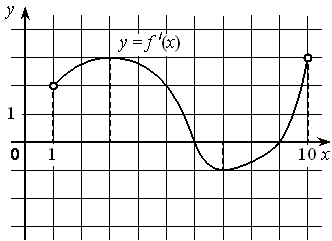



а) промежутки возрастания функции y =f (x);

b) точки минимума функции.

2. Найдите вторую производную функции: a) у=х·lnx;

b) y=x⁴ -4x³-8x²+12

3. Из приведенных ниже примеров выберите 2 примера дискретных случайных величин:

a) измерение скорости перемещения любого вида транспорта;

b) сумма очков при бросании двух игральных костей;

c) число бракованных деталей в партии;

d) измерение температуры в течение конкретного интервала времени;

e) продолжительность человеческой жизни.

4. Для случайной величины Х с данным рядом распределения

Х	-1	0	1	8
р	0,2	0,1	р1	р2

a) найдите р₁ и р₂ так, чтобы М(Х)=0,5;

b) после этого вычислите М(3Х), пользуясь свойством математического ожидания.

5. Площадь прямоугольного участка 144 м². При каких размерах участка длина окружающего его забора будет наименьшей?

6. Случайная величина Х задана законом распределения:

X	4	6	6	12
p	0,143	0,2	0,49	0,167

Найти дисперсию случайной величины D(X).
2 ВАРИАНТ

Оценивание заданий работы
№ задания	1	2	3	4	5	6
Количество баллов	3	4	2	5	7	4
Всего баллов	25 баллов

1. Функция y =f (x) определена на интервале (-8; 8). Используя график производной функции y =f (x) установите: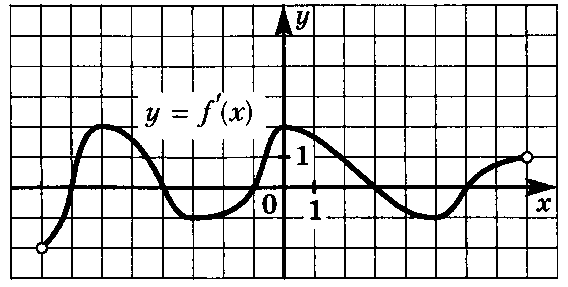




а) промежутки возрастания функции y =f (x);

b) точки минимума функции.

2. Найдите вторую производную функции: a) y=e^x· lnх;

b) y= 5x⁵+3x³

3. Из приведенных ниже примеров выберите 2 примера дискретных случайных величин:

a) температура воздуха в течение дня;

b) время инкубационного периода заболевания;

c) число учеников, отсутствующих в классе;  

d) расстояние, которое пролетит снаряд при выстреле;

e) среднее значение оценки за контрольную работу в классе.

4. (5 баллов) Для случайной величины Х с данным рядом распределения

Х	-5	2	3	4
р	0,4	р1	0,1	р2

а) найдите р₁ и р₂ так, чтобы М(Х)= 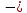0,3;

b) после этого вычислите М(3Х), пользуясь свойством математического ожидания.

5. Площадь прямоугольного треугольника 6 см². Найдите наименьшее значение площади квадрата, построенного на гипотенузе треугольника.
6. Случайная величина задана законом распределения:

X	5	7	7	13
p	0,143	0,2	0,49	0,167