|
сор соч алгебра 10класс. сор соч алгебра 10 кл папка. Алгебра и начала анализа Суммативное оценивание за раздел Функция, ее свойства и график
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ»
Тема
|
Предел функции в точке и на бесконечности. Асимптоты графика функции. Непрерывность функции в точке и на множестве. Первый замечательный предел
|
Цели обучения
|
10.4.1.14 Применять методы раскрытия неопределенностей вида 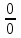 , , 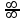 и при вычислении пределов и при вычислении пределов
10.4.1.15 Вычислять пределы, применяя первый замечательный предел 10.4.1.10 Знать определение асимптоты к графику функции и уметь составлять уравнения асимптот
10.4.1.13 Знать свойства непрерывных функций и применять их при доказательстве непрерывности функции
|
Критерии оценивания
|
Обучающийся:
Раскрывает неопределенности при вычислении пределов функции
Применяет первый замечательный предел
Составляет уравнения асимптот функции
Доказывает непрерывность функций, используя свойства непрерывных функций
|
Уровень мыслительных навыков
|
Применение
|
Время выполнения
|
20 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
Количество баллов
|
4
|
3
|
5
|
2
|
Всего баллов
|
14 баллов
|
1 ВАРИАНТ
1. Найдите значение предела:
а) 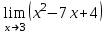 ; b) ; b) 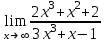
2. Вычислите значение предела:
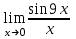
3. Дана функция 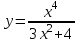
а)Запишите уравнение вертикальной асимптоты.
b) С помощью выделения целой части, найдите уравнение наклонной асимптоты.
c) Используя предел, покажите, что Вы верно нашли наклонную асимптоту.
4. Известно, что 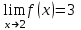 и и 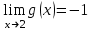 Определите, будут ли следующие функции непрерывными в точке 3: Определите, будут ли следующие функции непрерывными в точке 3:
a) 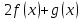 ; ;
b) 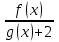
2 ВАРИАНТ
1. Найдите значение предела:
а) 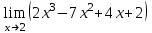 ; b) ; b) 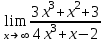
2. Вычислите значение предела:
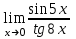
3. Дана функция 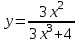
а)Запишите уравнение вертикальной асимптоты.
b) С помощью выделения целой части, найдите уравнение наклонной асимптоты.
c) Используя предел, покажите, что Вы верно нашли наклонную асимптоту.
4. Известно, что 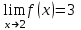 и и 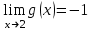 Определите, будут ли следующие функции непрерывными в точке 4: Определите, будут ли следующие функции непрерывными в точке 4:
a) 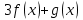 ; ;
b) 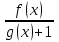
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Раскрывает неопределенности при вычислении пределов
|
1
|
раскладывает выражения на множители;
|
1
|
находит значение предела
|
1
|
делит на старшую степень переменной;
|
1
|
находит значение предела;
|
1
|
Применяет первый замечательный предел
|
2
|
выполняет преобразования;
|
1
|
использует первый замечательный предел;
|
1
|
находит значение предела;
|
1
|
Составляет уравнения асимптот функции
|
3
|
находит вертикальную асимптоту;
|
1
|
выделяет целую часть;
|
1
|
выполняет деление многочленов с остатком;
|
1
|
находит наклонную асимптоту;
|
1
|
использует условие для нахождения наклонной асимптоты;
|
1
|
Доказывает непрерывность функций, используя свойства непрерывных функций
|
4
|
определяет непрерывность суммы двух функций;
|
1
|
определяет непрерывность частного двух функций.
|
1
|
Итого:
|
14
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ»
ФИО ОБУЧАЮЩЕГОСЯ: ______________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Раскрывает неопределенности при вычислении пределов
|
Затрудняется в использовании методов раскрытия неопределенностей при вычислении пределов
|
Допускает ошибки при использовании методов раскрытия неопределенностей / вычислении пределов
|
Использует методы раскрытия неопределенностей при вычислении пределов
|
Применяет первый замечательный предел
|
Затрудняется в применении первого замечательного предела
|
Допускает ошибки при выполнении преобразований / вычислении предела с помощью первого замечательного предела
|
Выполняет преобразования и применяет первый замечательный предел
|
Составляет уравнения асимптот функции
|
Затрудняется в нахождении асимптот функций
|
Допускает ошибки при нахождении вертикальных / горизонтальных / наклонных асимптот функций
|
Находит асимптоты функций
|
Доказывает непрерывность функций, используя свойства непрерывных функций
|
Затрудняется в применении свойств непрерывных функций
|
Допускает ошибки при использовании свойств непрерывных функций / определении непрерывности функций
|
Применяет свойства непрерывных функций, доказывает непрерывность функций
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ «ПРОИЗВОДНЫЕ»
Тема
|
Определение производной. Правила нахождения производных. Производная сложной функции. Производные тригонометрических функций. Физический и геометрический смысл производной касательной к графику функции
|
Цели обучения
|
10.4.1.18 Находить производные постоянной функции и степенной функции
10.4.3.1 Решать прикладные задачи, опираясь на физический смысл производной
10.4.1.21 Знать и применять правила дифференцирования
10.4.1.25 Составлять уравнение касательной к графику функции в заданной точке
10.4.1.23 Находить производные тригонометрических функций
10.4.1.22 Находить производную сложной функции
|
Критерии оценивания
|
Обучающийся:
Находит производную степенной функции
Применяет физический смысл производной при решении задач
Применяет правила дифференцирования для нахождения производной
Составляет уравнение касательной к графику функции
Находит производную тригонометрической функции и производную сложной функции
|
Уровень мыслительных навыков
|
Применение
|
Время выполнения
|
20 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
Количество баллов
|
2
|
6
|
4
|
3
|
Всего баллов
|
15 баллов
|
1 ВАРИАНТ
1. Найдите производную функции: f(x)= 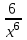 -4 -4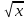
2. Точка движется прямолинейно по закону S (t) -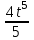 +8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 5;11 скорость движения точки будет наибольшей? Найдите величину этой скорости. +8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 5;11 скорость движения точки будет наибольшей? Найдите величину этой скорости.
3. Напишите уравнение касательной к графику функции у=5-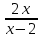 , проведённой через точку с абсциссой х0=1 , проведённой через точку с абсциссой х0=1
4. Вычислите значение производной функции f(x)=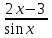 в точке x= в точке x=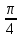 . .
2 ВАРИАНТ
1. Найдите производную функции: f(x)= 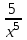 -6 -6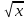
2. Точка движется прямолинейно по закону S (t) -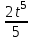 +8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 6;12 скорость движения точки будет наибольшей? Найдите величину этой скорости. +8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 6;12 скорость движения точки будет наибольшей? Найдите величину этой скорости.
3. Напишите уравнение касательной к графику функции у=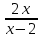 -3, проведённой через точку с абсциссой х0=1 -3, проведённой через точку с абсциссой х0=1
4. Вычислите значение производной функции f(x)=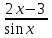 в точке x= в точке x=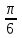 . .
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Находит производную степенной функции.
|
1
|
находит производную степени с отрицательным показателем;
|
1
|
находит производную степени с рациональным показателем;
|
1
|
Применяет физический смысл производной при решении задач.
|
2
|
находит первую производную функции;
|
1
|
находит вторую производную функции;
|
1
|
находит критические точки функции;
|
1
|
вычисляет значения функции в критических точках;
|
1
|
вычисляет значения функции скорости на концах отрезка;
|
1
|
находит наибольшее значение скорости на отрезке.
|
1
|
Составляет уравнение касательной к графику функции.
|
3
|
находит производную функции;
|
1
|
находит значение производной функции в точке;
|
1
|
находит значение функции в точке;
|
1
|
подставляет значения в формулу и записывает уравнение касательной;
|
1
|
Находит производную тригонометрической функции и производную сложной функции в точке.
|
4
|
использует правило нахождения производной частного;
|
1
|
находит производную синуса;
|
1
|
находит значение производной в точке.
|
1
|
Итого:
|
15
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ОТНОШЕНИЯ И ПРОПОРЦИИ»
ФИО ОБУЧАЮЩЕГОСЯ: ______________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Находит производную степенной функции.
|
Затрудняется в нахождении производной степени с отрицательным и рациональным показателем
|
Находит производную степени с отрицательным показателем/с рациональным показателем
|
Верно находит производную степени с отрицательным и рациональным показателем
|
Применяет физический смысл производной при решении задач.
|
Затрудняется в нахождении критических точек
|
Применяет формулы нахождения первой и второй производных и критические точки
|
Верно находит производные функции, вычисляет значения функции в критических точках;
вычисляет значения функции скорости на концах отрезка;
находит наибольшее значение скорости на отрезке.
|
Составляет уравнение касательной к графику функции.
|
Затрудняется в нахождении значения производной функции в точке
|
Допускает ошибки при нахождении производной функции, значении производной функции в точке, а также При нахождении значения функции в точке
|
Верно находит производную функции, значение производной функции в точке, находит значение функции в точке, подставляет значения в формулу и записывает уравнение касательной
|
Находит производную тригонометрической функции и производную сложной функции в точке.
|
затрудняется в использовании правила нахождения производной частного
|
Допускает ошибки при использовании правила нахождения производной частного и нахождении производной синуса
|
Верно находит производную тригонометрической функции и производную сложной функции в заданной точке.
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
Тема
|
Признаки возрастания и убывания функции. Критические точки и точки экстремума функции. Точки перегиба функции, выпуклость графика функции. Исследование функции с помощью производной и построение графика. Наибольшее и наименьшие значения функции на отрезке
|
Цели обучения
|
10.4.1.26 Знать необходимое и достаточное условие возрастания (убывания) функции на интервале
10.4.1.27 Находить промежутки возрастания (убывания) функции
10.4.1.28 Знать определения критических точек и точек экстремума функции, условие существования экстремума функции
10.4.1.31 Знать определение точки перегиба графика функции и необходимое и достаточное условие выпуклости вверх (вниз) графика функции на интервале
10.4.3.3 Решать прикладные задачи, связанные с нахождением наибольшего (наименьшего) значения функции
|
Критерии оценивания
|
Обучающийся
Использует условие возрастания (убывания) функции и находит промежутки монотонности
Использует определение точек экстремума функции
Решает задачи на нахождение наибольшего (наименьшего) значения функции
Находит точки перегиба графика функции
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
Количество баллов
|
3
|
5
|
6
|
Всего баллов
|
14 баллов
|
1 ВАРИАНТ
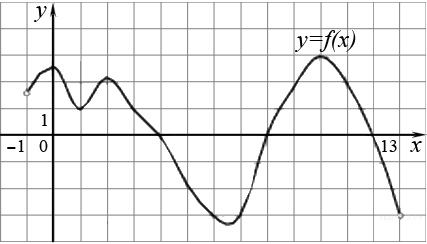
1. На рисунке изображен график функции y = f(x), определенной на интервале (−1; 13). Определите:
а. Количество целых точек, в которых производная функции отрицательна;
б. Количество точек, в которых касательная к графику функции параллельна прямой у = - 1;
с. Количество точек, в которых производная равна нулю;
2. Функция полных издержек производства имеет вид 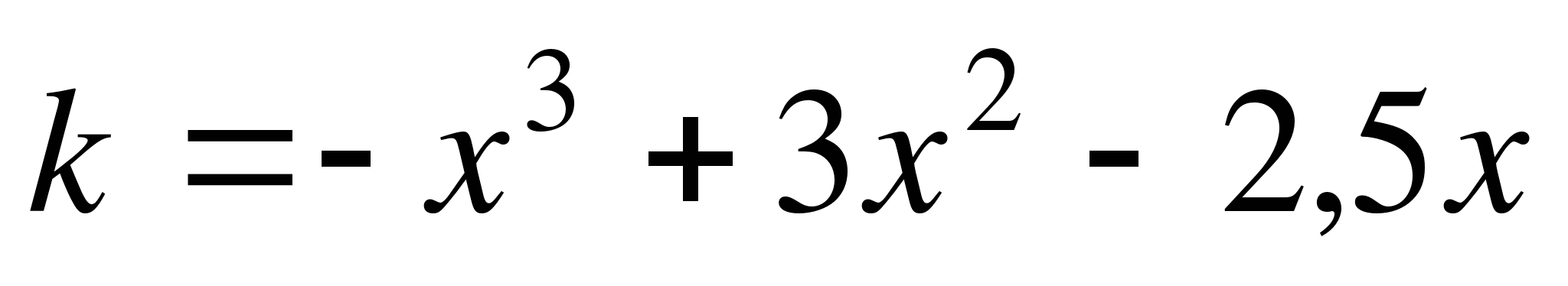 где где 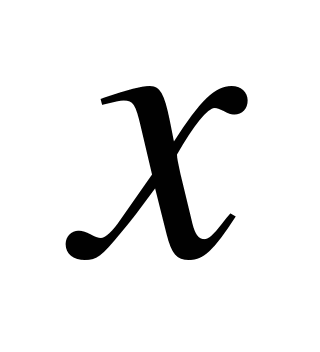 - объем производства продукции в условных единицах для данного производства. Определите, при каком объеме производства продукции средние издержки производства будут иметь наибольшее значение? - объем производства продукции в условных единицах для данного производства. Определите, при каком объеме производства продукции средние издержки производства будут иметь наибольшее значение?
3. Определите промежутки выпуклости вверх(вниз) и точки перегиба данной функций:
f(x)=x4-4x3-18x2-2x+3
2 ВАРИАНТ
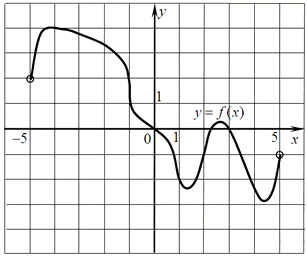
1. На рисунке изображен график функции у = f (х), определенной на интервале (−5; 5). Определите:
а. Количество целых точек, в которых производная функции положительна;
б. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 1;
с. Количество точек, в которых производная равна нулю;
2. Потребление электроэнергии предприятиями и населением города с 8 ч до 18 ч описывается формулой 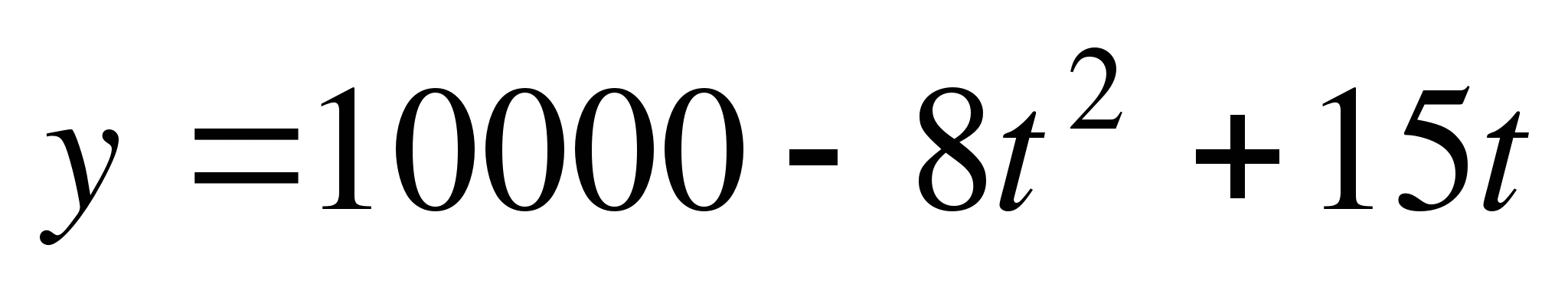 , где , где 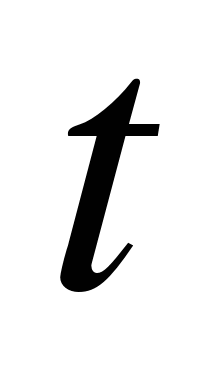 - время в часах. В какой момент времени потребление энергии будет наибольшим? - время в часах. В какой момент времени потребление энергии будет наибольшим?
3. Определите промежутки выпуклости вверх(вниз) и точки перегиба данной функций:
f(x)=x4+4x3-18x2-+x-17
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Использует условие возрастания (убывания)
функции и находит промежутки монотонности
|
1
|
определяет количество целых точек, в которых производная функции отрицательна(положительна)
|
1
|
определяет количество точек, в которых касательная к графику функции параллельна данной прямой
|
1
|
определяет количество точек, в которых производная равна нулю
|
1
|
Решает задачи на нахождение наибольшего
(наименьшего) значения функции
|
2
|
находит первую производную
|
1
|
определяет критические точки
|
1
|
находит знак второй производной в критической точке
|
1
|
проверяет с помощью производной является ли значение наибольшим (наименьшим)
|
1
|
записывает ответ в связи с условием задачи
|
1
|
Находит точки
перегиба графика
функции, интервалы выпуклости вверх (вогнутости вниз) графика функции.
|
3
|
находит первую производную
|
1
|
находит вторую производную функции;
|
1
|
составляет выражение для определения точек перегиба;
|
1
|
находит точки перегиба функции.
|
1
|
составляет выражение для определения выпуклости графика функции;
|
1
|
находит интервалы выпуклости вверх (вогнутости вниз) графика функции.
|
1
|
Общий балл
|
14
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ»
ФИ ОБУЧАЮЩЕГОСЯ_______________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Использует условие возрастания (убывания) функции и находит промежутки монотонности
|
Затрудняется в использовании условия возрастания (убывания) функции
|
Допускает ошибки при использовании условий возрастания /убывания функции определении промежутков возрастания / убывания
|
Использует условие возрастания (убывания) функции
|
Решает задачи на нахождение наибольшего (наименьшего) значения функции
|
Затрудняется в решении задач на определение максимума (минимума)
|
Допускает ошибки при решении задач на нахождение максимума (минимума)вычислительные ошибки
|
Решает задачи на определение
максимума (минимума)
|
Находит точки перегиба графика функции, интервалы выпуклости вверх (вогнутости вниз) графика функции.
|
Затрудняется в определении
точек перегиба графика функции и определения интервалов выпуклости вверх (вниз)
|
Допускает ошибки при определении точек перегиба графика функции и определения интервалов выпуклости вверх (вниз)
|
Определяет точки перегиба
графика функции и определения интервалов выпуклости вверх (вниз)
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ ЗА РАЗДЕЛ
«СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ»
Тема
|
Дискретные случайные величины. Числовые характеристики дискретных случайных
Величин. Виды распределения дискретных случайных величин. Закон больших чисел
|
Цели обучения
|
10.3.2.11 Составлять таблицу закона распределения некоторых дискретных случайных величин
10.3.2.13 Вычислять математическое ожидание дискретной случайной величины
10.3.2.14 Вычислять дисперсию и среднее квадратическое (стандартное) отклонение дискретной случайной величины
|
Критерии оценивания
|
Обучающийся
Использует закон распределения дискретных случайных величин
Находит математическое ожидание дискретной случайной величины
Вычисляет дисперсию и стандартное отклонение дискретной случайной величины
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
20 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
Количество баллов
|
9
|
6
|
Всего баллов
|
15 баллов
|
1 ВАРИАНТ
Закон распределения дискретной случайной величины X имеет вид:
хi
|
-2
|
-1
|
0
|
1
|
2
|
pi
|
0,2
|
0,1
|
0,2
|
p4
|
p5
|
a) Найдите значение p.
b) Найдите вероятность P(x < 0).
c) Вычислите математическое ожидание M(X.)
d) Вычислите значение 3∙M(X).
e) Вычислите дисперсию.
f) Вычислите стандартное отклонение случайной величины X.
2. Вероятность выпуска прибора, удовлетворяющего требованиям качества, равна 0,9. В контрольной партии 3 прибора. Случайная величина X– число приборов, удовлетворяющих требованиям качества.
а) найти закон распределения указанной случайной величины X и ее функцию распределения F(x).
b) вычислить математическое ожидание M(x), дисперсию D(x) и среднее квадратическое отклонение 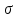 (x) (x)
2 ВАРИАНТ
Дискретная случайная величина X задана законом распределения:
хi
|
-2
|
-1
|
3
|
8
|
9
|
pi
|
4p
|
0,2
|
0,3
|
p
|
0,4
|
a) Найдите значение p.
b) Найдите вероятность P(x <3).
c) Вычислите математическое ожидание M(X.)
d) Вычислите значение 2∙M(X).
e) Вычислите дисперсию.
f) Вычислите стандартное отклонение случайной величины X.
Вероятность выхода из строя каждого из трех блоков прибора в течение гарантийного срока равна 0,3. Случайная величина X–число блоков, вышедших из строя в течение гарантийного срока.
найти закон распределения указанной случайной величины X и ее функцию распределения F(x).
вычислить математическое ожидание M(x), дисперсию D(x) и среднее квадратическое отклонение 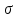 (x) (x)
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Использует закон
распределения
дискретных случайных
величин
|
1a
|
составляет выражение, используя закон
распределения;
|
1
|
находит значение параметра;
|
1
|
1b
|
находит вероятность;
|
1
|
определяет все значения случайно
величины;
|
1
|
2a
|
находит вероятности минимум в трех
случаях;
|
1
|
находит вероятности во всех случаях;
|
1
|
Находит математическое
ожидание дискретной
случайной величины
|
1c
|
использует формулу математического
ожидания;
|
1
|
вычисляет математическое ожидание;
|
1
|
1d
|
использует свойства математического
ожидания;
|
1
|
2b
|
использует математическое ожидание;
|
1
|
находит ответ;
|
1
|
Вычисляет дисперсию и
стандартное отклонение
дискретной случайной
величины
|
1e,2b
|
использует формулу дисперсии
(подставляет произведение суммы
квадратов значений случайных величин
на их вероятность);
|
1
|
использует формулу дисперсии
(подставляет математическое ожидание);
|
1
|
вычисляет дисперсию;
|
1
|
|
1f,2b
|
находит стандартное отклонение.
|
1
|
Общий балл
|
15
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ»
ФИ ОБУЧАЮЩЕГОСЯ_______________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Использует закон
распределения дискретных
случайных величин
|
Затрудняется в составлении и использовании закона распределения дискретных
случайных величин
|
Допускает вычислительные ошибкипри составлении / использовании закона распределения дискретных
случайных величин
|
Cоставляет и использует закон
распределения дискретных
случайных величин
|
Находит математическое
ожидание дискретной
случайной величины
|
Затрудняется в нахождении
математического ожидания
дискретной случайной
величины
|
Допускает вычислительные ошибки при нахождении математического ожидания дискретной случайной величины
|
Находит математическое
Ожидание дискретной случайной величины
|
Вычисляет дисперсию и
стандартное отклонение
дискретной случайной
величины
|
Затрудняется в вычислении
дисперсии и стандартного
отклонения дискретной
случайной величины
|
Допускает вычислительные ошибки при нахождении дисперсии /стандартного отклонения дискретной случайной величины
|
Вычисляет дисперсию истандартное отклонение дискретной случайной величины
|
|
|
|
 Скачать 0.87 Mb.
Скачать 0.87 Mb.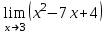 ; b)
; b) 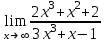
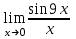
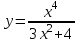
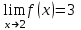 и
и 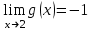 Определите, будут ли следующие функции непрерывными в точке 3:
Определите, будут ли следующие функции непрерывными в точке 3: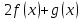 ;
;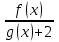
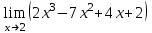 ; b)
; b) 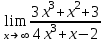
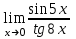
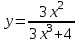
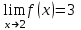 и
и 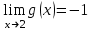 Определите, будут ли следующие функции непрерывными в точке 4:
Определите, будут ли следующие функции непрерывными в точке 4: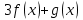 ;
;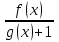
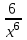 -4
-4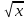
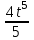 +8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 5;11 скорость движения точки будет наибольшей? Найдите величину этой скорости.
+8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 5;11 скорость движения точки будет наибольшей? Найдите величину этой скорости.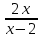 , проведённой через точку с абсциссой х0=1
, проведённой через точку с абсциссой х0=1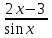 в точке x=
в точке x=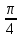 .
.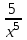 -6
-6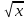
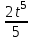 +8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 6;12 скорость движения точки будет наибольшей? Найдите величину этой скорости.
+8t3. ( S(t)- в метрах, t в секундах). В какой момент времени из отрезка 6;12 скорость движения точки будет наибольшей? Найдите величину этой скорости.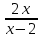 -3, проведённой через точку с абсциссой х0=1
-3, проведённой через точку с абсциссой х0=1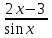 в точке x=
в точке x=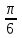 .
.

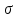 (x)
(x) 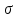 (x)
(x) 
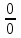 ,
, 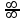 и при вычислении пределов
и при вычислении пределов