|
сор соч алгебра 10класс. сор соч алгебра 10 кл папка. Алгебра и начала анализа Суммативное оценивание за раздел Функция, ее свойства и график
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА»
Тема
|
Решение тригонометрических неравенств
|
Цели обучения
|
10.2.3.17. Уметь решать простейшие тригонометрические неравенства
10.2.3.18. Уметь решать тригонометрические неравенства
|
Критерии оценивания
|
Обучающийся:
Решает простейшие тригонометрические неравенства
Находит решение тригонометрических неравенств
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
Количество баллов
|
6
|
4
|
5
|
Всего баллов
|
15 баллов
|
1 ВАРИАНТ
Решите неравенство:
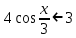
b ) 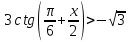
с)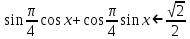
2. Определить, сколько целых решений имеет неравенство на интервале (0; 2).
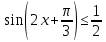
3. Решить квадратное тригонометрическое неравенство:
2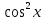 -3 -3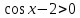
2 ВАРИАНТ
1.Решите неравенство:
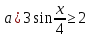
b) 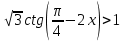
с)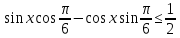
2. Определить, сколько целых решений имеет неравенство на интервале (0; 2).
2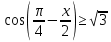
3.Решить квадратное тригонометрическое неравенство:
2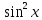 -3 -3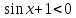
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Решает простейшие тригонометрические неравенства.
|
1а
|
использует формулу, тригонометрическую окружность;
|
1
|
находит решение неравенства;
|
1
|
1b
|
использует формулу тригонометрическую окружность;
|
1
|
выполняет преобразования и находит решение неравенства
|
1
|
1с
|
применяет формулу сумму и разности двух углов
|
1
|
выполняет преобразования и находит решение неравенства;
|
1
|
Определяет, сколько целых решений имеет неравенство на интервале
(0; 2).
|
2
|
использует формулу
|
1
|
Проверяет интервалы;
|
1
|
Находит решение простейших неравенств на каждом интервале
|
1
|
определяет целые решения исходного неравенства
|
1
|
Решить квадратное тригонометрическое неравенство.
|
3
|
Вводит новую переменную
|
1
|
Решает квадратное уравнение Находит корни
|
1
|
Применяет метод интервалов
|
1
|
Возвращается к замене и находит решение неравенства
|
1
|
|
|
Находит решение исходного неравенства
|
1
|
Всего баллов
|
15
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ ««ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА»
ФИ ОБУЧАЮЩЕГОСЯ_______________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Решает простейшие тригонометрические неравенства
|
Затрудняется в нахождении решения простейших тригонометрических неравенств
|
Допускает ошибки при решении простейших тригонометрических неравенств, содержащих синус / косинус / тангенс / котангенс
|
Pешает простейшие тригонометрические неравенства
|
Находит решение тригонометрических неравенств
|
Затрудняется в решении тригонометрических неравенств
|
Допускает ошибки при выполнении преобразований с помощью формул тригонометрии / нахождении общего решения
|
Решает тригонометрические неравенства
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «ВЕРОЯТНОСТЬ»
Тема
|
Элементы комбинаторики и их применение для нахождения вероятности событий. Условная вероятность. Правила сложения и умножения вероятностей. Формула Бернулли и ее следствия.
|
Цели обучения
|
10.3.1.4.Решать задачи на нахождение вероятностей, применяя формулы комбинаторики
10.3.2.8. Использовать формулу Бернулли и ее следствия при решении задач
10.3.2.4 Понимать и применять правила умножения вероятностей
* P(A ∙ B) = P(A) ∙ P(B)
* P(A ∙ B) = P(A) ∙ PA(B) = P(B) ∙ PB(A)
|
Критерии оценивания
|
Обучающийся
Применяет формулы комбинаторики при решении задач на нахождение вероятности
Применяет формулу Бернулли для решения задач на нахождение вероятностей
Применяет правило умножения вероятностей при решении задач
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
Количество баллов
|
3
|
3
|
4
|
Всего баллов
|
10 баллов
|
1 ВАРИАНТ
1.Сколькими способами из восьми человек можно избрать комиссию, состоящую из четырех членов?
2. На деревообрабатывающем комбинате 20% произведенных столярных изделий имеют дефект. При контроле качества продукции выявляется 60% дефектных изделий. Остальные столярные изделия поступают в продажу. Найдите вероятность того, что случайно выбранное при покупке изделие не имеет дефектов. Ответ округлите до сотых.
3. В коробке имеются 6 голубых и 8 розовых шаров.
1) Сколькими способами из коробки можно вынуть один шар любого цвета?
2) Сколькими способами из коробки можно вынуть два разноцветных шара?
2 ВАРИАНТ
1.Сколькими способами из девяти человек можно избрать комиссию, состоящую из шести членов?
2. На заводе 30% произведенных подшипников имеют дефект. При контроле качества продукции выявляется 65% дефектных подшипников. Остальные подшипники поступают в продажу. Найдите вероятность того, что случайно выбранный при покупке подшипник не имеет дефектов. Ответ округлите до сотых.
3. В ящике имеются 20 шаров: 8 зеленых и 12 желтых шаров.
1) Сколькими способами из коробки можно вынуть один шар любого цвета?
2) Сколькими способами из коробки можно вынуть два разноцветных шара?
Критерий оценивания
|
№ задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Применяет формулы комбинаторики при решении задач на нахождение вероятности
|
1
|
находит число возможных способов
|
1
|
использует формулу числа сочетаний;
|
1
|
выполняет вычисления
|
1
|
Применяет формулу Бернулли для решения задач на нахождения вероятностей
|
2
|
определяет все необходимые компоненты;
|
1
|
выполняет вычисления;
|
1
|
находит вероятность события (ответ обязательно должен быть округлен сотых)
|
1
|
Применяет правило умножения вероятностей при решении задач
|
3
|
находит число возможных способов вынуть шар одного цвета
|
1
|
использует формулу числа сочетаний
|
1
|
выполняет вычисления
|
1
|
находит произведение вероятностей двух зависимых событий
|
1
|
Общий балл
|
10
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ВЕРОЯТНОСТЬ»
ФИ ОБУЧАЮЩЕГОСЯ___________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Применяет формулы комбинаторики при решении задач на нахождение вероятности
|
Затрудняется в применении формул комбинаторики для решения задач на вероятность
|
Допускает ошибки в использовании правил произведения / суммы/ в вычислениях
|
Использует формулы комбинаторики при решении задач на нахождение вероятностей
|
Применяет формулу Бернулли для решения задач на нахождения вероятностей
|
Затрудняется в применении формулы Бернулли при решении задач
|
Допускает ошибки в применении формулы Бернулли/ошибки в вычислениях
|
Применяет формулу Бернулли для решения задач на нахождение вероятностей
|
Применяет правило умножения вероятностей при решении задач
|
Затрудняется в применении правил произведения вероятностей при решении задач
|
Допускает ошибки в использовании правила произведения независимых / зависимых событий при решении задач
|
Применяет правило произведения вероятностей при решении задач
|
СУММАТИВНОЕ ОЦЕНИВАНИЕ
ЗА РАЗДЕЛ «МНОГОЧЛЕН»
Тема
|
Общий вид многочлена с одной переменной. Деление «уголком» многочлена на многочлен. Теорема Безу, схема Горнера. Метод неопределенных коэффициентов
|
Цели обучения
|
10.2.1.3 Уметь распознавать многочлен с одной переменной и приводить его к стандартному виду;
10.2.1.4 Находить старший коэффициент, степень и свободный член многочлена с одной переменной;
10.2.1.13Знать метод неопределённых коэффициентов и применять его при разложении многочлена на множители;
10.2.1.8Применять теорему Безу и ее следствия при решении задач.
10.2.1.7Выполнять деление «уголком» многочлена на многочлен;
|
Критерии оценивания
|
Обучающийся:
Определяет многочлен с одной переменной и его элементы
Раскладывает многочлен на множители с помощью метода неопределенных коэффициентов
Применяет теорему Безу и ее следствия
Использует деление «уголком» для разложения многочленов на множители
|
Уровень мыслительных навыков
|
Применение
Навыки высокого порядка
|
Время выполнения
|
25 минут
|
ЗАДАНИЯ
Оценивание заданий работы
|
№ задания
|
1
|
2
|
3
|
4
|
Количество баллов
|
4
|
3
|
3
|
4
|
Всего баллов
|
14 баллов
|
1 ВАРИАНТ
Дано 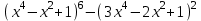 . Найдите . Найдите
а) степень многочлена;
б) старший коэффициент и свободный член;
в) сумму коэффициентов многочлена;
г) сумму коэффициентов при четных степенях.
Найдите значения А и В при которых данное тождество верное:
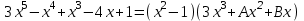
Многочлен 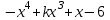 делится на двучлен делится на двучлен 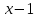 без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен 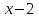
Используя деление «уголком», запишите в каноническом виде частное при делении многочлена 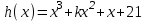 на двучлен на двучлен 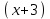 . Найдите все корни многочлена и разложите его на множители. . Найдите все корни многочлена и разложите его на множители.
2 ВАРИАНТ
Дано 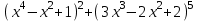 . Найдите . Найдите
а) степень многочлена;
б) старший коэффициент и свободный член;
в) сумму коэффициентов многочлена;
г) сумму коэффициентов при четных степенях.
Найдите значения А и В при которых данное тождество верное:
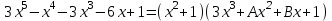
Многочлен 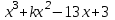 делится на двучлен делится на двучлен 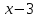 без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен 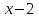 . .
Используя деление «уголком», запишите в каноническом виде частное при делении
Многочлена 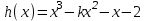 на двучлен на двучлен 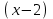 . Найдите все корни многочлена и разложите его на множители. . Найдите все корни многочлена и разложите его на множители.
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Определяет многочлен с одной переменной и его элементы
|
1
|
находит степень многочлена;
|
1
|
Находит старший коэффициент и свободный член;
|
1
|
Находит сумму коэффициентов многочлена;
|
1
|
Находит сумму коэффициентов при четных степенях;
|
1
|
Раскладывает многочлен на множители с помощью метода неопределенных коэффициентов
|
2
|
раскрывает скобки и приводит подобные слагаемые;
|
1
|
находит значение первой переменной;
|
1
|
находит значение второй переменной;
|
1
|
Применяет теорему Безу и ее следствия
|
3
|
использует теорему Безу;
|
1
|
находит значение параметра;
|
1
|
находит остаток;
|
1
|
Использует деление «уголком» для разложения многочленов на множители
|
4
|
делит многочлен на двучлен;
|
1
|
Записывает частное в каноническом виде;
|
1
|
находит корни квадратного трехчлена;
|
1
|
раскладывает многочлен на множители.
|
1
|
Итого
|
14
|
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «МНОГОЧЛЕНЫ»
ФИ ОБУЧАЮЩЕГОСЯ______________________________________________________
Критерий оценивания
|
Уровень учебных достижений
|
Низкий
|
Средний
|
Высокий
|
Определяет многочлен с одной переменной и его элементы
|
Затрудняется в определении многочлена с одной переменной и его элементов
|
Допускает ошибки при определении степени / старшего коэффициента / свободного члена / нахождении суммы коэффициентов многочлена с одной переменной
|
Oпределяет многочлен с одной переменной и указывает его элементы
|
Раскладывает многочлен на множители с помощью метода неопределенных коэффициентов
|
Затрудняется в применении метода неопределенных коэффициентов для разложения многочленов на множители
|
Допускает ошибки в применении метода неопределенных коэффициентов/ вычислительные ошибки при нахождении неизвестных
|
Применяет метод неопределенных коэффициентов для разложения многочленов на множители
|
Применяет теорему Безу и ее следствия
|
Затрудняется в применении теоремы Безу при решении задач
|
Допускает вычислительные ошибки при нахождении неизвестных
|
Применяет теорему Безу, при решении задач
|
Использует деление «уголком» для разложения многочленов на множители
|
Затрудняется в делении многочленов «уголком»
|
Допускает ошибки в делении «уголком» /вычислительные ошибки при разложении на множители
|
Делит многочлены «уголком» для разложения многочлена на множители
| |
|
|
 Скачать 0.87 Mb.
Скачать 0.87 Mb.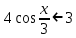
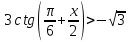
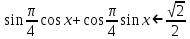
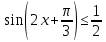
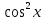 -3
-3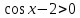
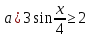
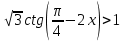
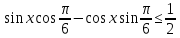
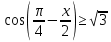
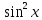 -3
-3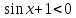
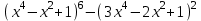 . Найдите
. Найдите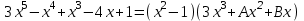
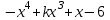 делится на двучлен
делится на двучлен 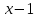 без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен
без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен 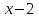
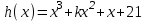 на двучлен
на двучлен 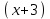 . Найдите все корни многочлена и разложите его на множители.
. Найдите все корни многочлена и разложите его на множители. 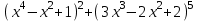 . Найдите
. Найдите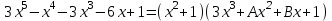
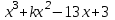 делится на двучлен
делится на двучлен 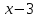 без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен
без остатка. Используя теорему Безу, найдите остаток при делении данного многочлена на двучлен 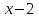 .
.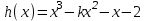 на двучлен
на двучлен 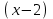 . Найдите все корни многочлена и разложите его на множители.
. Найдите все корни многочлена и разложите его на множители. 