МБА лекция. 06 Бизнес-курс МВА. Экономика и финансовые рынки. Финансовые рынки и денежная политика
 Скачать 5.53 Mb. Скачать 5.53 Mb.
|
|
Тема 6. Особенности оценки облигаций ОБЩИЕ ПРИНЦИПЫ И КЛЮЧЕВЫЕ ПОКАЗАТЕЛИ ОЦЕНКИ ОБЛИГАЦИЙ В большинстве случаев, выходя на рынок облигаций, инвестор сталкивается с уже сложившимся уровнем цен (исключение составляют случаи первичного размещения и ситуации, когда инвестор располагает столь значительными суммами, что способен влиять на рынок). Данный уровень цен задается рынком и является внешним параметром по отношению к инвестору. Уже на данном этапе мы сталкиваемся с показателем курса облигации, который представляет собой отношение рыночной цены к номиналу (в процентах). Если облигации продаются по цене ниже номинала, то говорят, что продажа производится с "дисконтом".Если облигации продаются по номиналу, а погашаются с начислением дополнительных процентов, то говорят, что облигации погашаются с премией. Однако то, что инвестор не может на данный уровень цен влиять, не означает, что инвестор может не задумываться о ценообразовании на рынке облигаций. Именно понимание того, как работает рынок облигаций, может защитить инвестора от ряда ошибок, а в некоторых случаях позволить ему заработать повышенный доход. Понимание процесса ценообразования несколько менее важно на развитых, эффективных рынках, поскольку в этом случае все равно невозможно найти недооцененные или переоцененные ценные бумаги. Однако российский инвестор должен быть крайне осторожен. Рынок корпоративных облигаций в настоящее время находится в стадии становления, и до входа его в развитую фазу неизбежно должно пройти определенное время. В течение этого времени рынок не будет соответствовать критериям эффективного рынка. А значит, инвестор должен будет самостоятельно тщательно оценивать инвестиционную привлекательность облигаций. Как формируется рыночная цена облигации? Как и цена любого товара, Цена облигации формируется под воздействием спроса и предложения со стороны инвесторов. При этом, однако, цена облигации не является случайной, а колеблется около своего естественного значения, т. н. внутренней стоимости (intrinsic value). Именно эта стоимость и будет интересовать нас в ближайшее время. Условимся, что в дальнейшем тексте цена облигации и купонные платежи, если не сказано иное, указываются в процентах от номинала (номинал облигации соответственно указывается как 100). Рассмотрим облигацию, имеющую срок обращения Т. С точки зрения инвестора облигация является обещанием эмитента уплачивать инвестору определенные суммы денег (С1, С2, ..., Сt) в определенные моменты времени (t1, t2, ..., tT). Таким образом, обещанный денежный поток по облигации описывается следующим образом:
Для облигации с постоянным купоном С1=С2=С3=Сt–1=С – купонные платежи, а в платеж Сt включен также возврат номинальной стоимости облигации (100), т. е. Сt = С + 100. Купонные платежи обычно выплачиваются с регулярным интервалом, для простоты мы будем считать его равным одному году (в дальнейшем мы отдельно рассмотрим оценку облигаций с купонным периодом, меньшим одного года), кроме того, для простоты мы будем считать, что первый купон также будет выплачен через один год, начиная с текущего момента, т. е. t1=1, t2=2, tT=T (такая ситуация означает, что мы покупаем облигацию либо при ее первичном размещении, либо в дату выплаты очередного купона). Таким образом, для рассматриваемых нами облигаций денежный поток будет иметь следующий вид:
При определении того, какой должна быть цена облигации, инвестор должен дисконтировать ожидаемые платежи и просуммировать их, т. е. вычислить чистую текущую стоимость (обычно обозначается как NPV – Net Present Value) потока платежей по облигации. Если платежи происходят регулярно с периодичностью раз в год, то: Для облигации с постоянным периодическим купоном эта формула имеет следующий вид: При этом инвестор должен выбрать соответствующую норму дисконтирования rс учетом своих инвестиционных предпочтений и воспринимаемого риска. Определение требуемой нормы дисконтирования и является самым сложным моментом в ценообразовании облигаций, подробно этот вопрос будет рассмотрен ниже. Пример: Предприятие ABC выпустило облигации с купонным платежом 10% сроком на 3 года. Требуемая инвестором норма доходности по данным облигациям составляет 5%. Тогда NPV ожидаемых поступлений по данной облигации и соответственно цена облигации составят: Строго говоря, данный подход не вполне правилен, поскольку облигация представляет собой обязательство уплатить определенные суммы, но не означает, что эти суммы действительно будут уплачены. Поэтому более корректно было бы вычислять так называемую ожидаемую NPV, которая определяется как дисконтированная стоимость ожидаемых значений будущих поступлений. Обозначив ожидаемую NPV как E(NPV), имеем следующую формулу для ее вычисления: где: р1, р2, рТ – вероятности того, что соответствующие платежи будут произведены. Ожидаемая NPV всегда меньше обещанной NPV и совпадает с ней только для абсолютно надежных облигаций, вероятность выплат по которым равна 1. Пример: Рассмотрим то же самое предприятие ABC, которое выпустило облигации с купонным платежом 10% сроком на 3 года. Предприятие может обанкротиться, вероятность банкротства равна 2% в каждый год. В случае наступления банкротства никаких дальнейших платежей по облигациям произведено не будет. Тогда ожидаемые платежи по облигации будут иметь вид:
Пусть требуемая норма доходности составляет 5%. Тогда NPV = –113,62 Ожидаемая NPV = –107,48 Однако вычисление ожидаемой NPV требует знания вероятности неплатежа, что обычно нереально. Более того, на практике могут встречаться задержки платежей или частичные платежи, что еще сильнее усложняет применение концепции ожидаемой NPV. Поэтому подход, связанный с расчетом ожидаемой NPV, освещается в основном только в теории. На практике возможность неплатежа учитывается при выборе коэффициента дисконтирования. Хорошо известно, что облигации надежных компаний могут стоить гораздо дороже, чем облигации компаний, чья платежеспособность вызывает сомнения. Происходит это как раз потому, что при оценке их стоимости используются разные коэффициенты дисконтирования. ДОХОДНОСТЬ ОБЛИГАЦИЙ С понятием NPV тесно связано понятие внутренней нормы доходности. Внутренняя норма доходности (обычно обозначается как IRR – Internal Rate of Return) – это такой коэффициент дисконтирования, при котором чистая текущая стоимость денежного потока равняется нулю. Применительно к облигациям внутренняя норма доходности – это такая процентная ставка, при которой дисконтированная стоимость будущих доходов по облигации равна ее текущей цене. Этот показатель принято называть доходностью к погашению. В соответствии с описанным различием между обещанной и ожидаемой NPV надо различать также так называемую обещанную доходность к погашению и ожидаемую доходность к погашению. Обещанная доходность к погашению – это такой коэффициент дисконтирования, при котором обещанная NPV равняется нулю. Ожидаемая доходность к погашению – это такая доходность к погашению, при которой нулю равняется ожидаемая NPV. Вернемся к примеру с облигациями ABC. Пусть их текущая цена равняется номиналу, то есть –100. Обещанная доходность к погашению составляет IRR (-100,10,10,110)= 10% Ожидаемая доходность к погашению составляет IRR (-100;9,8;9,6;103,53) = 7,8% Приведенные выше примеры рассматривали конкретного инвестора и формирование его оценки облигаций. Рыночная цена облигации формируется с учетом оценок множества инвесторов, фактически формирование такой цены не отличается от формирования цены любого другого товара. В результате цена облигации определяется тем, какая норма доходности требуется рынком по соответствующей облигации. При изменении требуемой нормы доходности цена облигации меняется в противоположном направлении. Чем выше требуемая норма доходности, тем ниже рыночная цена облигации, и наоборот. Графически эта взаимосвязь имеет следующий вид (диаг. 1): 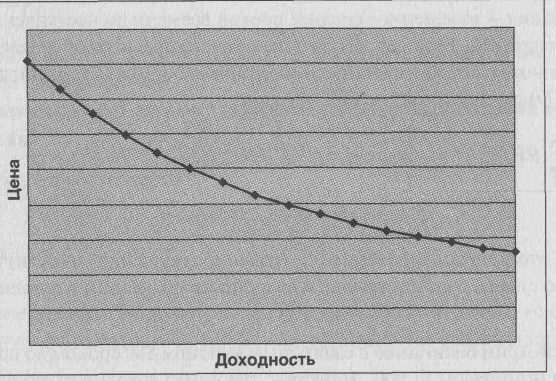 Диаграмма 1. Взаимосвязь цены и доходности Для обычной облигации с ежегодными платежами (переменными, но заранее известными) формула взаимосвязи цены и доходности имеет уже знакомый нам вид: Для дисконтной облигации вид этой зависимости проще, а именно: Зависимость между ценой и доходностью является нелинейной (это видно из приведенного выше графика). Эту нелинейность необходимо учитывать при проведении точных расчетов. Однако при этом было бы исключительно удобно иметь некую меру, выраженную конкретным числом, которая отражала бы степень взаимосвязи между ценой и доходностью. Известно, что в большинстве случаев чем больше срок облигации до погашения, тем чувствительнее ее цена реагирует на изменение процентных ставок. Однако срок до погашения облигации не является полностью корректной мерой такой чувствительности. В качестве такой меры используется дюрация облигации. Понятие дюрации Дюрация – взвешенное среднее сроков времени до наступления оставшихся платежей. Веса в формуле взвешенного среднего определяются как доля данного платежа в стоимости облигации. Формула для вычисления дюрации (D) выглядит следующим образом: 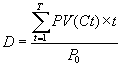 При этом дисконтирование (вычисление текущей стоимости) производится по ставке, соответствующей доходности облигации к погашению. Пример: Рассмотрим облигацию с ежегодным купоном –80 сроком до погашения 3 года и номиналом –1000. Допустим, требуемая доходность такой облигации составляет 10% годовых, соответственно ее цена равняется –950,25. Какова дюрация такой облигации?
Дюрация = 2639,17/950,25 = 2,78 года. Дюрация связана со сроком до погашения облигации, но зависит также от купонных платежей. По дисконтным облигациям (с нулевым купонным платежом) дюрация равна сроку обращения облигации. По купонным облигациям дюрация всегда меньше срока обращения, причем чем выше ставка купона, тем ниже дюрация. Важно подчеркнуть, что дюрация зависит также от того, какова требуемая норма доходности по облигациям. Дюрация очень важна как мера чувствительности цены облигации к изменениям уровня процентных ставок. При этом в качестве меры чувствительности цены облигации к изменению процентной ставки обычно применяется так называемая модифицированная дюрация, которая вычисляется следующим образом: Математически взаимосвязь между изменением цены облигации и дюрацией имеет следующий вид. Изменение цены (в %) =–DM × Изменение доходности облигаций в процентных пунктах. Или, применяя обозначения: Фактически модифицированная дюрация – это не что иное, как первая производная функции зависимости цены облигации от ее доходности. Пример: Рассмотрим ту же самую облигацию. Допустим, что требуемая норма доходности возросла до 11% годовых. Как изменится цена облигации? Вычислим модифицированную дюрацию. Она составит 2,78/1,1 = 2,53 Согласно приведенной формуле процентное изменение цены облигации можно вычислить следующим образом. Изменение доходности составляет 1-процентный пункт, соответственно dг=1%. Тогда процентное изменение цены составит –2,53 × 1% = –2,53%. Т. е. цена облигации должна будет упасть примерно до –926,27. В реальности дюрация выражает лишь приближенное изменение цены. Точное значение цены в нашем случае должно было бы составить –926,69. Чем больше дюрация, тем соответственно больше реагирует цена облигации на изменения процентных ставок. Причем дюрация более точно выражает степень зависимости цены облигации от процентных ставок, чем ее срок до погашения. ПРЕМИЯ И ДИСКОНТ По купонным облигациям, если требуемая норма доходности ниже купонной ставки, облигация продается по цене выше номинала. Тогда говорят, что облигация продается с премией. Если требуемая доходность выше купонной ставки, цена облигации сложится ниже номинала, облигация будет продаваться с дисконтом. По мере сокращения срока до погашения величина премии или дисконта также уменьшается, причем все более быстрыми темпами. Пример: Рассмотрим 5-летнюю облигацию с купонным доходом 10% и требуемой доходностью 8% годовых. Тогда цена такой облигации составит: Р = 10/1,08 + 10/1,082 + 10/1,083 + 10/1,084 + 110/1,085 = 108, т. е. облигация будет торговаться выше номинала с премией, равной 8. Рассмотрим теперь аналогичную облигацию с требуемой нормой доходности, равной 12%. Цена такой облигации составит: Р = 10/1,12 + 10/1,122 + 10/1,123 + 10/1,124 + 110/1,125 = 92,8, т. е. облигация будет торговаться ниже номинала с дисконтом, равным 7,2. Теперь предположим, что прошло 2 года и требуемая доходность осталась 12%. Тогда цена облигации составит: Р= 10/1,12 + 10/1,122 + 110/1,123 = 95,2, т. е. дисконт по облигации снизился с 7,2 до 4,8. 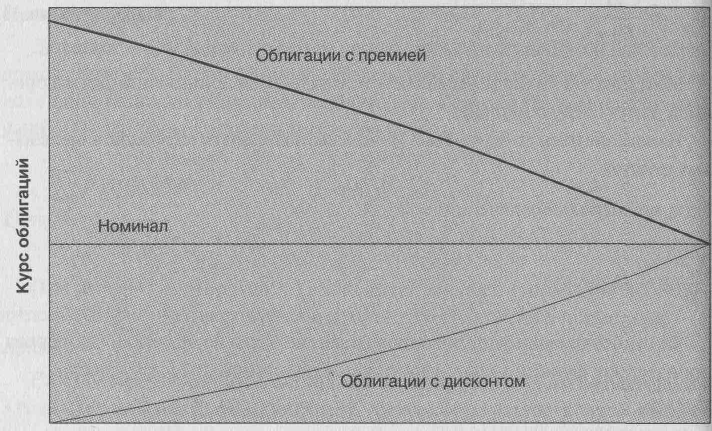 Диаграмма 2. Премия и дисконт в цене облигации |
