МБА лекция. 06 Бизнес-курс МВА. Экономика и финансовые рынки. Финансовые рынки и денежная политика
 Скачать 5.53 Mb. Скачать 5.53 Mb.
|
|
Учет накопленного купонного дохода. Расчет доходностей облигаций, предусматривающих выплату купона чаще одного раза в год. Выше мы исходили из предположения о том, что выплата купона по облигациям осуществляется 1 раз в год и покупка облигации осуществляется в дату первичного размещения или в дату выплаты очередного купона. Что происходит, если покупка облигации происходит в момент, когда с даты выплаты последнего купона уже прошло определенное время. Очевидно, что в этом случае за истекший период по облигациям накопился некий доход, называющийся накопленным купонным доходом – НКД. НКД равен размеру купона, умноженному на долю прошедшего купонного периода. Например, если ежегодный купон составляет 12% годовых и с даты выплаты последнего купона прошло 3 мес., то НКД составит 12% × 1/4 = 3%. По традиции при сделках с облигациями указывается т. н. чистая цена, не учитывающая НКД. Однако при реальных расчетах продавец облигации уплачивает покупателю НКД. Пример: Рассмотрим облигации ОАО "РИТЭК"1-го выпуска.1 октября 2001 года по ним была осуществлена выплата купона. Следующий купон должен быть уплачен 1 февраля 2002 года, ставка купона – 14,15% годовых. Какова величина НКД на 19 октября 2001 года? С момента выплаты последнего купона прошло 18 дней. Общая величина купонного периода составляет 123 дня. Соответственно прошло 18/123 = 0,146 купонного периода. Общий доход за купонный период составит 14,15 × 123/365 = 4,768%. Таким образом, НКД = 0,146 × 4,768 = 0,698%. При покупке облигаций покупатель должен выплатить продавцу эту величину дополнительно к указанной в торговой системе цене облигации. Теперь рассмотрим, как считать доходность по облигациям, предусматривающим выплату купона чаще, чем раз в год. Например, в мировой практике часто применяется полугодовая выплата купона. Очевидно, базовое уравнение для расчета доходности будет точно таким же, только годовой период заменится полугодовым. Формула для расчета цены будет иметь следующий вид: Итак, мы рассмотрели основные показатели, используемые при оценке облигаций: курс облигации, доходность, дюрация, накопленный купонный доход. Теперь перейдем непосредственно к методам оценки. Применение метода капитализации дохода к оценке корпоративных облигаций. Принимая решение об инвестировании средств в долговые ценные бумаги, инвестор вынужден сопоставлять расходы, которые он должен осуществлять в настоящее время, с ожидаемыми результатами, т.е. доходами. Аналогичные инвестиционные решения при выпуске ценных бумаг с фиксированной доходностью принимает эмитент, постоянно определяя стоимость обслуживания привлекаемого финансирования. Все расчеты строятся на алгоритмах финансовых вычислений по долговым ценным бумагам. Владельцев облигаций в основном интересуют два показателя эффективности: доходность и курс облигаций. Оцениваемые наряду с ожидаемыми рыночными процентными ставками и чисто техническими параметрами выпуска, показатели дают информацию для принятия разумных решений и выработки надежных инвестиционных стратегий. Как и большинство ценных бумаг, облигация может приносить доход двумя способами. Во-первых, в форме процентной ставки (купона) по займу, которая в большинстве случаев представляет собой фиксированную годовую величину. Доходы по купонам выплачиваются несколько раз в год. Во-вторых, можно достичь прироста капитала, который представляет собой разницу между ценой, уплаченной за облигацию, и ценой, по которой инвестор продает облигацию, что может представлять собой сумму к погашению по датированной облигации. Анализируя доходность облигации, следует понимать, что процентные ставки (основной определяющий фактор для оценки облигаций) и цены облигаций меняются в противоположных направлениях. Следовательно, можно сказать, что цены облигаций растут при ожидаемом падении процентных ставок, и цены облигаций снижаются при ожидаемом росте процентных ставок. Следующей важной чертой, как уже говорилось, является влияние уровня инфляции. Если уровень инфляции высок, то это снизит покупательную способность в будущем, т.е. на момент погашения займа на полученные деньги нельзя будет купить такое же количество товаров и услуг, как сейчас. Однако если существует уверенность участников рынка, что увеличение процентных ставок остановит инфляцию, то, несмотря на приведенное выше утверждение, по которому цены облигаций должны упасть, цены облигаций могут остаться неизменными или даже начать расти. Хотя это правило и верно в большинстве случаев, однако оно не является абсолютной гарантией. Облигации могут быть выпущены с одной или несколькими датами погашения. Для того чтобы оценить полный доход, необходимо понимать последствия использования облигаций с различными характеристиками. Если по облигации существует только одна дата погашения, то именно эта дата будет использоваться для расчета дохода. Однако если по облигации существует, например, две даты погашения с разницей в два года, то необходимо определить, какая из этих дат имеет большую вероятность. Один из способов определения наиболее вероятной даты погашения заключается в том, чтобы посмотреть, является ли текущая цена облигации выше или ниже номинала. Если цена выше номинала (т.е. процентные ставки в настоящий момент ниже, чем при выпуске облигации), то это может означать, что эмитент в настоящий момент может заимствовать деньги по более низкой ставке, чем он платит сейчас. Следовательно, эмитент постарается погасить облигацию на самую раннюю дату, и первая дата погашения будет использоваться в расчетах дохода. С другой стороны, если цена меньше номинала (т.е. процентные ставки выросли), то в интересах заемщика продержать эти облигации как можно дольше. Соответственно в расчетах будет использоваться наиболее поздняя дата. Облигации являются важным объектом финансовых инвестиций. С момента их эмиссии и до погашения они продаются и покупаются по установившимся на рынке ценам. Рыночная цена в момент эмиссии может быть ниже номинала, равна номиналу и выше номинала. Поскольку номиналы у разных облигаций существенно различаются между собой, то часто возникает необходимость в сопоставимом измерителе рыночных цен облигаций. Таким показателем является курс. Под курсом облигации (Рt)понимают покупную цену одной облигации в расчете на 100 единиц номинала (в денежном выражении): где St – текущая рыночная цена; М – номинальная стоимость. На зарубежном рынке капитала термин "цена облигации" часто означает ее курс. Рыночная цена и курс зависят от уровня доходности облигации, уровня ссудного процента в момент оценки и ряда других условий, важнейшим из которых является оценка надежности инвестирования. Как уже было отмечено, доход от облигации складывается из нескольких элементов: купонного дохода или начисления процентов; изменения стоимости ценной бумаги (приближение ее к выкупной цене) за соответствующий период времени; если облигация была куплена с дисконтом, то этот элемент – положительная величина; если же она куплена с премией, то это отрицательная величина; наконец, если облигация куплена по номиналу, то этот элемент отсутствует. На практике весьма часто возникает необходимость определения фактической доходности инвестиций при известном курсе облигации или цене ее реализации. Иначе говоря, надо определить финансовую эффективность займа. Подобного рода задача может возникнуть при выборе одного из различных условий предлагаемых займов, условий получения кредита и т.д. Определение доходности является ориентиром эффективности измерения облигаций на финансовом рынке заемных капиталов. Показатель текущей доходности является простейшей мерой, которая характеризуется текущие поступления за год относительно сделанных инвестиций. Доходность является единственным наиболее важным критерием на рынке облигаций и служит множеству целей. Этот критерий предназначен для отслеживания состояния рынка, а также для определения дохода на вложенный капитал от одного выпуска. Инвестор, вкладывающий деньги в облигации, должен определить доход, который ему приносит купон в денежном выражении. Это можно сделать, рассматривая купон как часть текущей цены. Используется именно текущая цена, а не та цена, которая была уплачена за облигацию инвестором. После необходимо решить: оставить эту облигацию или продать и использовать вырученные средства для вложения в другие инвестиции. Реальное сравнение можно провести только с доходами, получаемыми в настоящий момент по другим инвестициям. Текущая доходность облигации отражает отношение годовой прибыли к текущей рыночной цене: где М – номинальная стоимость облигации, St– текущая рыночная цена, g– купонная ставка процента. Доход, полученный за все время владения облигацией, складывается из купонных выплат и цены погашения облигации, выплачиваемой в конце срока владения. Обозначим через С1, С2, С3,..., Сtвсе денежные доходы, полученные владельцем в течение владения облигацией. Сюда относятся выплаты по купонам и цена погашения облигации. Тогда современная (рыночная) стоимость облигации (Р)равна сумме всех дисконтированных доходов: где r – доходность облигации (ставка помещения), или ставка дисконтирования. Соотношение связывает рыночную цену облигации с доходностью к погашению или со ставкой дисконтирования. Если будущие доходы (С1, С2, С3,..., Сt) известны, то соотношение связывает между собой две переменные – доходность (r) и цену облигации (Р). Формула позволяет решать две основные задачи: а) определять цену облигации, если известна доходность (ставка дисконтирования); б) определять доходность облигации, если известна ее цена. Очевидно, что эти две задачи являются обратными друг другу. Как видно из формулы, если будущие доходы по облигации фиксированы, то ставка доходности облигации тем ниже, чем выше цена. Облигации продаются и покупаются по текущим ценам, а не по номинальной стоимости, которая на практике выполняет только две функции. Во-первых, обычно это сумма, которая выплачивает при погашении, а во-вторых, это та сумма, на основе которой рассчитывается купон. Инвестор при выборе объекта инвестирования в облигации руководствуется следующими параметрами выпуска: надежность и обеспеченность инвестирования в облигацию, доходность к погашению, финансовое положение эмитента, купонный годовой доход, динамика рыночной стоимости облигации, срок долгового обязательства, условия выкупа и отзыва, ликвидность на вторичном рынке, статус эмитента, рейтинг облигационного выпуска. Инвестирование в облигации защищено от риска, так как облигации – это долговые обязательства, поэтому при банкротстве эмитента, выплаты держателям облигации производятся в первую очередь. Одной из характеристик, определяющих бескупонные (дисконтные) облигации, являются облигации, приносящие их владельцу доход только в том случае, если они куплены по цене ниже номинала. Для облигаций такого типа устанавливается дата погашения и номинал. Купонный доход не начисляется и не выплачивается. Поэтому такие облигации называются бескупонными или облигациями с нулевым купоном, а также дисконтными. Поскольку происходит только одна выплата – погашение номинала N,то цена облигации определяется как: где T – время владения облигацией (в годах) до ее погашения. Курс облигации (K)определяется соотношением: Если известна цена бескупонной облигации или ее курс, то доходность облигации к погашению (r) равна 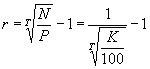 Если срок облигации меньше года или величины рыночных ставок невелики, доходность облигации (r)определяют по простой процентной ставке: По облигациям с выплатой процентов и номинала в конце срока математические расчеты ведут по сложной процентной ставке g,и текущие выплаты купонного дохода не производятся; накопленный купонный доход выплачивается в момент погашения вместе с номинальной стоимостью. Таким образом, владелец облигации в конце срока получает сумму, равную N × (1 + g)×T.Если T – срок владения облигацией (в годах, T – не обязательно целое число лет), то цена облигации (Р)и ее курс (K)связаны с доходностью к погашению следующими соотношениями: Доходность облигаций (r) с выплатой процентов и номинала в конце срока равна 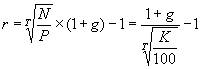 Когда доход по облигациям складывается из периодических купонных выплат и выплаты номинальной стоимости в конце срока, то они называются облигациями с фиксированным купоном. Доходы по купонам выплачиваются, несколько раз в году. Таким образом, текущая стоимость облигации с фиксированным купоном складывается из текущей стоимости аннуитета и текущей стоимости номинала. Если выплаты купонов происходят ежегодно, то рыночная цена облигации (Р) равна 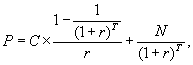 где: С – годовой купонный доход (в рублях), N – номинал облигации (в рублях), T – срок облигации (в годах), r – доходность к погашению или ставка дисконтирования. Курс облигации (K)(при ежегодной выплате купонного дохода) определяется выражением: 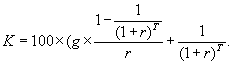 Соотношения рыночной цены и курса связывают стоимость облигации или курс с доходностью к погашению. Если известна доходность z, то курс можно определить с помощью соотношения. Укажем на следующие особенности облигаций с постоянным купоном. Если облигация приобретена по номиналу (по курсу 100), то доходность к погашению r равна ставке купонного дохода g.Если облигация приобретена с дисконтом (по курсу меньше 100), то доходность к погашению больше ставки купонного дохода (r > g).Если же облигация приобретена с премией (K > 100), то доходность к погашению меньше ставки купонного дохода (r < g). В последнем случае (при покупке с премией), владелец облигации также может получить доход, если не произойдет досрочного выкупа облигации эмитентом. Если купонные выплаты происходят несколько раз в году, то часто для финансовых расчетов используется номинальная процентная ставка доходности; при условии начисления процентов траз в году (т – количество выплат купонного дохода в году). Стоимость облигации с фиксированным доходом связана с номинальной ставкой доходности соотношением: 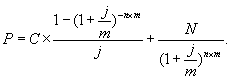 Заметим, что если годовой купонный доход равен С, авыплаты происходят траз в году, то каждый раз выплачивается сумма, равная С/т. Часто используют простую процентную ставку доходности для облигаций с фиксированным купоном. Напомним, что при начислении дохода по простой процентной ставке, доход каждый раз начисляется на первоначальную сумму, то есть предполагается, что доходы по процентам не реинвестируются. Поэтому можно записать: 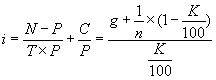 Более сложные математические вычисления определяют факторы ликвидности облигации с переменным (неизвестным) купонным доходом. Они дают его владельцам право на периодическое получение процентного (купонного) дохода. При этом возможно получение дисконта, если цена приобретения облигаций (при первичном размещении или на вторичных торгах) будет меньше цены их реализации, в том числе при погашении облигаций по их номиналу. В случае с государственными ОФЗ-ПК размеры каждого купона объявляются непосредственно перед началом соответствующего купонного периода, исходя из текущей доходности выпусков ГКО, которые погашаются примерно в одно время с датой выплаты этого купона. Общая формула доходности и величина накопленного купонного дохода определяется аналогично облигациям с известным купонным доходом. Для определения доходности используются оценки неизвестных купонов. При этом предполагается, что все неизвестные купоны равны между собой. При этом доходность (доходность к погашению) рассчитывается по формуле сложных процентов, и в случае применения к облигациям с переменным купонным доходом выглядит следующим образом: 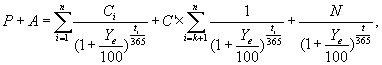 где: Ye– эффективная доходность к погашению (в процентах, с точностью до сотых процента), которая определяется из приведенной выше формулы численными методами; N– номинал облигации (руб.); Р– цена облигации (руб.); А– величина накопленного купонного дохода (руб.); С– размер T-того купона (руб.); n – количество предстоящих выплат купона; ti – число дней до выплаты соответствующего купона; t – срок до погашения облигации (в днях). Как правило, t = tn; k – количество ближайших известных купонов; С' – оценка неизвестных купонов, полученная по той же методике, по которой определяется размер купона. При осуществлении оценки облигаций с переменным купонным доходом особое внимание уделяется расчету фактора дюрации (дюрация Макколи). Данная характеристика является критерием измерения (в годах) чувствительности цен облигаций к сроку действия облигации и размеру купона. В сущности, это показывает влияние купона на срок действия облигации. Облигация без купона будет иметь дюрацию, равную сроку действия облигации, но чем выше купон, тем меньше будет дюрация по отношению к сроку погашения. Дюрация является качественной и количественной характеристикой рисков, связанных с владением облигацией. Чем меньше дюрация, тем быстрее отдача от облигации и тем меньше риск неполучения доходов. Кроме того, чем больше срок облигации, тем больше дюрация, и наоборот. Также, чем больше ставка помещения, тем меньше дюрация. Фактически дюрация не что иное как первая производная функции зависимости цены облигации от ее доходности. Дюрация рассчитывается как средневзвешенный срок погашения облигации, и весами здесь выступают дисконтированные денежные потоки за каждый период. Таким образом, больше веса дается более отдаленным по времени денежным потокам, так как на них в большей степени воздействуют изменения процентных ставок. Как уже говорилось, облигация с более высоким купоном имеет меньшую дюрацию. Это дает возможность увидеть, что такая облигация менее чувствительна к изменениям процентных ставок. На данном этапе рассмотрения доходного подхода к оценке облигаций мы вплотную к рискам, связанным с различными факторами, действующими на облигацию. Сразу отметим, что в рассмотрении рисков по корпоративных облигациям акцент сделан на их учет при оценке. Риски по корпоративным облигациям, механизм их индексации Как было отмечено выше, основной постулат теории принятия инвестиционных решений состоит в том, что все инвестиционные инструменты обладают двумя важнейшими характеристиками: доходом и риском. При этом чем выше риск, тем больше должен быть доход, и наоборот. Ожидаемая норма отдачи по рисковым вложениям (Rexp)должна превышать норму отдачи по безрисковым вложениям (Rrf) на величину определенной премии за риск (RP), т. е. Rexp = Rrf + RP Однако как уже указывалось, в практике рынка облигаций используется не ожидаемая, а обещанная доходность (R), которая равняется ожидаемой доходности плюс премия за возможность неплатежа (DP). Тогда обещанная доходность может быть представлена как сумма следующих компонент: R=Rrf + DP + RP Факторами риска по облигациям являются следующие: риск неопределенности платежей, риск низкой ликвидности, срок до погашения. Тогда можно представить требуемую обещанную доходность по облигациям в виде следующей суммы: |
