Физика твердого тела (тексты лекций). Гомельский государственный университет имени Франциска Скорины С. А. Хахомов, А. В. Семченко, Ю. В. Никитюк физика твердого тела
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
2.3.2 Плотность упаковки2.3.3 Координационное число2.4 Анизотропия кристаллов 2.1 Кристаллические и аморфные тела Всякое жидкое вещество при охлаждении теряет свойство текучести и переходит в твердое состояние. Однако процесс перехода из жидкого состояния в твердое для разных веществ не одинаков. Известны два различных вида затвердевания. 1. Кристаллизация вещества. В этом случае в жидкости, охлажденной до определенной температуры, появляются мельчайшие кристаллики (области упорядоченно расположенных и прочно связанных между собою частиц (молекул, атомов или ионов) - центры кристаллизации, которые при дальнейшем отводе тепла от вещества разрастаются за счет присоединения к ним частиц из жидкой фазы и охватывают весь объем вещества. 2. Затвердевание вследствие сравнительно быстрого повышения вязкости жидкости с понижением температуры. Известны две разновидности этого процесса. У некоторых веществ (сургуч, воск, смола) кристаллизация совсем не наблюдается: они называются аморфными телами. Другие вещества, например, стекло, способны кристаллизоваться, но вязкость у них быстро возрастает с понижением температуры. Последнее затрудняет перемещение молекул, необходимое для формирования и роста кристаллов и, таким образом, вещество успевает затвердевать до наступления кристаллизации. Такие вещества называются стеклообразными. Процесс кристаллизации этих веществ очень медленно протекает в твердом состоянии, причем легче при более высокой температуре. Известно, например, явление «расстекловывания» стекла. Оно обусловлено образованием внутри стекла мелких кристалликов, на границах которых происходит отражение и рассеяние света, вследствие чего стекло теряет прозрачность. Аналогичная картина наблюдается при «засахаривании» прозрачного сахарного «леденца». Иногда одно и то же вещество может затвердеть как в кристаллической, так и в аморфно-стеклообразной форме. Стеклообразные тела тоже относятся к разряду аморфных тел, так как они не имеют кристаллической структуры. Аморфные тела можно рассматривать как жидкости с очень высоким коэффициентом вязкости. Оказывается, что у аморфных тел можно наблюдать слабо выраженное свойство текучести. Если, например, наполнить воронку кусками воска или сургуча, то через некоторое время (разное для разных температур) куски аморфного тела будут постепенно расплываться, принимать форму воронки и «вытекать» из нее в виде стержня. Даже у стекла обнаружено свойство текучести. Измерения толщины оконных стекол в старых зданиях показали, что за несколько веков стекло успело стечь сверху вниз, так что нижняя часть стекла оказалась немного толще, чем верхняя. Поэтому, строго говоря, твердыми телами следует называть только кристаллические тела. Аморфные же тела по некоторым свойствам и главным образом по строению больше подходят на жидкости: их можно рассматривать как сильно переохлаждённые жидкости, обладающие очень высокой вязкостью. В чем же основное различие между кристаллическими и аморфными телами? Рассмотрим этот вопрос сначала с энергетической стороны. Если наблюдать процесс плавления и затвердевания кристаллических и аморфных тел, то можно заметить, что кристаллические тела имеют точку плавления, при которой вещество находится в устойчивом состоянии в обеих фазах - в твердой и в жидкой. Аморфные же тела, постепенно размягчаясь при нагревании, не имеют определенной температуры, соответствующей переходу твердой фазы в жидкую. Графически это изображено на рисунке 2.1. Участок ВС графика соответствует процессу плавления кристаллического тела. Количество тепла, получаемого нагреваемыми телами от нагревателя за единицу времени, можно приблизительно считать постоянным. Однако на участке ВС температура тела не изменяется, хотя тепло от нагревателя к нему по-прежнему подводится. Теплота расходуется на процесс плавления. При температуре плавления молекулы твердого тела получают возможность оторваться от поверхности кристалла и перейти в жидкую фазу. Но при этом переходе они приобретают большую свободу движения: появляется возможность поступательного движения молекул внутри жидкой фазы. Значит, чтобы оторваться от поверхности кристалла и перейти в жидкое состояние, молекула должна получить определенное количество энергии. Таким образом, единица массы вещества, находящегося при температуре плавления, в жидкой фазе будет обладать более высокой внутренней энергией, чем единица массы того же вещества в кристаллической фазе при этой же температуре. Разность этих внутренних энергий будет равна удельной теплоте плавления. Обратный процесс может происходить только в случае, если от системы «жидкая фаза - кристалл» отводится энергия, так как при кристаллизации выделяется такое же количество тепла, какое было поглощено при плавлении данного кристаллического тела. На графике для аморфных тел нет горизонтального участка, а наблюдается лишь точка перегиба Е. Температуру, соответствующую этой точке, условно называют температурой размягчения аморфного тела. Вообще же у аморфных тел при повышении температуры размягчение происходит постепенно до состояния очень вязкой жидкости. При дальнейшем повышении температуры вязкость жидкости уменьшается. Удельная теплота плавления у аморфных тел отсутствует; подвод тепла сопровождается плавным повышением температуры, постепенным увеличением энергии теплового движения молекул, что соответствует увеличению текучести жидкости и уменьшению ее вязкости. О 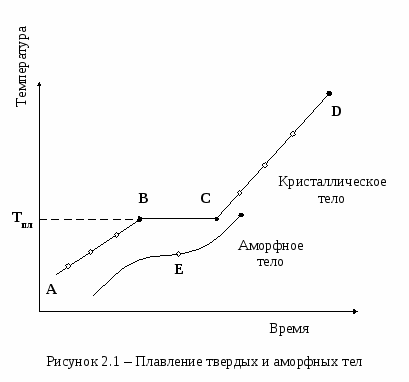 шибочным является представление, что переход вещества из жидкого состояния в твердое означает сближение молекул, которое сопровождается увеличением сил сцепления между ними, а это и создает «твердость» вещества. Дело в том, что некоторые вещества (вода, висмут, сурьма) при кристаллизации увеличиваются в объеме, следовательно, средние расстояния между соседними молекулами у этих веществ будут в твердой фазе больше, чем в жидкой, хотя, безусловно, в твердой фазе молекулы будут прочнее связаны между собой. Исходя из этого можно утверждать, что решающим фактором в процессе отвердевания кристаллических тел является не уменьшение расстояния между соседними частицами, а ограничение свободы их теплового движения. Само же это ограничение обусловлено увеличением сил связи между частицами, которое возникает при упорядоченном расположении их в кристалле. О том, что при кристаллизации происходит упорядоченное расположение молекул в кристалле, свидетельствует явление переохлаждениянекоторых жидкостей. У аморфных тел состояние переохлаждения не наблюдается. Это значит, что нельзя, охладив аморфное тело значительно ниже температуры размягчения, сохранить у него достаточно низкую вязкость, соответствующую жидкому состоянию. Таким образом, с энергетической стороны имеет место принципиальное различие между кристаллическими и аморфными телами, заключающееся в том, что процесс плавления и затвердевания кристаллических тел сопровождается определенным тепловым эффектом. У аморфных тел этого теплового эффекта нет. Различие между аморфными и кристаллическими телами не ограничивается только особенностью перехода из жидкого состояния в твердое. Одной из основных особенностей кристаллических тел является анизотропиясвойств. Поскольку анизотропия физических свойств кристаллов обусловлена особенностями их строения, рассмотрим сначала вопросы структуры кристаллов.
При описании правильной внутренней структуры кристаллов обычно пользуются понятием кристаллической решетки. Кристаллическая решетка представляет собой пространственную сетку, в узлах которой располагаются частицы (атомы, ионы или молекулы), образующие кристалл. В основе кристаллической решетки лежит элементарная кристаллическая ячейка, представляющая собой параллелепипед минимального объема с характерным для данной решетки расположением атомов (рисунок 2.2). Если взять большое число одинаковых кристаллических ячеек и вплотную уложить их в определенном объеме, сохраняя параллельность ребер и граней, то мы будем иметь пример строения идеального монокристалла. Формы кристаллов чрезвычайно разнообразны. Изучением их занимается наука кристаллография. В 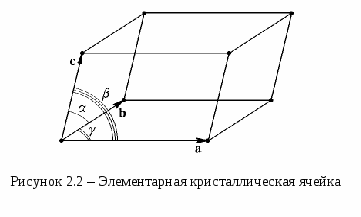 ажнейшим геометрическим свойством кристаллов, кристаллических решеток и их элементарных ячеек является симметрия (т.е. свойство совмещаться с собой) по отношению к определенным направлениям (осям) и плоскостям. В кристаллах число элементов симметрии ограничено. В них, как в конечных фигурах, различаются следующие элементы симметрии: зеркальная плоскость симметрии, поворотная ось симметрии (простая и винтовая), центр симметрии или центр инверсии. Зеркальная плоскость симметрии соответствует простому отражению в плоскости, как в зеркале. Такая плоскость делит тело на две равные части, совпадающие друг с другом всеми своими точками при отражении в этой плоскости. Простая поворотная ось симметрии - прямая линия, при повороте вокруг которой на долю окружности, равную 1/n (где n - порядок оси) фигура совмещается сама с собой всеми своими точками. Зеркально-поворотные оси сочетают одновременно действие поворота около оси на долю окружности 1/n и отражение в перпендикулярной ей плоскости. Центр симметрии, или центр инверсии, - особая точка внутри фигуры, при отражении в которой фигура совмещается сама с собой. В кристаллах встречаются оси симметрии только пяти порядков: первого, второго, третьего, четвертого и шестого. Оси пятого порядка, седьмого и выше в кристаллах запрещены, так как их существование несовместимо с представлениями о кристаллической решетке. Все вышеуказанные операции симметрии называются точечными операциями симметрии, так как они оставляют неизменной, по крайней мере одну точку фигуры. Полную совокупность элементов симметрии, характеризующую симметрию объекта, называют классом симметрии. Всего существуют 32 точечных класса (группы) симметрии. Это показал в 1867 г. русский инженер и кристаллограф А. В. Гадолин. В пространственной решетке к рассмотренным элементам симметрии - плоскость симметрии, ось симметрии, центр симметрии - добавляется новый элемент симметрии - трансляция Т=n1a+ n2b+n3c, где n1, n2, n3 - произвольные целые числа, a, b, c - векторы основных (примитивных) трансляций (см. рисунок 2.3). В 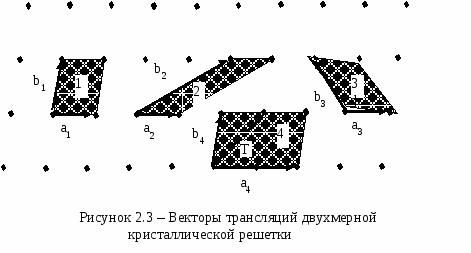 се изображенные на рисунке пары векторов a и b являются векторами трансляций решетки. Однако векторы a4 и b4 не являются примитивными векторами трансляций, поскольку вектор трансляции кристаллической решетки T нельзя выразить как Т=n1a4+ n2b4 где n1 и n2 - целые числа. Все остальные пары векторов a и b можно выбрать в качестве векторов примитивных трансляций. Параллелограммы 1, 2, 3 имеют равную площадь и любой из них можно выбрать в качестве плоской примитивной ячейки. Трансляция действует не на какую-нибудь точку решетки, а на всю решетку в целом. При перемещении решетки на трансляцию в направлении вектора трансляции решетка совмещается сама с собой всеми своими точками. В 1881 г. выдающийся русский кристаллограф Е. С. Федоров исследовал все мыслимые пространственные расположения частиц кристалла, исходя из того, что плотное заполнение пространства кристаллическими ячейками возможно только при определенной форме ячеек, и установил, что внутри 32 классов симметрии может существовать 230 различных пространственных групп (т. е. 230 типов геометрического расположения атомов в кристаллах). Несколько позже E. С. Федорова к таким же результатам пришел немецкий математик А. Шенфлис. Французский кристаллограф О. Браве в 1848 г. положил начало геометрической теории структуры кристаллов и показал, что в зависимости от соотношения величины и взаимной ориентации ребер элементарной кристаллической ячейки может существовать 14 типов кристаллических решеток (они получили название решеток Браве). Различают примитивные (простые), базоцентрированные, объемноцентрированные и гранецентрированные решетки Браве. Если узлы кристаллической решетки расположены только в вершинах параллелепипеда, представляющего собой элементарную ячейку, то такая решетка называется примитивной или простой, если, кроме того, имеются узлы в центре оснований параллелепипеда, то решетка называется базоцентрированной, если есть узел в месте пересечения пространственных диагоналей - решетка называется объемноцентрированной, а если имеются узлы в центре всех боковых граней - гранецентрированной. По форме ячейки в зависимости от углов между ее гранями , , и в зависимости от соотношения между величиной ребер а, b, с различают семь кристаллических систем (сингоний) (см. таблицу 2.1 ). Приведем примеры элементарных ячеек четырнадцати простейших кристаллических решеток, принадлежащих разным кристаллическим системам (см. рисунок 2.4 ). На рисунке 2.4 и в таблице 2.1 используются следующие обозначения: P - символ примитивной ячейки, I - объемноцентрированной, F - гранецентрированной, C - с центрированными основаниями, R - ромбоэдрической. Таблица 2.1 - Решетки Браве
Решетка Браве представляет собой совокупность одинаковых и одинаково расположенных (эквивалентных) атомов или ионов, которые могут быть совмещены друг с другом путем параллельного переноса. Не следует думать, что одна решетка Браве исчерпывает собой все атомы (ионы) данного кристалла. Сложная структура кристаллов может быть представлена как совокупность нескольких решеток Браве, вдвинутых одна в другую. Это одинаково относится как к кристаллам химических элементов, так и к кристаллам сложного химического состава. 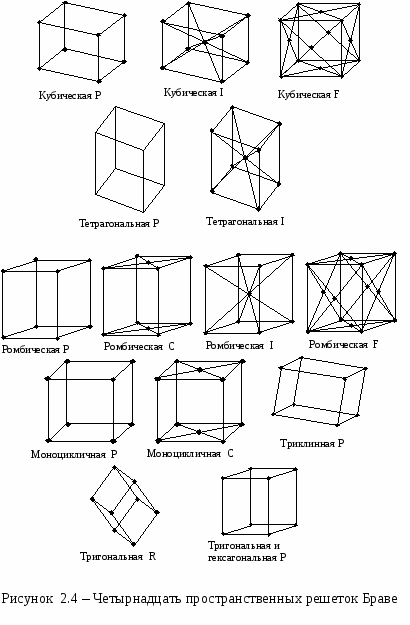 Кристаллы правильной многогранной формы встречаются очень редко, так как для роста их требуются особенно благоприятные условия: отсутствие внешних помех, равномерное охлаждение со всех сторон (при росте из расплава) или же равномерный всесторонний приток вещества, отлагающегося на поверхности кристалла (при росте из раствора). Вследствие этого судить о принадлежности кристалла к той или иной кристаллической системе только по его внешней огранке, как правило, бывает довольно трудно. Однако измерение углов между соответствующими гранями кристалла, не имеющего правильной многогранной формы, может дать ответ на вопрос о принадлежности его к определенной кристаллической системе. Периоды кристаллических решеток (расстояние между ближайшими соседями) для элементов и простейших соединений составляют всего несколько ангстрем, а для сложных неорганических и органических соединений они достигают 10-20 ангстрем. Поэтому наблюдать кристаллическую решетку непосредственно, с помощью оптического или даже электронного микроскопа не представляется возможным. Исключение из этого составляют кристаллы весьма сложных органических соединений - глобулярных белков и вирусов, период решетки которых достигает нескольких сотен ангстрем. Такие кристаллы можно наблюдать с помощью электронного микроскопа. Не увенчались успехом также попытки доказать решетчатую структуру кристаллов с помощью дифракции света, так как длина световой волны в103-104 раз больше периода решетки. Лишь открытие явления дифракции рентгеновских лучей в кристаллах (1912 г.) явилось прямым доказательством существования кристаллической решетки. С помощью метода рентгенографииможно установить геометрические параметры кристаллической решетки данного кристалла, т. е. найти ребра и углы элементарной ячейки. Таким образом, расшифровка кристаллической структуры вещества имеет сейчас прочную экспериментальную базу - рентгеноструктурный анализ - и не встречает принципиальных затруднений. 2.3 Образование плоскостей и направлений в кристалле 2.3.1 Индексы Миллера Для обозначения кристаллографических плоскостей в настоящее время общепринятой является система индексов Миллера. Поясним ее сущность. В 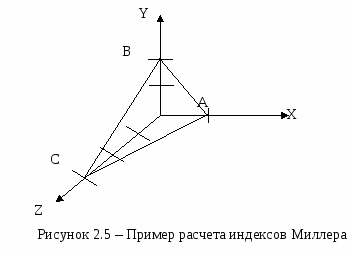 ыберем систему координат, оси которых совпадают с тремя ребрами элементарной кристаллической ячейки. Начало координат поместим в одном из узлов решетки, в котором пересекаются эти ребра. Осевые единицы выберем равными длине ребер кристаллической ячейки, т. е. масштаб по оси X будет равен а, по оси Y - b и по оси Z - с. Разномасштабность осей координат вполне оправдывает себя, так как позволяет ввести наиболее рациональную систему индексов. Положение любой плоскости в пространстве определяется тремя точками. В выбранной системе координат удобно в качестве трех опорных точек взять точки пересечения заданной плоскости с осями координат. Пусть определяемая узловая плоскость S пересекает оси координат в точках А, В, С (см. рисунок 2.5) и отсекает по осям отрезки х=1, y=2, z=3. Далее поступают по следующей схеме.
Миллеровские индексы плоскостей заключаются в круглые скобки - (632), знак отношения между индексами не ставится. Если плоскость параллельна какой-либо оси, ее проекция на эту ось равна бесконечности. Для такой плоскости соответствующий индекс Миллера равен нулю. Если плоскость отсекает некоторый отрезок с отрицательным знаком, то соответствующий индекс Миллера будет также отрицательным, и черточка ставится сверху над индексами Рассмотрим пример кубической решетки. Нас интересует плоскость abcd (см. рисунок 2.6). Пусть ребро куба равно 1. Плоскость abcd имеет индексы Миллера (100). Если мы хотим обозначить не одну плоскость, а семейство плоскостей, то индексы Миллера берутся в фигурные скобки {100}. Плоскость cdeq имеет индексы Миллера (101). Плоскость deg имеет индексы Миллера (111). Таким образом, мы описали три основные плоскости для кубической решетки (см. также рисунок 2.7). Индексы Миллера для направления представляют собой набор целых чисел, отношение которых друг к другу равно наименьшим проекциям вектора, параллельного выделенному направлению, но проходящего через начало координат. Индексы Миллера для направлений в отличие от индексов Миллера для плоскостей помещаются не в круглые скобки, а в квадратные скобки. Рассмотрим тот же пример кубической решетки (см. рисунок 2.6): Направление ОХ: [100]. Н 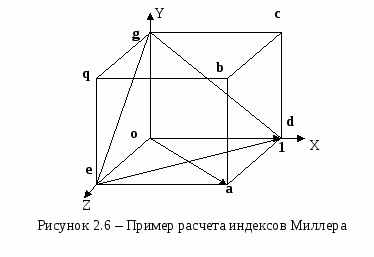 аправление ОА: [101]. Направление перпендикулярное плоскости (111): [111]. |
