|
|
Физика твердого тела (тексты лекций). Гомельский государственный университет имени Франциска Скорины С. А. Хахомов, А. В. Семченко, Ю. В. Никитюк физика твердого тела
Колебания цепочки атомов 2-х сортов
Предположим, что имеем цепочку легких атомов с массой m и тяжелых с массой M (см. рисунок 7.5). Расстояние между атомами - a.
П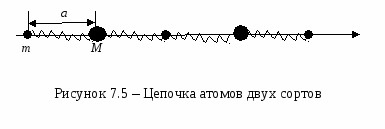
усть легкие атомы занимают четные положения, а тяжелые - нечетные. Запишем законы движения для легких и тяжелых частиц. Обозначим u2n - смещение атома с массой m, u2n-1 - смещение атома с массой M. Учтем влияние лишь ближайших соседей на движение данного атома. Влиянием более удаленных частиц будем пренебрегать.
Тогда для легких частиц:
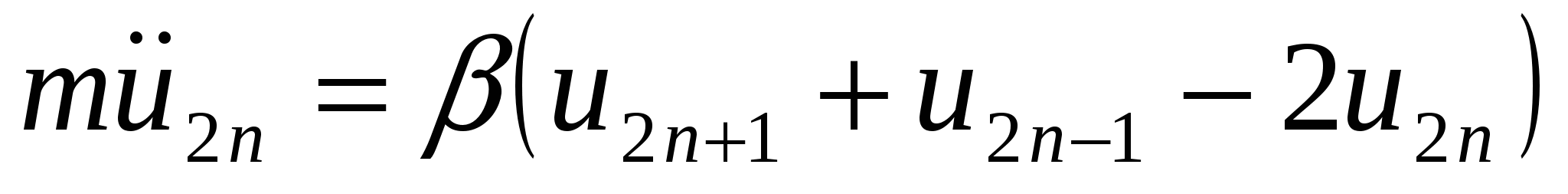 , ,
а для тяжелых частиц:
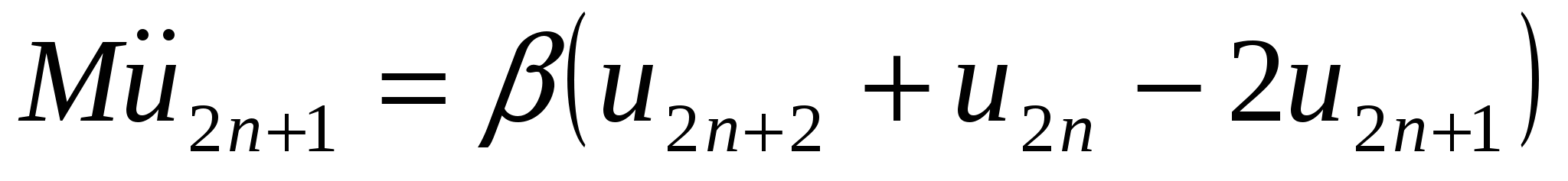 . .
С учетом того, что колебания атомов разных масс могут происходить с различными амплитудами u1 и u2, решение этой системы уравнений будем искать в следующем виде:
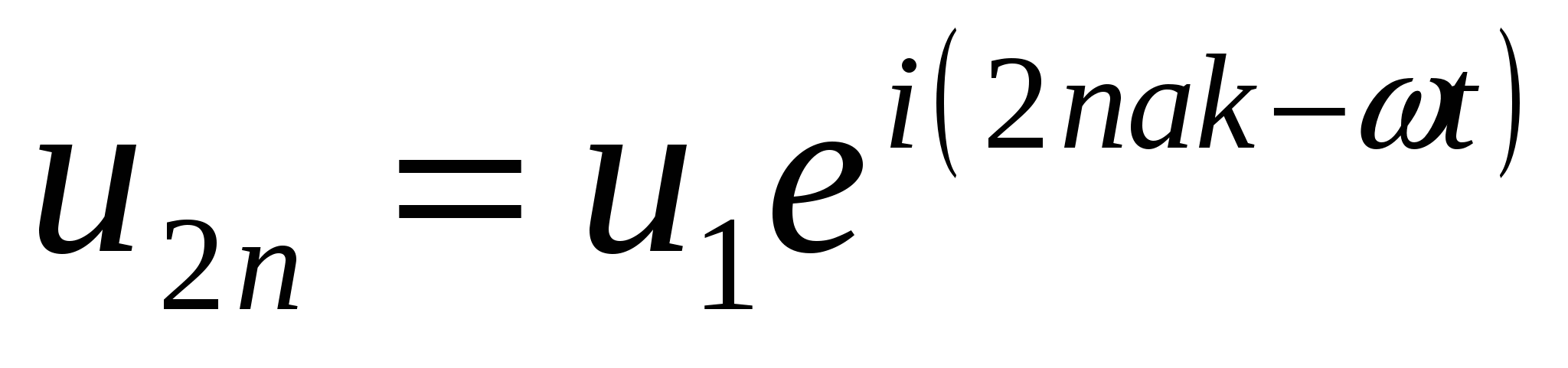 , ,
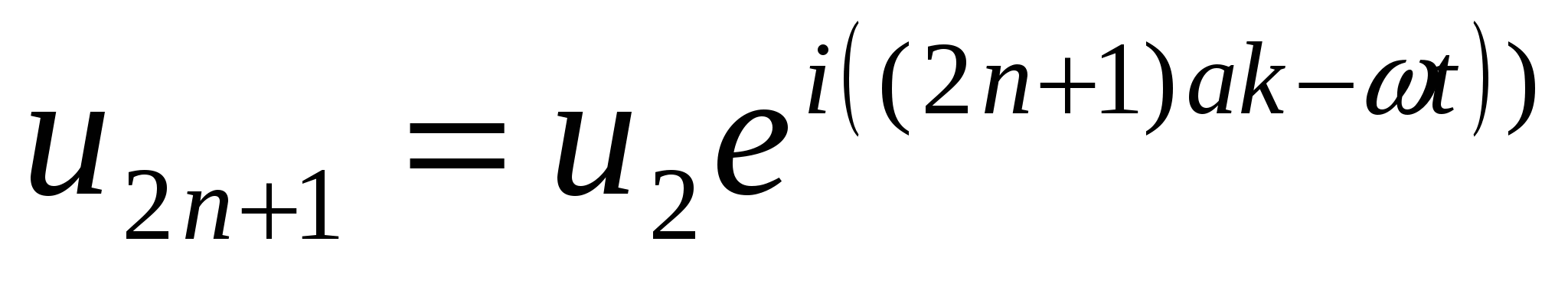 . .
Подставим эти решения в уравнения движения и, сократив общий множитель 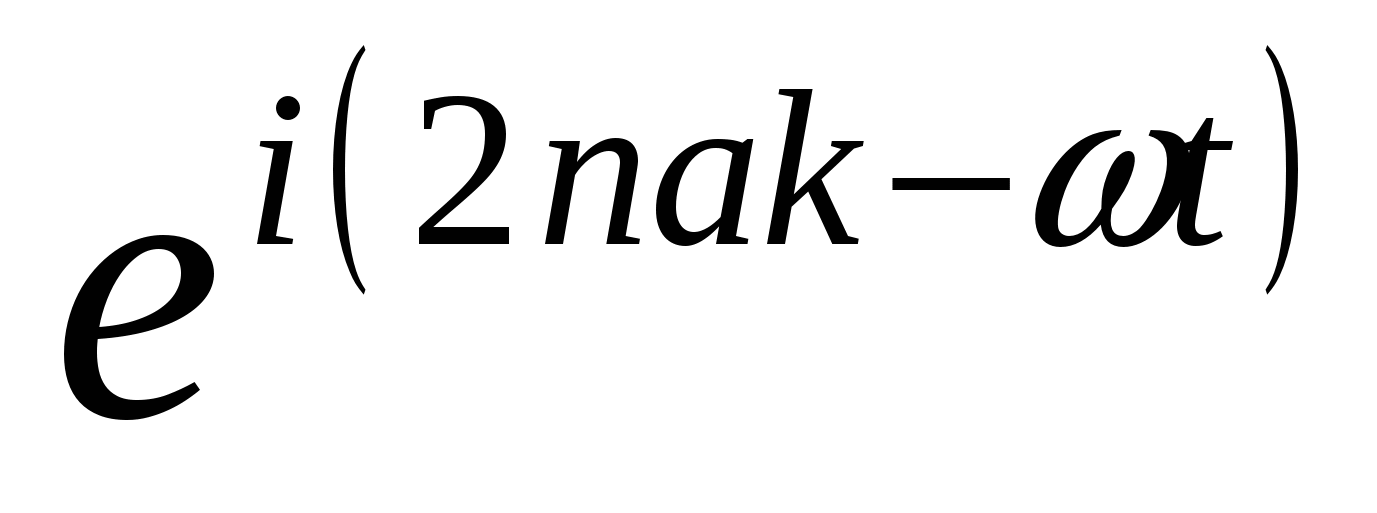 в каждом из уравнений, получим систему уравнений относительно u1 и u2: в каждом из уравнений, получим систему уравнений относительно u1 и u2:
(2-m2) u1 -2 cos (ka) u2=0
-2 cos (ka) u1 + (2-M2) u2=0
Система линейных однородных уравнений будет иметь ненулевое решение в том случае, если определитель равен нулю.
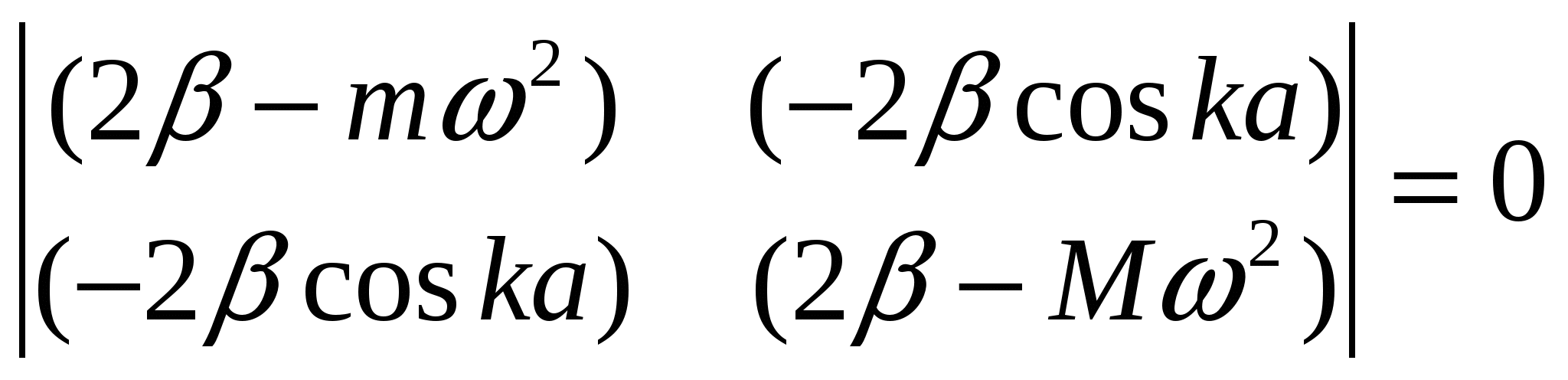
Отсюда получаем уравнение, связывающее частоту и волновое число k:
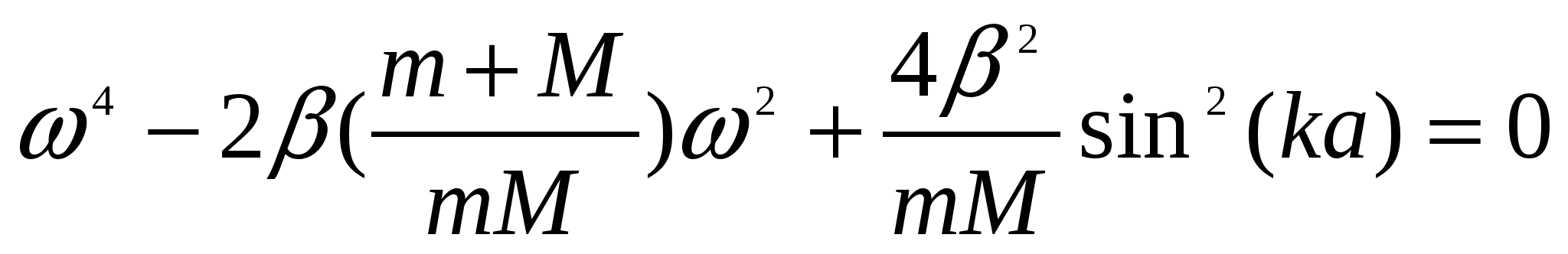
Корни этого уравнения
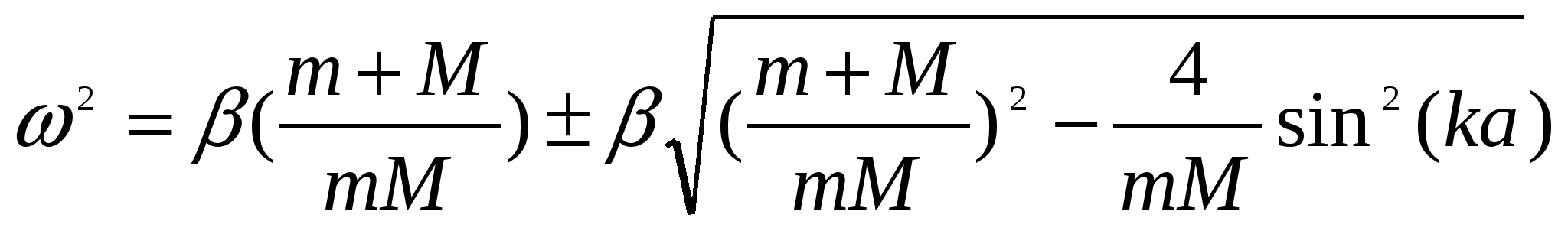 . .
Отрицательные значения не имеют физического смысла. Поэтому каждому волновому числу k соответствуют два значения , а, следовательно, и две моды колебаний.
Итак, решение задачи о колебаниях атомов двух сортов в цепочке, приводит к двум кривым зависимости (k), которые получили название двух ветвей закона дисперсии (см. рисунок 7.6). Нижнюю кривую называют акустической ветвью, верхнюю - оптической ветвью. Во всем интервале изменений волновых чисел k частота оптических колебаний больше частоты акустических.
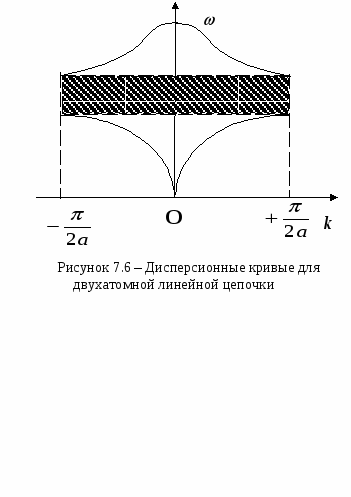
Нижняя ветвь ведет себя аналогично кривой для одноатомной цепочки, поэтому она получила название акустической. Верхняя ветвь достигает максимальных значений при k=0 и принимает минимальные значения при 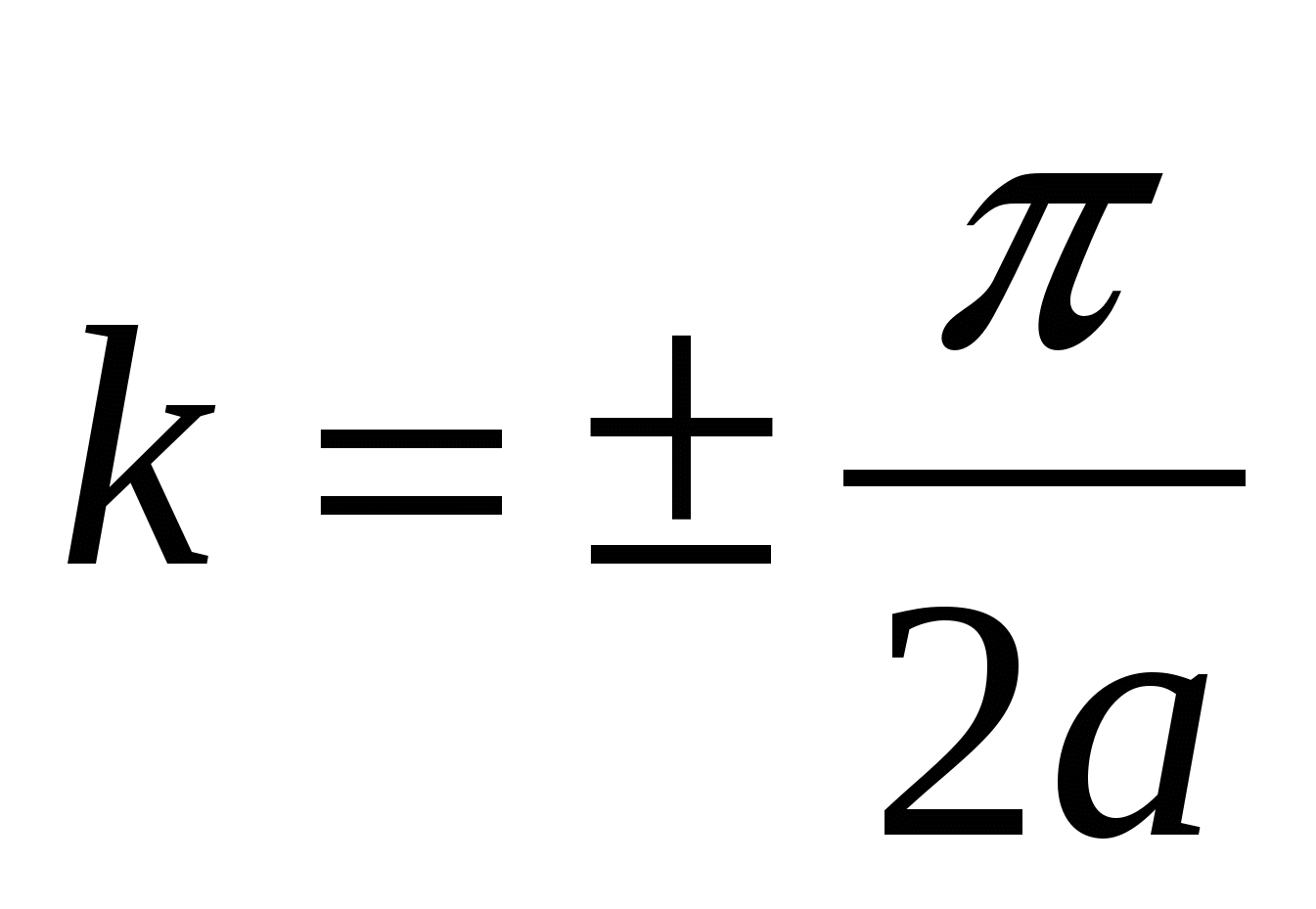 . Эту ветвь называют оптической, так как длинноволновые оптические моды в ионных кристаллах могут взаимодействовать с электромагнитным излучением. . Эту ветвь называют оптической, так как длинноволновые оптические моды в ионных кристаллах могут взаимодействовать с электромагнитным излучением.
Как видно из рисунка 7.6, две ветви разделены полосой запрещенных частот (заштрихованная область на рисунке), в которой уравнения движения не имеют решения. Однако если в цепочке заменить, например, один или несколько атомов массы M на атомы массы m, т.е. ввести в структуру дефекты, то в запрещенной области частот появятся решения, которые называют локальными модами.
Выясним физический смысл различия между акустическими и оптическими модами колебаний атомов в цепочке.
Если рассмотреть нижнюю ветвь колебаний, то для нее амплитуды колебаний легких и тяжелых частиц будут равны (см. рисунок 7.7). Отсюда следует, что для нижней ветви спектра, колебания, смещается синхронно с одинаковыми амплитудами. Фактически для нижней ветви спектр колебаний будет представлять синусоиду, в которой смещаются вверх - вниз синхронно легкие и тяжелые атомы и соответственно их центры масс.
Р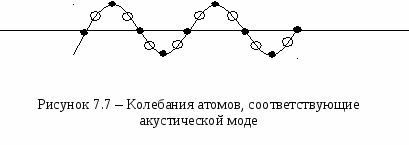
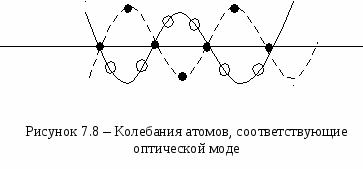
ассмотрим верхнюю ветвь колебаний. Для колебания легких и тяжелых частиц происходят в противофазе, причем центр масс не меняет своего положения (см. рисунок 7.8).
Таким образом, в цепочке, состоящей их атомов двух сортов атомов, происходит разделение колебаний на акустическую и оптическую ветви. При этом частота оптических колебаний слабо зависит от волнового числа к, а для акустической ветви эта зависимость более сильная. Естественно предположить, что с усложнением модели и ее обобщением на 3-х мерный случай, спектр колебания также будет представлять набор ветвей колебаний (часть акустических, часть оптических). Спектр колебания реальных материалов также может быть представлен в виде ветвей колебаний, что соответствует экспериментальным данным.
7.4 Фононы
Колебания передаются от частицы к частице и распространяются в виде волн. Всякое колебание можно разложить на два поперечных и одно продольное. Любое сложное (не синусоидальное) колебание можно представить в виде суммы синусоидальных колебаний разных периодов и амплитуд (метод Фурье). Таким образом, в кристалле установится система продольных и поперечных синусоидальных волн. Полное число независимых волн в кристалле равно утроенному числу узлов кристаллической решетки. Эти продольные и поперечные волны доходят до поверхности кристалла, отражаются от нее и, налагаясь на встречные волны, образуют сложную систему стоячих волн.
Аналогично тому, как в струне, закрепленной на концах, могут возникать стоячие волны вполне определенных длин (в длине струны должно укладываться целое число полуволн), в кристалле тоже устанавливаются серии дискретных стоячих волн, связанные с размерами кристалла и с его упругими свойствами.
Механизм этих тепловых упругих волн в кристаллах аналогичен механизму звуковых волн, поэтому их обычно называют акустическими волнами. Диапазон частот тепловых волн очень широк - от звуковых частот 102 до 1013 Гц.
Скорость распространения тепловых волн совпадает со скоростью распространения звука. Энергия распределяется между всеми видами волн, но большая часть ее приходится на короткие волны. Теория тепловых упругих волн в кристаллах была разработана голландским физиком Дебаем в 1912 г.
Подобно энергии электромагнитных волн, энергия тепловых акустических волн тоже квантована. Аналогично кванту световой энергии фотону, квант звуковой энергии назван фононом.Энергия фонона выражается произведением постоянной Планка на частоту:
E=hν
где Е - энергия фонона, h- постоянная Планка, ν - частота колебания.
Фононы относятся к категории квазичастиц. Основное отличие квазичастиц от обычных частиц (электронов, протонов, нейтронов, фотонов) заключается в том, что квазичастицы не могут существовать в вакууме: для своего возникновения и существования они нуждаются в некоторой вещественной среде.
Фононы являются элементарными носителями движения в системе частиц, входящих в кристаллическую решетку и связанных друг с другом силами взаимодействия.
В газах частицы одновременно выполняют две функции: они являются элементарными «кирпичиками» самого вещества газа, т. е. выполняют функцию структурных единиц системы, и одновременно являются элементарными носителями движения в этой системе. В твердом теле две эти функции разделяются: атомы, молекулы или ионы представляют собой структурные единицы твердого тела, а фононы - структурные единицы переноса энергии в твердом теле.
В соответствие с постулатами квантовой механики частицы не могут находиться в покое даже при абсолютном нуле, так как это противоречит принципу неопределенности. Если частица покоится, то ее координаты точно фиксированы, но тогда неопределенность в импульсе частицы будет бесконечно большой, т. е. частица будет обладать большой кинетической энергией. Это противоречие позволяет сделать заключение, что самое низкое энергетическое состояние тела при Т = 0° К тоже будет особым состоянием движения - так называемое нулевое движение. Особенность нулевого движения состоит в том, что оно не имеет дискретных характеристик, квазичастицы при этом как бы отсутствуют. Свойства твердого тела определяются не только свойствами его частиц и квазичастиц, но и характером нулевого движения.
Совокупность динамических свойств квазичастиц в кристалле и характер его основного состояния (нулевого движения) образует то, что принято называть энергетическим спектромтвердого тела. Энергетический спектр фононов можно установить, изучая неупругое рассеяние медленных (тепловых) нейтронов на фононах решетки.
Дискретность (квантовый характер) дебаевских тепловых волн проявляется при температурах ниже характеристической температуры Дебая , определяемой соотношением
=hνмакс/k,
где νмакс - максимальная частота тепловых колебаний частиц, свойственных данному твердому телу, k- постоянная Больцмана.
Сущность характеристической температуры можно пояснить следующими рассуждениями. Из классической теории газовых теплоемкостей известно, что средняя кинетическая энергия теплового движения молекулы, приходящаяся на одну степень свободы равна 1/2kT. В колебательном тепловом движении узлов кристаллической решетки средние значения кинетической и потенциальной энергии одинаковы, следовательно, полная энергия, приходящаяся на одну степень свободы, будет вдвое больше, т. е. равна kT. Когда средняя энергия, приходящаяся на одну степень свободы, будет значительно превосходить максимальную энергию фононов, тогда могут возбуждаться колебания любых возможных для данного твердого тела частот, и квантовый характер тепловых волн не проявляется. Если же энергия kTпри низких температурах становится меньше энергии фононов максимальной частоты, то тогда высокочастотные колебания уже не могут быть возбуждены. Таким образом, температурным рубежом, ниже которого начинает проявляться квантовый характер тепловых волн, является характеристическая температура Дебая.
Дебаевская температура зависит от величины сил связи между узлами кристаллической решетки и является параметром твердого тела, который фигурирует в описании ряда свойств твердого тела (электропроводность, теплопроводность и др.). Для большинства веществ дебаевская температура лежит в пределах 300 - 800 ºС, но есть такие вещества, для которых она значительно выше. Например, у алмаза характеристическая температура около 2000º С.
Лекция 8
Тепловые свойства твердых тел
8.1 Теплоемкость
8.1.1 Закон Дюлонга и Пти
8.1.2 Теория теплоемкости Дебая
8.1.3 Электронная теплоемкость
8.2 Теплопроводность
8.2.1 Понятие о коэффициенте теплопроводности
8.2.2 Механизмы теплопроводности твердых тел
8.1 Теплоемкость
8.1.1 Закон Дюлонга и Пти
Из молекулярной физики известно, что теплоемкость при постоянном объеме есть первая производная по температуре от внутренней энергии тела:
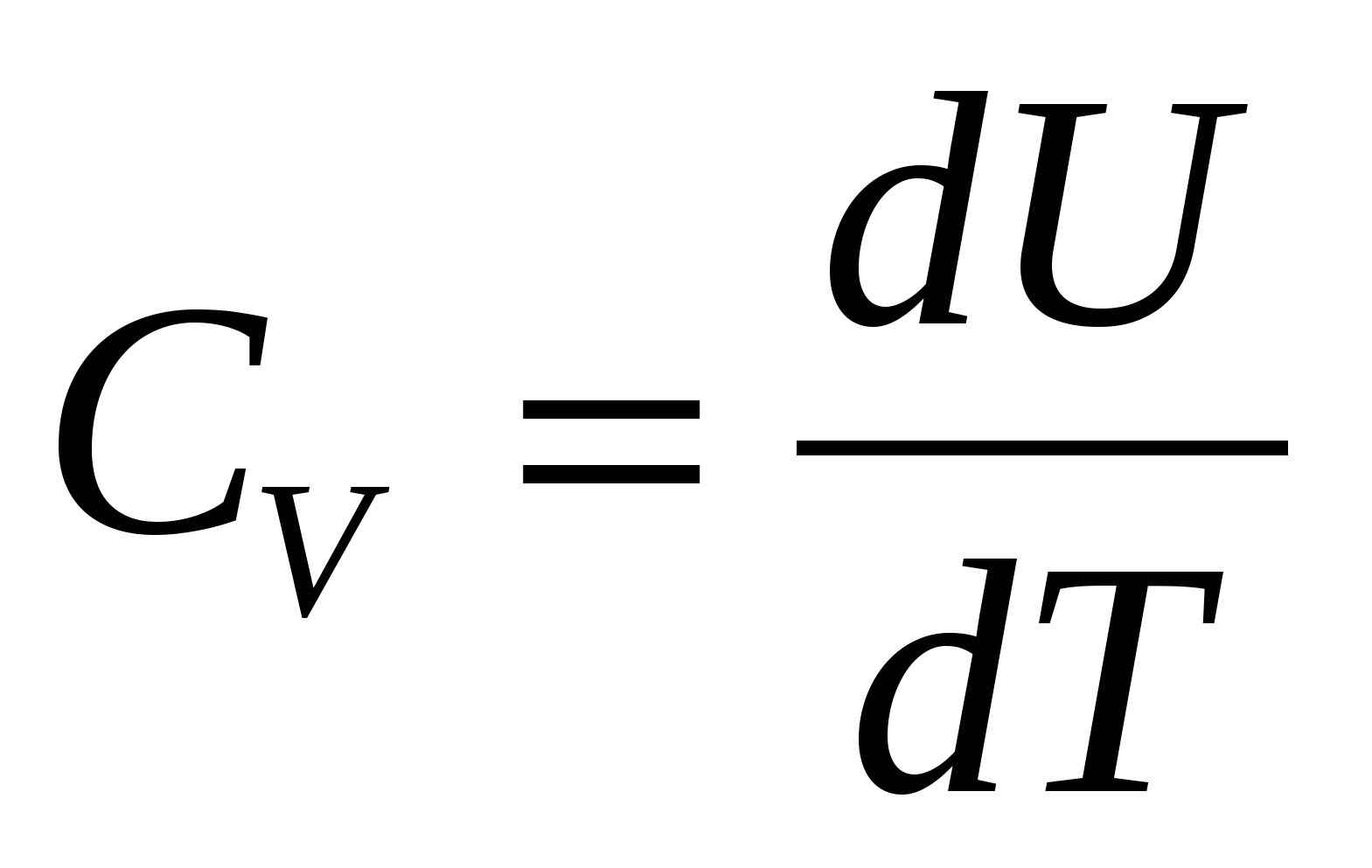
или для твердых тел
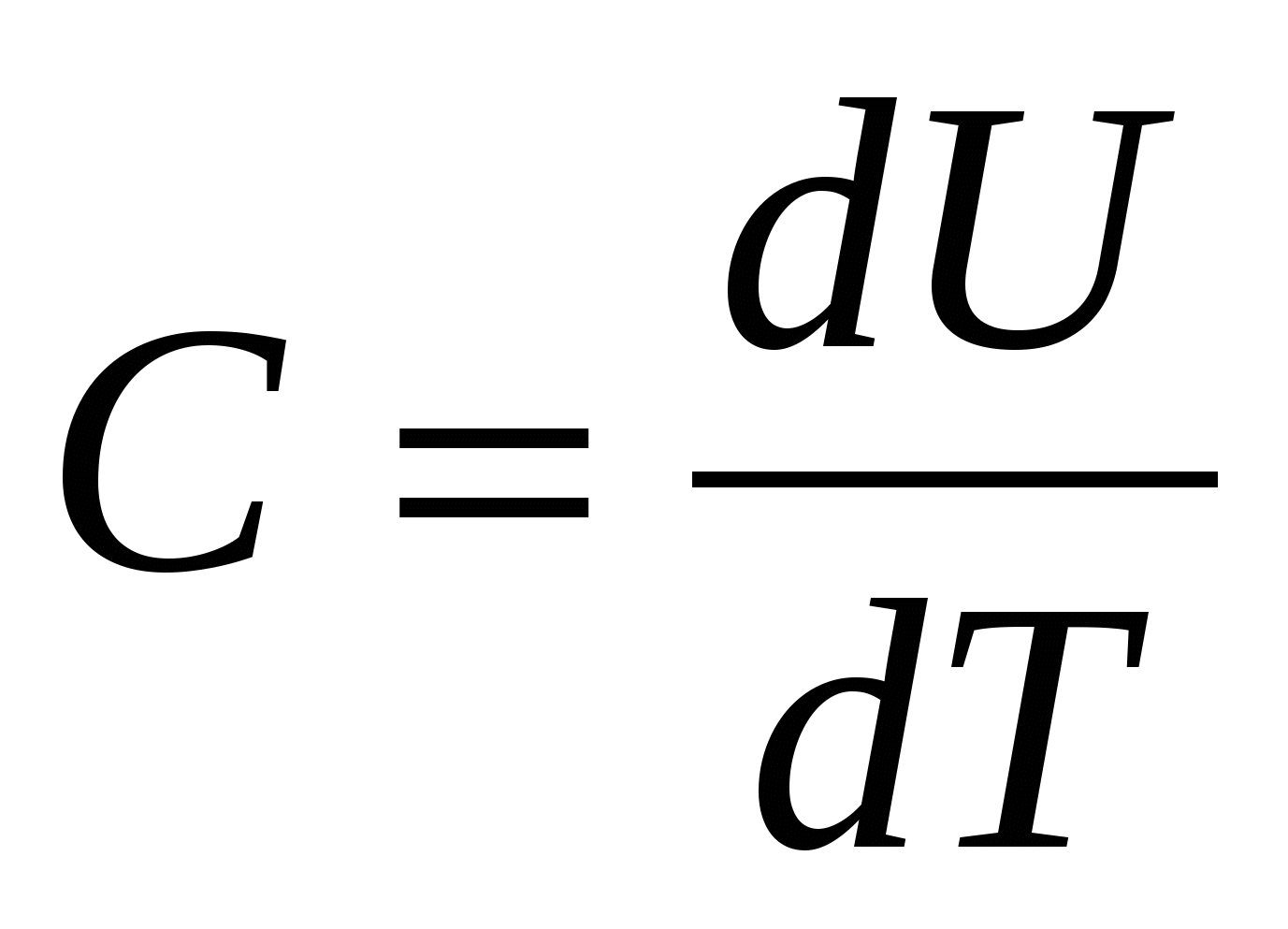 . .
Допустим, что для твердого тела справедлива гипотеза о равномерном распределении энергии теплового движения по степеням свободы. Указанное допущение является применением классической теории теплоемкостей к твердому телу, и в соответствии с ним на каждую степень свободы приходится энергия ε =1/2 kT.
В качестве модели выберем твердое тело, атомы которого совершают малые колебания около положения равновесия в узлах кристаллической решетки. Каждый атом независимо от соседей колеблется в трех взаимно перпендикулярных направлениях. То есть он имеет три независимые степени свободы. Такой атом можно уподобить совокупности трех линейных гармонических осцилляторов. При колебании осциллятора последовательно происходит преобразование кинетической энергии в потенциальную и наоборот. Поскольку средняя кинетическая энергия, составляющая ½ kTна одну степень свободы, остается неизменной, а средняя потенциальная энергия равна средней кинетической, то полная энергия осциллятора, равная сумме кинетической и потенциальной энергий, будет составлять kT.
Тогда полная энергия колебания одного узла решетки выразится формулой
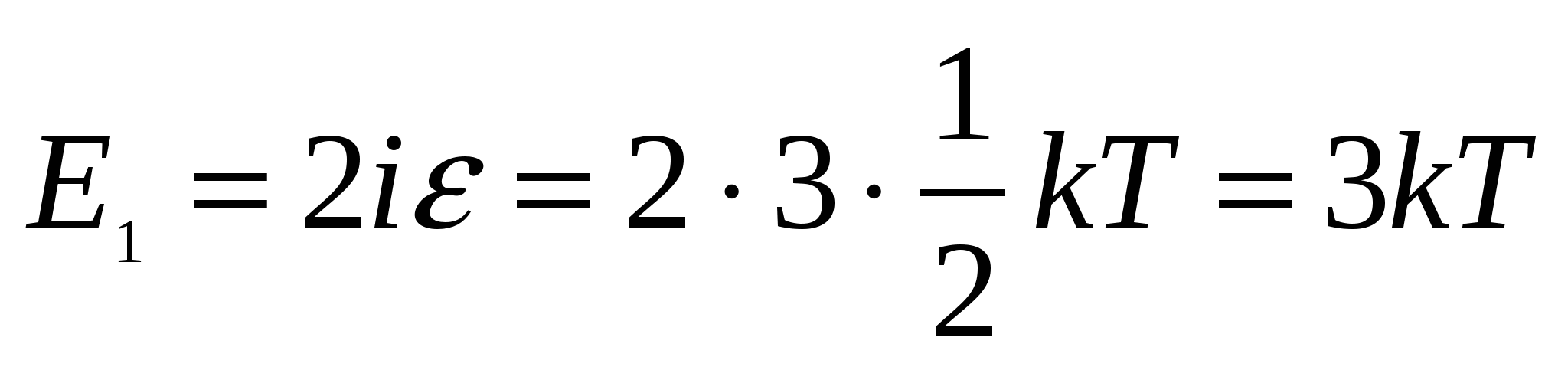 , ,
так как для поступательного движения точки число степеней свободы i= 3.
Тогда полная средняя тепловая энергия такой системы равна:
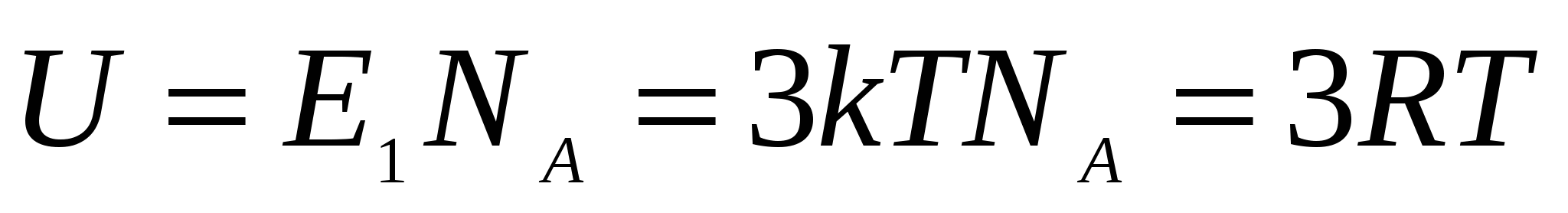 , ,
где k - постоянная Больцмана, NA- число Авогадро, R- универсальная газовая постоянная.
Тогда теплоемкость, как приращение энергии, соответствующее повышению температуры на один градус, будет равна:
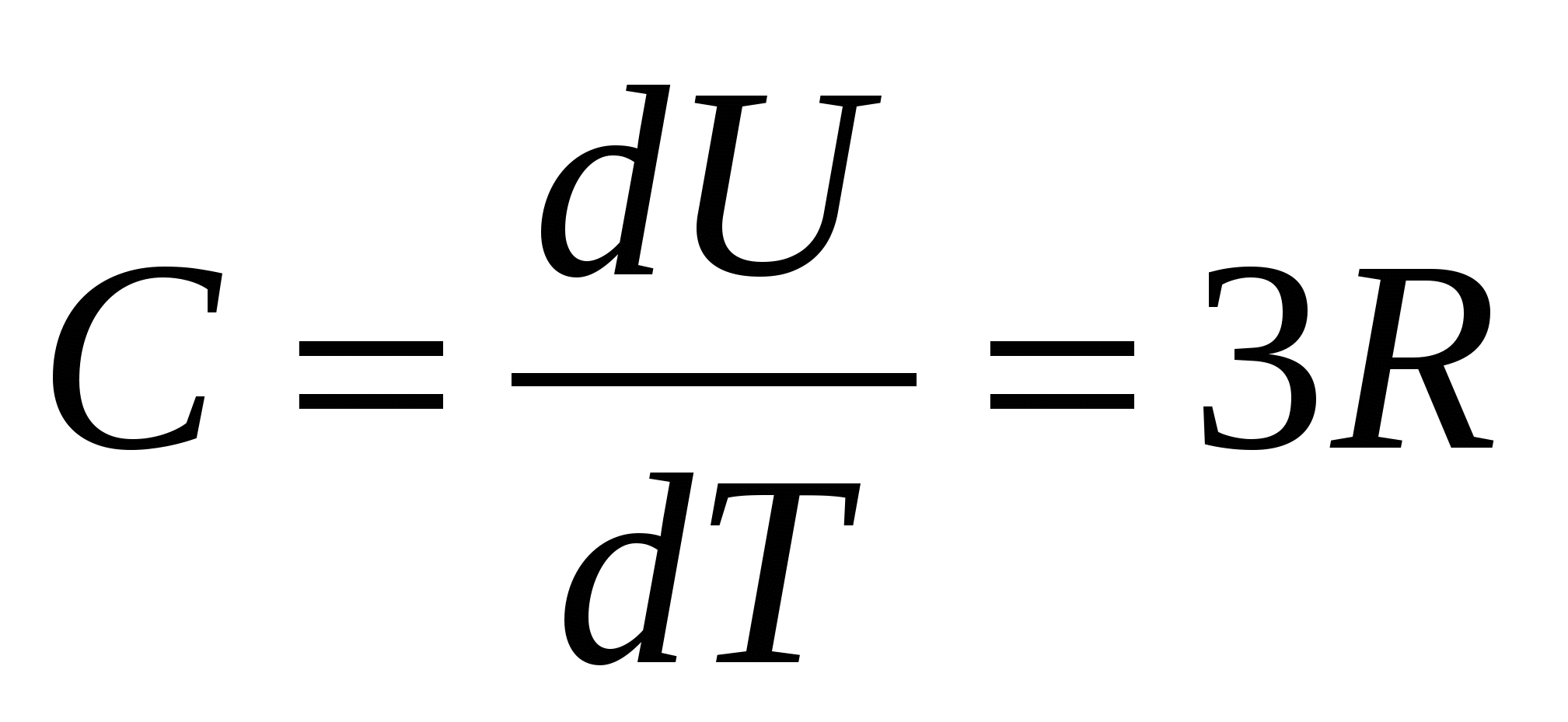 . .
Таким образом, атомные теплоемкости всех химически простых кристаллических тел при достаточно высокой температуре одинаковы и равны 25 Дж∙K-1∙моль-1.
Эта закономерность давно известна в физике как закон Дюлонга и Пти. Французские физики Дюлонг и Пти, исследуя теплоемкости твердых тел, еще в 1819 г. (задолго до создания классической теории теплоемкостей) из опытных данных установили этот закон.
Таблица 8.1 - Значения теплоемкости некоторых материалов при комнатной температуре
Элемент
|
С,
Дж∙K-1∙моль-1
|
Элемент
|
С,
Дж∙K-1∙моль-1
|
Алюминий
|
25,7
|
Серебро
|
25,7
|
Железо
|
26,8
|
Цинк
|
25,5
|
Золото
|
26,6
|
Йод
|
27,6
|
Медь
|
24,7
|
Кремний
|
19,4
|
Олово
|
27,8
|
Бор
|
10,5
|
Платина
|
26,3
|
Алмаз
|
5,7
|
Из таблицы 8.1 видно, что для многих твердых тел (главным образом металлов) комнатная температура уже является достаточно высокой, чтобы колебания атомов можно было рассматривать как независимые. Но для алмаза, бора и кремния получается большое отклонение от закона Дюлонга и Пти, следовательно, комнатная температура для них не является достаточно высокой. Атомная теплоемкость алмаза приближается к 25 Дж∙K-1∙моль-1 лишь при температуре около 1000° С.
Если аналогичные рассуждения произвести для ионных кристаллов, то можно сделать вывод, что двухатомные кристаллы должны иметь С = 50 Дж∙K-1∙моль-1, а трехатомные – С = 75 Дж∙K-1∙моль-1 и т. д. (в моле двухатомного кристалла содержится 2naузлов решетки, трехатомного - 3na). Эта закономерность оправдывается для ряда кристаллов (см. таблицу 8.2).
Таблица 8.2 - Значения теплоемкости некоторых ионных кристаллов при комнатной температуре
Кристалл
|
С, Дж∙K-1∙моль-1
|
CuO
|
47,3
|
NaCl
|
50,7
|
СаС12
|
76,2
|
ВаС12
|
77,9
|
На первый взгляд кажется, что выводы классической теории теплоемкостей применительно к твердому телу дают хорошее совпадение с экспериментальными данными. Но более глубокое рассмотрение вопроса приводит к заключению о том, что эти выводы находятся в резком противоречии с опытом.
Серьезным недостатком этой теории является вывод о независимости теплоемкости твердого тела от температуры.
Так в соответствие с классической теорией: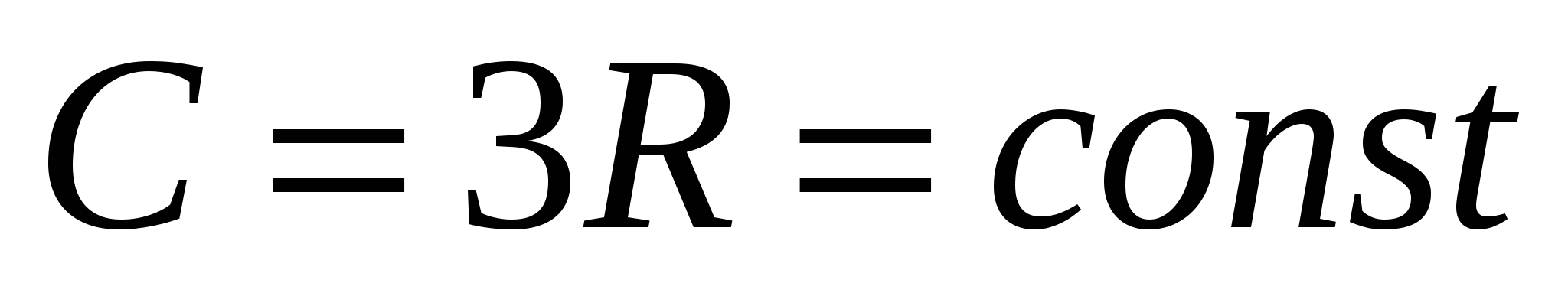 . .
На самом же деле теплоемкость уменьшается с понижением температуры и стремится к нулю при приближении температуры к абсолютному нулю.
О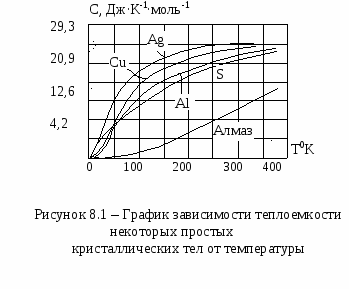
бщий характер зависимости теплоемкости некоторых простых кристаллических тел от температуры графически изображен на рисунке 8.1.
Из рисунка 8.1 видно, что только при определенных достаточно высоких температурах теплоемкость твердых тел достигает величины 25 Дж∙K-1∙моль-1, соответствующей закону Дюлонга и Пти. Какова же эта температура?
8.1.2 Теория теплоемкости Дебая
С позиции классической теории теплоемкости нельзя объяснить не только этот вопрос, но и сам факт изменения теплоемкости с температурой. Для объяснения этого факта необходимо принять модель твердого тела, предложенную Дебаем.
Исходя из этой модели можно сделать вывод, что теплоемкость твердого тела должна существенно уменьшаться при понижении температуры кристалла ниже его характеристической (дебаевской) температуры. То есть когда энергия, приходящаяся на одну степень свободы, становится недостаточной для возбуждения высокочастотных фононов. Следовательно, температура, при которой выполняется закон Дюлонга и Пти, должна быть выше характеристической температуры данного вещества. Значения характеристических температур для некоторых веществ приводятся в таблице 8.3.
Таблица 8.3 - Значения характеристических температур для некоторых веществ
Вещество
|
, °К
|
Бериллий
|
1160
|
Магний
|
406
|
Железо
|
467
|
Медь
|
339
|
Алюминий
|
418
|
Алмаз
|
2000
|
Кремний
|
658
|
Германий
|
366
|
Свинец
|
94
|
О том, что дебаевская температура не является абстракцией, введенной для пояснения квантовых представлений в модели твердого тела Дебая, а характеризует реально существующий параметр твердого тела, можно судить по рисунку 8.2.
И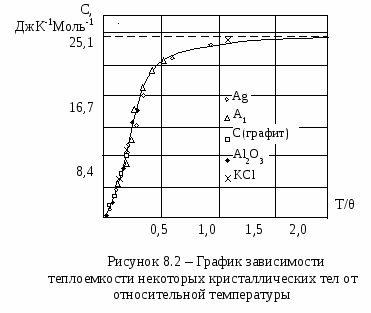
сследуя вопрос о внутренней энергии кристаллов, Дебай нашел, что при температурах, близких к абсолютному нулю, внутренняя энергия твердого тела пропорциональна четвертой степени абсолютной температуры
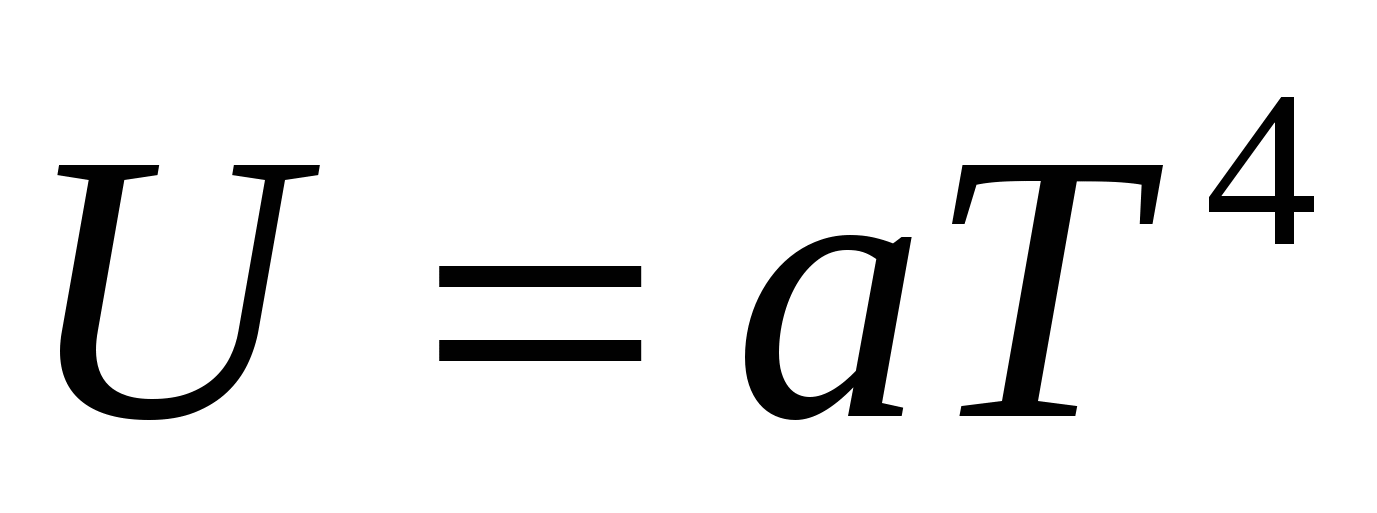 , ,
где а - постоянный множитель, зависящий от природы кристалла.
Из этого соотношения можно найти выражение для теплоемкости
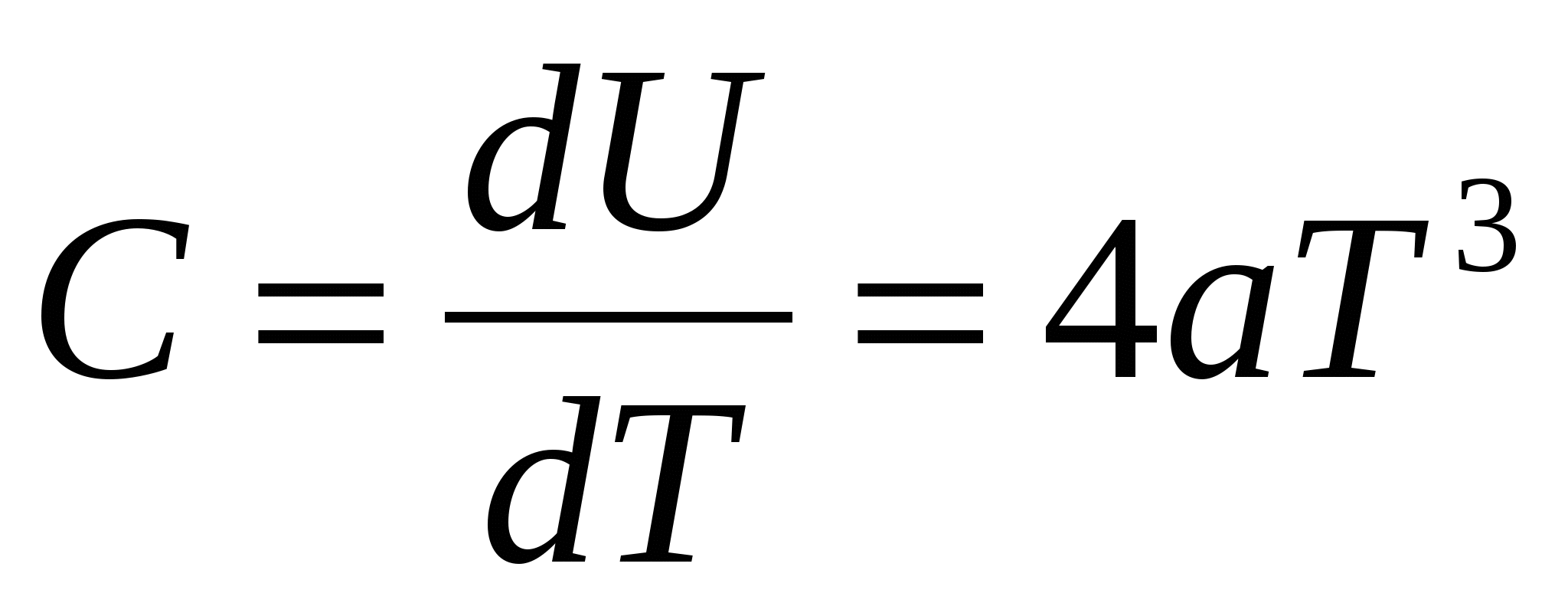 . .
Следовательно, вблизи абсолютного нуля теплоемкость твердого тела пропорциональна кубу абсолютной температуры. Эта закономерность носит название закона кубов Дебая.
Область применения закона кубов лежит ниже температуры, равной /50. При более высоких температурах от /50 до находится промежуточная область, для которой количественная связь между теплоемкостью и температурой определяется для каждого конкретного вещества отдельно. Выше характеристической температуры , как указывалось ранее, теплоемкость твердого тела не зависит от температуры (закон Дюлонга и Пти).
Опытные исследования теплоемкостей различных кристаллических тел при низких температурах показали, что закон кубов Дебая оправдывается не для всех кристаллов, а только для таких, для которых атомы в кристаллической решетке связаны со своими соседями примерно одинаково прочно во всех трех направлениях. Для слоистых кристаллов типа графита, в которых силы связи между соседними атомами внутри слоя значительно больше сил связи между ближайшими атомами из двух соседних слоев, теплоемкость при температурах, близких к абсолютному нулю, оказывается пропорциональной квадрату абсолютной температуры. Обнаружены и такие кристаллы, для которых теплоемкость около абсолютного нуля пропорциональна первой степени температуры. Такие кристаллы имеют нитевидное строение. Силы связи внутри нити много больше, чем между соседними нитями.
Теория Дебая приводит к выводам, которые хорошо совпадают с экспериментальными данными в широком интервале температур, но и она не свободна от недостатков. Трудно, например, согласиться с тем, что энергия кристалла отождествляется с энергией стоячих волн. В стоячей волне узлы и пучности закономерно распределены в пространстве, поэтому исключается возможность тепловых флуктуаций, совершенно неизбежных при тепловом движении.
Дебаевская модель твердого тела является упрощенным представлением твердого тела в виде изотропной упругой среды, способной совершать колебания в конечном интервале частот. Поэтому и выводы этой теории (например, зависимость теплоемкости от температуры) хорошо совпадают с экспериментальными данными только для кристаллов с простыми решетками. К телам сложной структуры теория Дебая неприменима, так как энергетический спектр колебаний таких тел оказывается чрезвычайно сложным. В молекулярных кристаллах, например, кроме поступательно-колебательного движения молекулы как целого, приходится учитывать ее вращательные колебания и колебания атомов или групп атомов внутри молекулы.
|
|
|
 Скачать 1.46 Mb.
Скачать 1.46 Mb.





