Физика твердого тела (тексты лекций). Гомельский государственный университет имени Франциска Скорины С. А. Хахомов, А. В. Семченко, Ю. В. Никитюк физика твердого тела
 Скачать 1.46 Mb.
|
Кристаллы с водородными связямиВ особый класс по типу связи выделяются кристаллы с водородными связями, хотя водородная связь является одним из видов межмолекулярного взаимодействия. В отличие от атомных кристаллов, у которых силы взаимодействия обусловлены обобществлением электронов, силы связи для кристаллов с водородными связями обусловлены обобществлением протонов. Водородная связь между двумя молекулами осуществляется водородным атомом, который, будучи химически связан с одной молекулой, одновременно взаимодействует с атомом кислорода другой молекулы. Такая связь может быть как одинарной, так и двойной. Полагают, что водородная связь может осуществляться с атомами фтора, натрия, хлора и серы. Соединения с водородной связью обладают тенденцией к полимеризации. Водородная связь является важнейшей формой взаимодействия между молекулами воды, она является одной из причин, побуждающих молекулы ассоциировать в группы из двух, четырех или восьми молекул, что обуславливает аномальные физические свойства воды и льда. 4.6 Сопоставление различных типов связей Классификация кристаллов по типам связи весьма условна. Многие тела трудно отнести к тому или иному классу кристаллов по типу связи. Но, тем не менее, приближенная классификация кристаллов по типам связи полезна, потому что знание преобладающего типа связи позволяет оценить энергию связи кристалла. Под энергией связи понимается энергия, необходимая для разъединения твердого тела на отдельные атомы, молекулы или ионы (в зависимости от типа кристалла: ковалентные и металлические кристаллы нужно разделить на атомы, ионные - на ионы, молекулярные и кристаллы с водородными связями - на молекулы). В таблице 4.1 приводится классификация кристаллов по типам связей с указанием энергии связи. Вандерваальсова связь является наиболее универсальной, она возникает между любыми частицами, но это наиболее слабая связь, энергия ее примерно на два порядка ниже энергии связи ионных и ковалентных кристаллов. Почти на порядок выше энергия связи кристаллов с водородными связями. Таблица 4.1 - Классификация кристаллов по типам связей с указанием энергии связи
Энергия металлической связи, возникающая в результате обобществления валентных электронов, по порядку величины сравнима с энергией связи ионных и ковалентных кристаллов, но все же меньше последней в несколько раз. Лекция 5 Дефекты в кристаллах 5.1 Классификация дефектов в кристаллах 5.2 Точечные дефекты в кристаллах 5.3 Дислокации 5.4 Границы зерен 5.5 Прочность твердых тел Изложенные ранее рассуждения о строении кристаллов и о кристаллической решетке, строго говоря, относятся только к так называемым идеальным кристаллам. Всякий же реальный кристалл не имеет такой совершенной структуры и обладает рядом нарушений идеальной пространственной решетки, которые называются дефектами в кристаллах. Дефекты структуры оказывают существенное, порой определяющее, влияние на свойства твердых тел. Такими структурно-чувствительными (т. е. зависящими от дефектов структуры) свойствами являются электропроводность, фотопроводимость, прочность и пластичность, окраска кристаллов и т. д. Процессы диффузии, роста кристаллов, рекристаллизации и ряд других можно удовлетворительно объяснить, исходя из предположения об их зависимости от дефектов. В настоящее время основные сведения о дефектах необходимы не только физикам, но также конструкторам и создателям приборов на основе твердых тел, занимающимся выращиванием совершенных монокристаллов. 5.1 Классификация дефектов в кристаллах Классификацию дефектов обычно осуществляют по чисто геометрическим признакам, а именно по числу измерений, в которых нарушения структуры кристалла простираются на расстояния, превышающие характерный параметр решетки. Выделяют четыре класса дефектов. 1. Точечные (нульмерные) дефекты. Само их название свидетельствует о том, что нарушения структуры локализованы в отдельных точках кристалла. Размеры указанных дефектов во всех трех измерениях не превышают одного или нескольких межатомных расстояний. К точечным дефектам относят вакансии (вакантные узлы кристаллической решетки), атомы в междоузлиях, атомы примесей в узлах или междоузлиях, а также сочетания примесь - вакансия, примесь - примесь, двойные и тройные вакансии. Точечные дефекты могут появиться в твердых телах вследствие нагревания (тепловые дефекты), облучения быстрыми частицами (радиационные дефекты), отклонения состава химических соединений от стехиометрии (стехиометрические дефекты), пластической деформации. 2. Линейные (одномерные) дефекты характеризуются тем, что нарушения периодичности простираются в одном измерении на расстояния, много большие параметра решетки, тогда как в двух других измерениях они не превышают нескольких параметров. Линейными дефектами являются дислокации, микротрещины. Дислокации возникают в результате пластической деформации кристалла в процессе роста или при последующих обработках. Возможно также образование неустойчивых линейных дефектов из цепочек точечных дефектов. 3. Поверхностные (двухмерные) дефекты в двух измерениях имеют размеры, во много раз превышающие параметр решетки, а в третьем - несколько параметров. Двухмерные дефекты могут быть следствием наличия примесей в расплаве. Границы зерен и двойников, дефекты упаковки, межфазные границы, стенки доменов, а также поверхность кристалла представляют собой двухмерные дефекты. 4. Объемные (трехмерные) дефекты - это микропустоты и включения другой фазы. Они возникают обычно при выращивании кристаллов или в результате некоторых воздействий на кристалл. Так, например, наличие большого количества примесей в расплаве, из которого ведется кристаллизация, может привести к выпадению крупных частиц второй фазы. 5.2 Точечные дефекты в кристаллах Наиболее распространенными точечными дефектами являются энергетические дефекты - фононы - временные искажения регулярности решетки кристалла, вызванные тепловым движением. К энергетическим дефектам кристаллов относятся также временные несовершенства решетки (возбужденные состояния), вызываемые воздействием различных радиаций: света, рентгеновского или γ-излучения, α-излучения, потока нейтронов. К  электронным дефектам относятся избыточные электроны, недостаток электронов (незаполненные валентные связи в кристалле - дырки) и экситоны. Последние представляют собой парные дефекты, состоящие из электрона и дырки, которые связаны кулоновскими силами. К атомным дефектам относятся примеси, дефекты Френкеля и дефекты Шотки. Примеси имеются в кристаллической решетке всегда, поскольку современные методы очистки кристаллов не позволяют получать кристаллы с содержанием примесных атомов менее 1011 см-3. Е 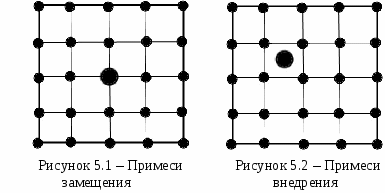 сли атом примеси замещает атом основного вещества в узле решетки, он называется примесью замещения (см. рисунок 5.1). Если примесный атом внедряется в междоузлие, его называют примесью внедрения (см. рисунок 5.2). Хотя относительная концентрация атомных дефектов может быть небольшой, но изменения физических свойств кристалла, вызванные ими, могут быть огромными. Атомные дефекты могут влиять на механические, электрические, магнитные и оптические свойства кристаллов. В качестве иллюстрации приведем лишь один пример: тысячные доли процента некоторых примесей к чистым полупроводниковым кристаллам изменяют их электрическое сопротивление в 105-106 раз. Механизм возникновения точечных дефектов впервые был предложен Я. И. Френкелем. Введенные им представления просты и наглядны. В физике хорошо известно явление сублимации - испарения твердых тел. Над поверхностью твердых тел, так же как и над поверхностью жидкости, всегда существует «пар», состоящий из атомов данного вещества. Атомы, образующие поверхностный слой кристалла, могут вследствие нагревания приобретать кинетическую энергию, достаточную для того, чтобы оторваться от поверхности и перейти в окружающее пространство. Я. И. Френкель предположил, что такой отрыв может иметь место не только для поверхностных атомов, но и для атомов внутри кристалла. Действительно, согласно основным принципам статистической физики, даже в том случае, когда средняя кинетическая энергия атомов очень мала, в кристалле всегда найдется некоторое количество атомов, кинетическая энергия которых может быть очень велика. При этом в соответствии с вероятностным характером этого явления любой атом кристалла в тот или иной момент времени может приобрести энергию, значительно большую, чем средняя кинетическая энергия атомов кристалла. Такой атом может выйти из своего равновесного положения, т. е. из узла решетки. Перемещаясь по кристаллу и передавая энергию остальным атомам, он занимает новое равновесное положение. Если все ближайшие узлы решетки заняты, то он может разместиться только в междоузлии. Оставшийся пустым узел решетки получил название вакансии. Точечные дефекты в виде совокупности атомов в междоузлиях и вакансий называют дефектами по Френкелю (см. рисунок 5.3). Парные дефекты Френкеля возникают легче в кристаллах, содержащих большие межатомные промежутки, чем в плотноупакованных. В последних для междоузельных атомов нет места. Примером кристаллов первого типа являются кристаллы со структурой алмаза и каменной соли, а кристаллов второго типа - металлы с плотной упаковкой. Так, например, маловероятно встретить при обычных условиях междоузельные атомы в гранецентрированных металлах. К 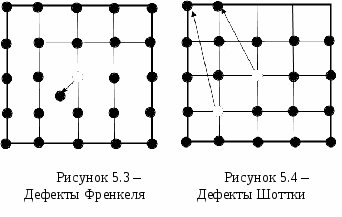 роме парных дефектов по Френкелю, в кристаллах имеются и одиночные точечные дефекты - вакансии, впервые рассмотренные В. Шоттки (см. рисунок 5.4). Дефекты по Шоттки обычно встречаются в кристаллах с плотной упаковкой атомов, где образование междоузельных атомов затруднено и энергетически не выгодно. Процесс образования дефектов в таком кристалле может происходить следующим образом. Некоторые атомы из приповерхностного слоя в результате теплового движения могут выйти из кристалла на поверхность. Образовавшаяся вакансия мигрирует затем в объем кристалла. Образование дефектов по Шоттки уменьшает плотность кристалла из-за увеличения его объема при постоянной массе. При образовании дефектов по Френкелю плотность остается неизменной, так как объем кристалла не изменяется. Точечные дефекты типа вакансий имеются в каждом кристалле, как бы тщательно он ни выращивался. Более того, в реальном кристалле вакансии постоянно зарождаются и исчезают под действием тепловых флуктуаций. По формуле Больцмана равновесная концентрация вакансий nв в кристалле при данной температуре (Т) определится так:  ,где п - число атомов в единице объема кристалла, е - основание натуральных логарифмов, k- постоянная Больцмана, ЕВ - энергия образования вакансий. Для большинства кристаллов энергия образования вакансий примерно равна 1 эв, при комнатной температуре kT0,025 эв, следовательно,  .При повышении температуры относительная концентрация вакансий довольно быстро растет: при Т = 600° К она достигает 10-5, а при 900° К - 10-2. Аналогичные рассуждения можно сделать относительно концентрации дефектов по Френкелю, с учетом того, что энергия образования внедрений значительно больше энергии образования вакансии. 5.3 Дислокации К линейным дефектам кристаллической решетки относятся дислокации. Простейшими видами дислокаций являются краевая и винтовая дислокации. Об их характере можно судить по рисунку 5.5. На рисунке 5.5 а изображено строение идеального кристалла в виде семейства параллельных друг другу атомных плоскостей. Если одна из этих плоскостей обрывается внутри кристалла (см. рисунок 5.5 б), то место обрыва ее образует краевую дислокацию. В случае винтовой дислокации (см. рисунок 5.5 в) характер смещения атомных плоскостей иной. Здесь нет обрыва внутри кристалла какой-нибудь из атомных плоскостей, но сами атомные плоскости представляют собой систему, подобную винтовой лестнице. По существу, это одна а 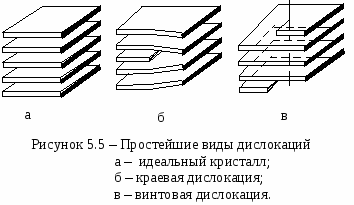 томная плоскость, закрученная по винтовой линии. Если обходить по этой плоскости вокруг оси винтовой дислокации, то с каждым оборотом будем подниматься или опускаться на один шаг винта, равный межплоскостному расстоянию. Любая конкретная дислокация может быть представлена как сочетание краевой и винтовой дислокаций. Дислокации, являясь протяженными дефектами кристалла, охватывают своим упругим полем искаженной решетки гораздо большее число узлов, чем атомные дефекты. Ширина дислокации составляет всего несколько периодов решетки, а ее длина достигает многих тысяч периодов. Энергия дислокаций оценивается величиной порядка 410-19 Джна 1 мдлины дислокации. Энергия дислокаций, рассчитанная на одно межатомное расстояние вдоль длины дислокации, для разных кристаллов лежит в пределах от 3 до 30 Эв. Такая большая энергия, необходимая для создания дислокаций, является причиной того, что число их практически не зависит от температуры. В отличие от вакансий, вероятность возникновения дислокаций за счет флуктуации теплового движения пренебрежимо мала для всего интервала температур, в котором возможно кристаллическое состояние. В недеформированных металлических кристаллах через площадку в 1 см2проходит 106 - 108 дислокаций, при пластической деформации плотность дислокаций возрастает в тысячи, а иногда и в миллионы раз. Важнейшим свойством дислокаций является их легкая подвижность и активное взаимодействие между собой и с любыми другими дефектами решетки. Для того, чтобы вызвать движение дислокации, достаточно создать в кристалле напряжение сдвига порядка 10 Н/мм2.Уже под влиянием такого небольшого напряжения дислокация будет перемещаться в кристалле, пока не встретит какого-либо препятствия, которым может быть граница зерна, другая дислокация, атом внедрения и т.д. При встрече с препятствием дислокация искривляется, огибает препятствие, образуя расширяющуюся дислокационную петлю, которая затем отшнуровывается и образует отдельную дислокационную петлю. Причем в области обособленной расширяющейся петли остается отрезок линейной дислокации (между двумя препятствиями), который под воздействием внешнего напряжения снова будет изгибаться, и весь процесс повторится снова. Таким образом, при взаимодействии движущихся дислокаций с препятствиями происходит рост числа дислокаций. 5.4 Границы зерен Поликристаллы состоят из большого числа мелких монокристаллических зерен, разделенных некоторыми зонами перехода, получившими название границ зерен. Граница зерна представляет собой поверхность между двумя монокристаллами различной ориентации, примыкающими друг к другу таким образом, что отсутствует нарушение сплошности вещества. Долгое время считалось, что это аморфный слой толщиной в несколько десятков нанометров. Однако к настоящему времени надежно установлено, что ширина области «плохого» материала на границе между зернами не превышает одного - двух межатомных расстояний. Границы с разориентацией соседних зерен менее 10° относятся к малоугловым, а с большей разориентацией - к высокоугловым. Все субзеренные границы состоят из дислокаций. Малоугловые границы возникают при росте кристаллов из расплава и при пластической деформации. Малоугловая граница притягивает к себе точечные дефекты, в том числе и примесные атомы, вследствие упругого взаимодействия с ними дислокаций, составляющих границу. Примесные атомы тормозят миграцию малоугловых границ, стабилизируя субструктуру. Границы зерен, выросших из разных центров при кристаллизации и фазовых превращениях в твердом состоянии, чаще всего бывают высокоугловыми. Границы зерен оказывают существенное влияние на многие свойства кристаллов, в частности на электропроводность, поглощение ультразвука, оптические свойства и т. д. Наличие границ приводит к тому, что в поликристаллах коэффициент диффузии примесей значительно больше, чем в монокристаллах. 5.5 Прочность твердых тел Рассмотрим какое влияние оказывают дефекты кристалла на его прочность. Прочность идеального кристалла можно рассчитать как силу, необходимую для того, чтобы оторвать атомы (ионы, молекулы) друг от друга, либо сдвинуть их, преодолев силы межатомного сцепления, т. е. идеальная прочность кристалла должна определяться произведением величины сил межатомной связи на количество атомов, приходящихся на единицу площади соответствующего сечения кристалла. Прочность реальных кристаллов на сдвиг обычно на три - четыре порядка ниже расчетной идеальной прочности (см. таблицу 5.1). Такое большое снижение прочности кристалла нельзя объяснить уменьшением рабочей площади поперечного сечения образца за счет пор, каверн и микротрещин. Таблица 5.1 - Значения скалывающих напряжений некоторых металлов
Причинами столь разительного несоответствия теоретической и практической прочности являются не свойства совершенной кристаллической структуры тела, а наличие в кристалле разного рода несовершенств, дефектов, а также влияние на результаты исследования масштабного фактора при испытании образцов разного объема. Расчеты и опыт показывают, что зависимость между количеством дефектов и прочностью схематически можно представить кривой, изображенной на рисунке. 5.6. 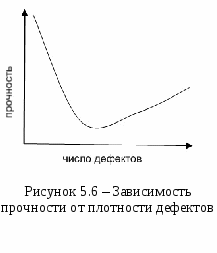 Из рисунка 5.6 видно, что прочность материала высока, когда в нем либо совсем нет дислокаций, либо их очень много. Практически все существующие и разрабатываемые способы упрочнения относятся к правой части этой кривой, т.е. имеют своей целью увеличение плотности дислокаций в металле. Дело в том, что бездислокационный кристалл нужных размеров вырастить практически невозможно. Исключение представляют материалы в виде нитевидных кристаллов. Лекция 6 Механические свойства твердых тел 6.1 Напряжения 6.2 Деформации 6.3 Диаграммы деформаций 6.4 Закон Гука для изотропных твердых тел 6.5 Закон Гука для анизотропных твердых тел Механические свойства твердого тела отражают его реакцию на воздействие некоторых внешних факторов. В простейшем случае такими внешними факторами являются механические воздействия: сжатие, растяжение, изгиб, удар, кручение. Механические свойства определяются, в первую очередь, силами связи, действующими между атомами или молекулами, составляющими твердое тело. 6.1 Напряжения Если тело находится под действием внешних сил, то в каждой его точке возникают механические напряжения. В этом случае говорят, что тело находится в напряженном состоянии. Если в таком теле выделить какой-либо элемент объема, то на него действуют два типа сил: 1) объемные силы (например, сила тяжести), действующие на все элементы тела; их значение пропорционально объему элемента; 2) силы, действующие на поверхность элемента со стороны окружающих его частей тела. Эти силы пропорциональны площади поверхности элемента. Такую силу, отнесенную к единичной площади, называют напряжением. Например, при осевом растяжении изотропного цилиндрического стержня (см. рисунок 6.1) в условиях статического равновесия внешняя сила F уравновешивается внутренней силой сопротивления:  .П 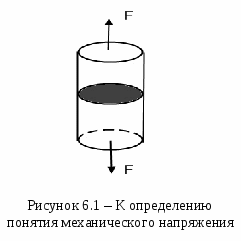 ри описании напряженного состояния будем считать, что напряжение во всем теле однородно, все части тела находятся в равновесии, объемные силы отсутствуют. Выберем любую точку О в объеме этого тела и вокруг нее построим бесконечно малый куб (см. рисунок 6.2). 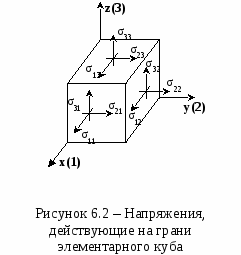 Три взаимно перпендикулярных оси х, у, z, исходящие из этой точки, выберем в качестве прямоугольной системы координат. Поскольку в дальнейшем при написании формул удобнее оперировать цифрами, обозначим ось х цифрой 1, ось у - цифрой 2 и ось z - цифрой 3. Ребра элементарного куба параллельны осям Ox, Оу, Oz. При равновесии силы, действующие на противоположные грани, равны, поэтому достаточно рассмотреть силы, действующие на три взаимно перпендикулярные грани. Каждое из напряжений, действующих на три непараллельные грани куба, раскладываем на одну нормальную составляющую и две касательные, т. е. лежащие в рассматриваемой грани. Обозначим σij компоненту напряжения, действующую в направлении i на грань куба, перпендикулярную оси j. Напряжения σ11, σ22, σ33 - нормальные (растягивающие или сжимающие) напряжения; σ12, σ13, σ23 и т. д. - касательные (скалывающие или сдвиговые) напряжения. Итак, напряженное состояние в точке характеризуется девятью величинами σij, которые являются компонентами тензора второго ранга - тензора механических напряжений: 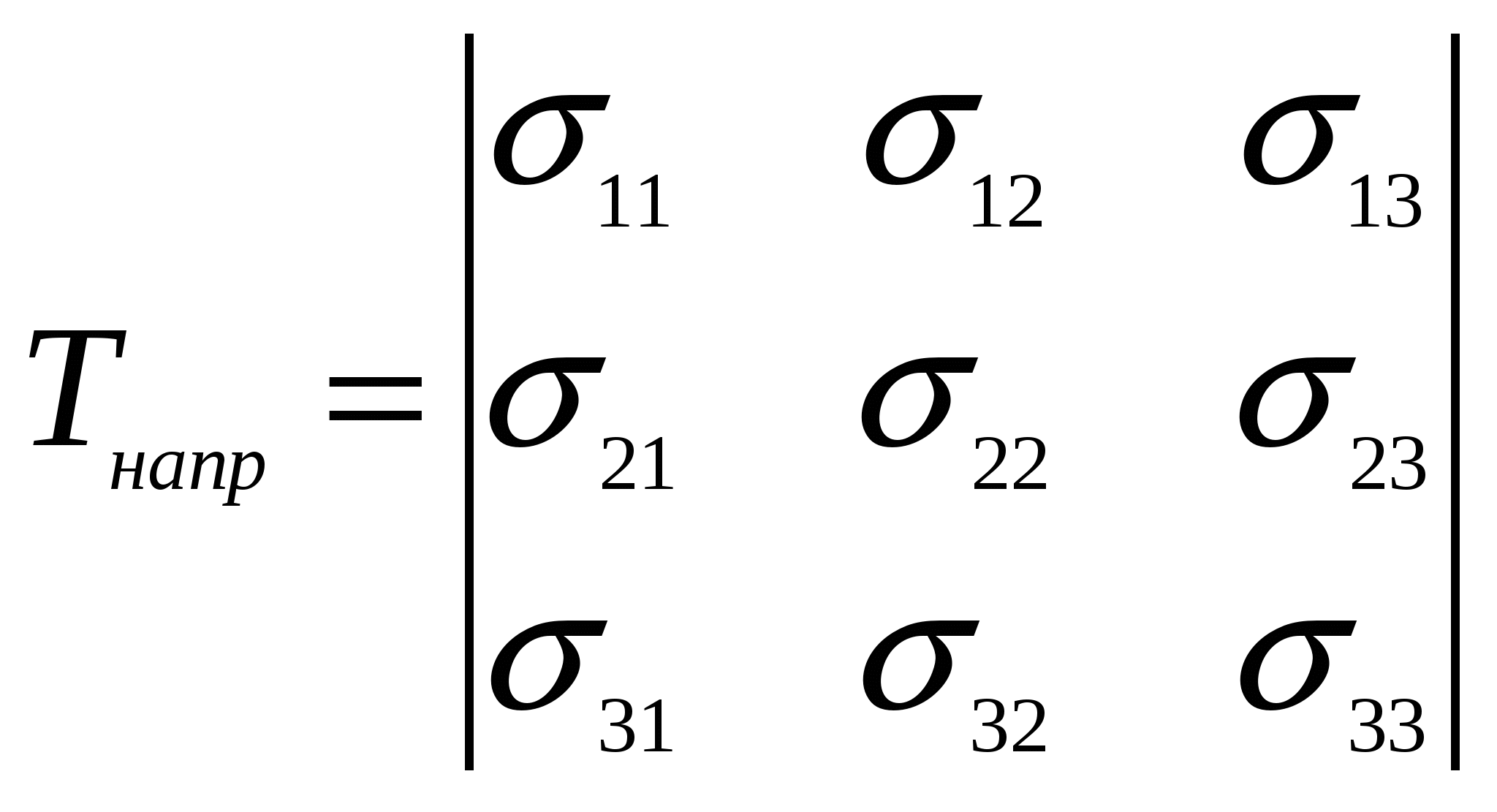 .Так как элементарный куб находится в состоянии равновесия, то можно показать, что σ12 = σ21, σ13 = σ31, σ23 = σ32. Отсюда следует, что из девяти компонент только шесть являются независимыми и тензор оказывается симметричным, т. е. компоненты, симметричные относительно главной диагонали тензора, равны между собой (σij = σji). Напряженное состояние, возникающее в твердом теле, существенно влияет на процессы его деформации и разрушения. Важной характеристикой напряженного состояния является коэффициент «мягкости», равный отношению максимальных касательных напряжений к максимальным нормальным. Чем меньше этот коэффициент, тем «жестче» напряженное состояние. Касательные напряжения способствуют развитию пластической деформации, а нормальные - разрыву межатомных связей, хрупкому разрушению твердого тела. 6.2 Деформации Деформация - изменение объема или формы твердого тела без изменения его массы под действием внешней силы. Деформация - это процесс, при котором изменяется расстояние между какими-либо точками тела. Простейшие виды деформации: растяжение, сжатие, сдвиг, кручение, изгиб. Элементарной деформацией при одноосном растяжении цилиндрического образца является удлинение. При приложении растягивающей силы образец увеличивается в длине и уменьшается в диаметре. Обычно деформацию выражают в относительных единицах. Так, если образец имел начальную длину l0 и lk после приложения растягивающей силы (см.рисунок 6.3), то относительная деформация образца  .Д 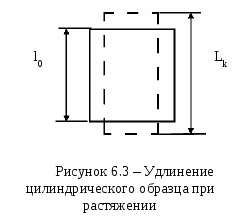 ля полного описания деформированного состояния кроме удлинений (укорочений) необходимо знать сдвиги, возникающие под действием касательных напряжений. При механических испытаниях принято характеризовать деформации относительным изменением линейных размеров образцов, а также углом сдвига, т. е. углом, на который изменился первоначальный прямой угол элемента поверхности деформируемого тела или образца. Относительным сдвигом называют тангенс угла сдвига (см. рисунок 6.4): 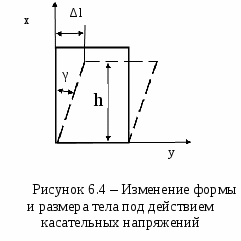  .Любая деформация может быть представлена в виде определенной комбинации сдвигов и удлинений. В общем случае деформированное состояние в выбранной точке характеризуется девятью величинами εij, которые являются компонентами тензора второго ранга - тензора деформаций: 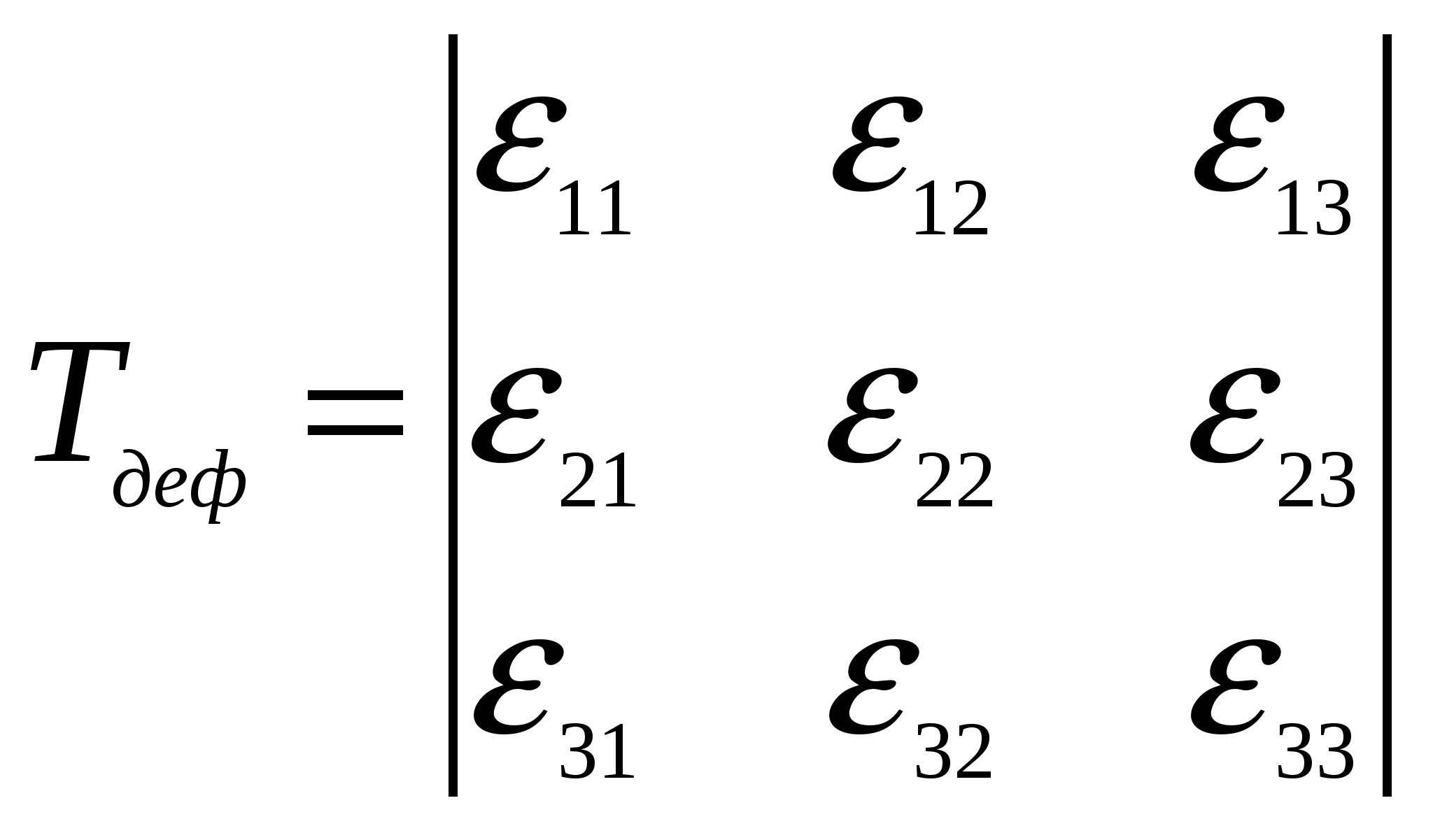 .Р 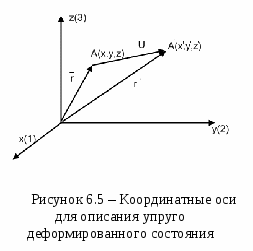 ассматривая случай объемной деформации твердого тела, выберем в качестве осей координат три ортогональные оси х, у, z с началом в точке О (см. рисунок 6.5). Пусть точка О после деформации осталась на месте, а все остальные точки тела изменили свои положения. Определим положение точки А (х, у, z) до деформации радиус-вектором  . После деформации точка А (х, у, z) переместится в положение А' (х', у', z'), определяемое радиусом-вектором  . Вектор  называется вектором смещения,  - компоненты вектора смещения по осям x, y, z.Компоненты вектора смещения связаны с компонентами тензора деформаций соотношениями Коши:  ,  ,  , , , .Компоненты  ,  ,  задают относительное удлинение вдоль соответствующих осей, а компоненты  ,  ,  задают изменения углов, вызванные приложением нагрузки.6.3 Диаграммы деформаций Механические свойства твердых тел наиболее полно описываются диаграммами деформации. Диаграммы деформации представляют собой зависимости между механическими напряжениями, которые возникают в твердом теле при приложении к нему внешней силы, и деформациями. Из диаграмм деформации получают систему характеристик прочности (пределы прочности, текучести, упругости, относительные удлинения, сужения и др.). Н 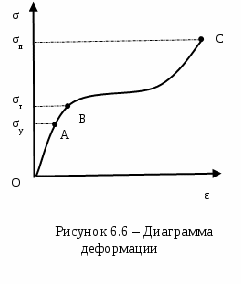 а рисунке 6.6 приведена типичная диаграмма деформации для одноосного растяжения цилиндрического образца. Как видно из рисунка 6.6, кривая ОС обнаруживает несколько характерных особенностей. Так, при малых напряжениях наблюдается линейная зависимость деформации от напряжения (участок OA). Другой особенностью участка OA является то, что после снятия нагрузки форма и размеры образца восстанавливаются, т. е. деформация оказывается обратимой. Обратимость деформации на участке OA наблюдается только в том случае, если нагрузка прилагается и снимается сравнительно быстро. Если нагрузка приложена в течение большого промежутка времени, то мы сталкиваемся с явлением «крипа» (ползучести), а следовательно, и с необратимостью деформации. Прямолинейный участок OA называют областью упругой деформации. За пределами упругой области при переходе через точку А (напряжение, соответствующее этой точке, называют пределом упругости σу) кривая переходит в так называемую пластическую область. Величина σт соответствует пределу текучести минимальному напряжению, при котором деформация продолжает возрастать без увеличения нагрузки. Точка С кривой соответствует пределу прочности σп. При достижении предела прочности образец разрушается. 6.4 Закон Гука для изотропных твердых тел Основные закономерности поведения твердых тел в упругой области экспериментально впервые были изучены Р. Гуком. Им установлено, что при нагружении изотропного тела, когда деформации и напряжения достаточно малы, деформация пропорциональна приложенному напряжению (закон Гука):  Здесь  - продольная деформация при растяжении; S - константа упругой податливости, или просто податливость;  - напряжения.Закон Гука можно записать и в такой форме:  ,где  - константа упругой жесткости, или просто жесткость. В литературе, особенно технической, часто называют модулем Юнга и обозначают  , тогда .Закон Гука для сдвиговой деформации при действии касательных (скалывающих) напряжений имеет такой же простое вид, как и для случая растяжения:  .где  - модуль сдвига (или модуль упругости при сдвиге),  - тангенс угла сдвига. Закон Гука в приведенной выше форме определяет зависимость между напряжением и деформацией в одном и том же направлении, т. е. в направлении приложения внешней силы. Такая запись носит название элементарного закона Гука. Однако деформация может возникать и в направлениях, отличных от направления приложения силы. В этих случаях закон Гука в элементарной форме уже недостаточен и необходимо воспользоваться обобщенным законом Гука. В самом деле, при одноосном растяжении цилиндрического образца происходит не только его удлинение в направлении приложенной силы, но и сжатие образца в поперечных направлениях, т. е. имеет место трехмерная деформация. Поперечная деформация при упругом растяжении или сжатии характеризуется коэффициентом Пуассона  , равным отношению изменения размеров в поперечном направлении к их изменению в продольном направлении. Для большинства твердых тел значения лежат между 0,25 и 0,35.Обобщенный закон Гука устанавливает линейную зависимость не только между одним напряжением и соответствующей деформацией, а между всеми компонентами тензора напряжений и компонентами тензора деформации. Обобщенный закон Гука для изотропного тела записывают в следующем виде:  , , , , , .Константы упругости связаны между собой выражением  .Таким образом, зная две константы, можно всегда определить третью. 6.5 Закон Гука для анизотропных твердых тел Монокристаллические твердые тела являются телами анизотропными. В общем случае для монокристаллов любые произвольно выбранные направления по свойствам неэквивалентны. Как уже отмечалось, напряжения и деформации описываются тензорами второго ранга, каждый из которых определяется девятью компонентами. Если деформация бесконечно мала и однородна, то каждая компонента тензора деформации линейно связана со всеми компонентами тензора напряжений и, наоборот, каждая компонента тензора напряжения линейно связана со всеми компонентами тензора деформаций. В этом заключается сущность закона Гука для анизотропных твердых тел. Математический закон Гука для монокристаллов запишется в виде  ,либо как  ,где  и  - константы податливости и жесткости кристалла соответственно. Всего будет 81 компонента  и 81 компонента  .Величины и образуют тензор четвертого ранга. Тензор, составленный из коэффициентов , называют тензором упругой жесткости или просто тензором упругости. Тензор, составленный из коэффициентов , называют тензором упругой податливости.Так как тензоры деформации и напряжения являются симметричными тензорами второго ранга (  и  ), то независимых компонент и будет уже не 81, а только 36, поскольку в этом случае , , , .Для кристаллов тензоры упругих модулей, каждый из которых составлен из 36 компонент, в свою очередь также являются симметричными, т. е. компоненты и симметричны и относительно перестановки пар индексов: ,.Наличие таких равенств приводит к тому, что в общем случае число независимых компонент тензоров упругих модулей сокращается с 36 до 21 - столько констант имеет твердое тело, не обладающее никакой симметрией. При решении многих конкретных задач для упругих модулей полезна запись в матричных обозначениях, поскольку она уменьшает число индексов у компонентов. При матричной записи двойное сочетание ij=m и kl=n заменяется одним индексом от 1 до 6 по следующей схеме: 11 - 1; 22 - 2; 33 - 3; 23, 32 - 4; 31, 13 -5; 12, 21 - 6. Коэффициенты упругой жесткости и упругой податливости можно представить в виде таблиц: 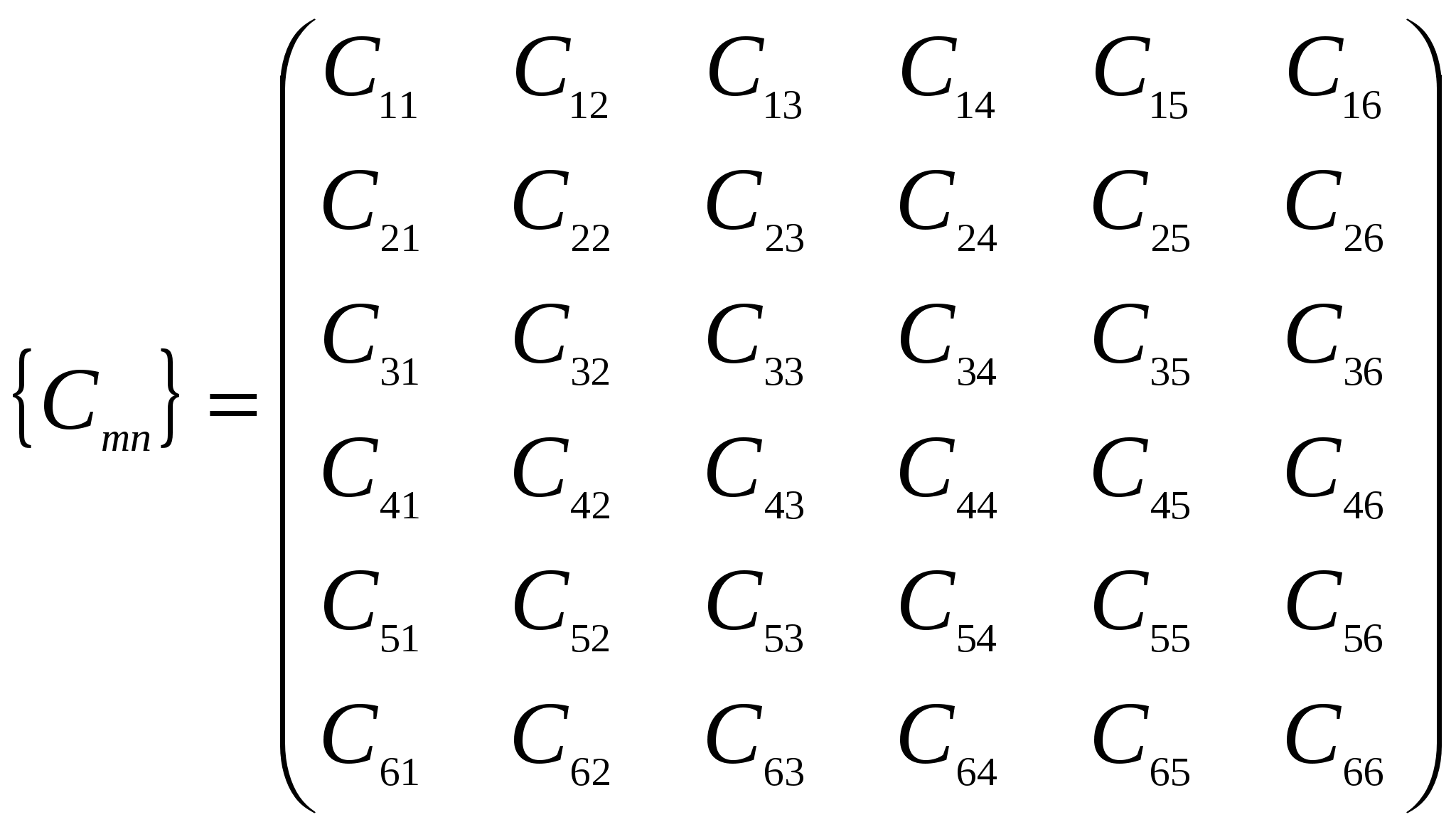 , 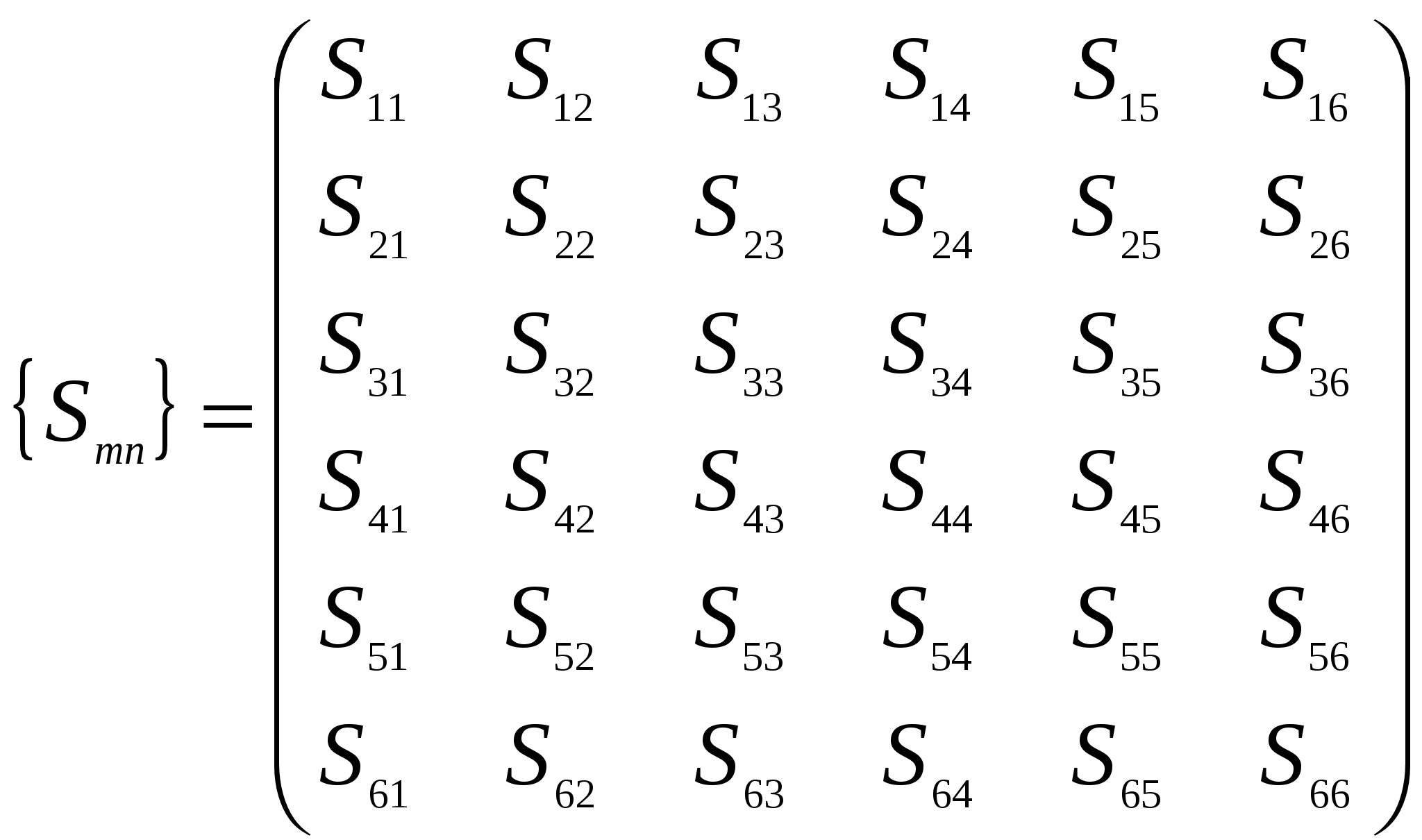.Полное число упругих констант сокращается в зависимости от симметрии кристалла. Так, если кристалл обладает триклинной симметрией, то полное число упругих констант равно 21, а для кристаллов кубической симметрии оно равно 3. Основное свойство кубического кристалла состоит в том, что направления ±х, ±y, ±z взаимно перпендикулярны и полностью эквивалентны. Это приводит к тому, что для кубических кристаллов имеется лишь три независимые компоненты и набор постоянных упругой жесткости сводится к матрице: 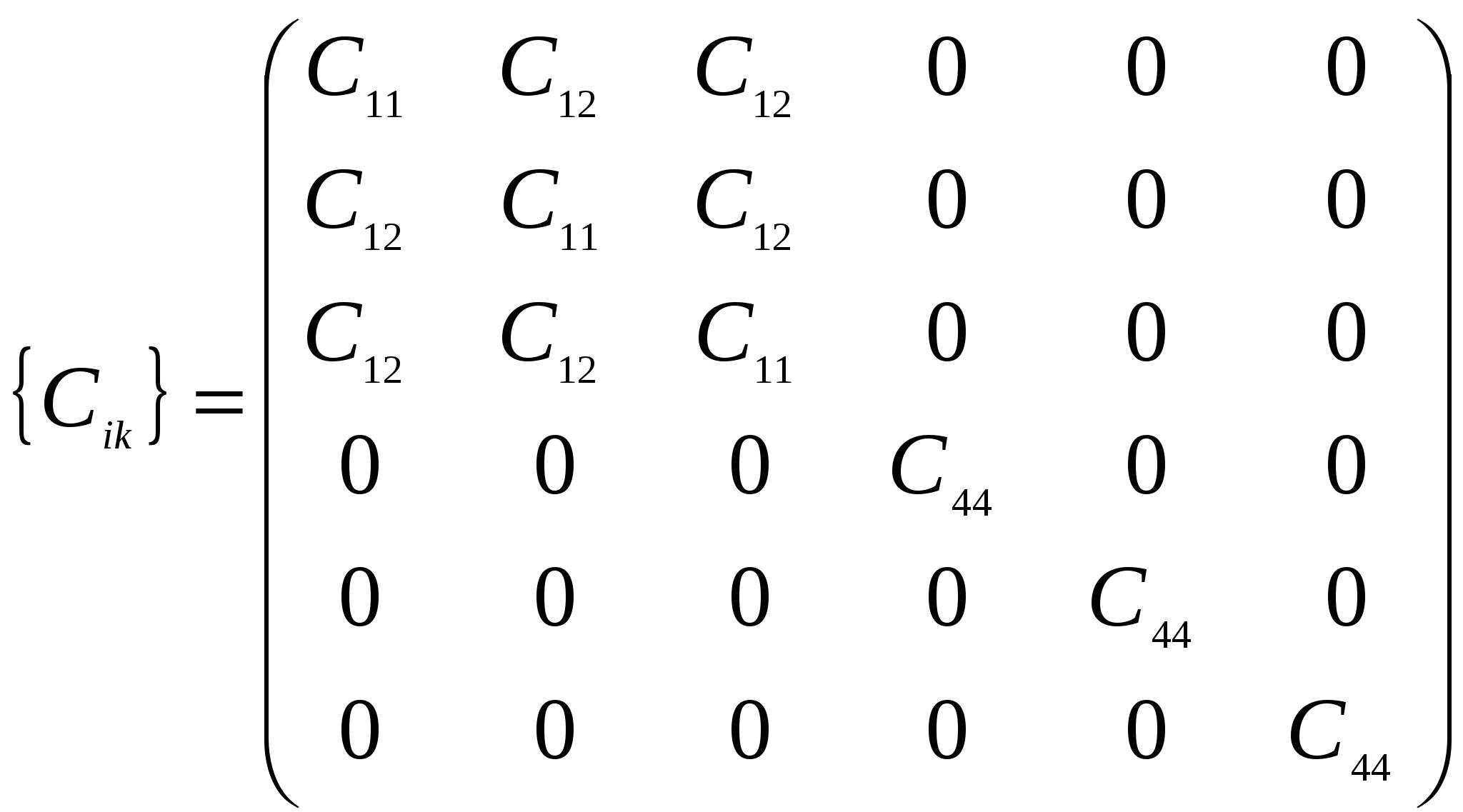 .Однако, если образец кубического кристалла вырезан в каком-либо направлении, отличающемся даже на малый угол от основных кристаллографических направлений, то он общем случае приобретает свойства кристаллов триклинной системы. Лекция 7 | |||||||||||||||||||||||||||||||||||||||||||||