Физика твердого тела (тексты лекций). Гомельский государственный университет имени Франциска Скорины С. А. Хахомов, А. В. Семченко, Ю. В. Никитюк физика твердого тела
 Скачать 1.46 Mb. Скачать 1.46 Mb.
|
Плотность упаковкиСмоделируем частицы в узлах кристаллической решетки в виде идеальных (не деформированных) соприкасающихся шаров. Тогда плотность упаковки (коэффициент упаковки или компактность данной решетки) представляет собой отношение объема, занимаемого шарами в элементарной ячейке, ко всему объему самой элементарной ячейки. В качестве примера рассмотрим примитивную кубическую ячейку (см. рисунок 2.8) Пусть радиус шара r. Тогда длина ребра куба 2r. Объем одного шара 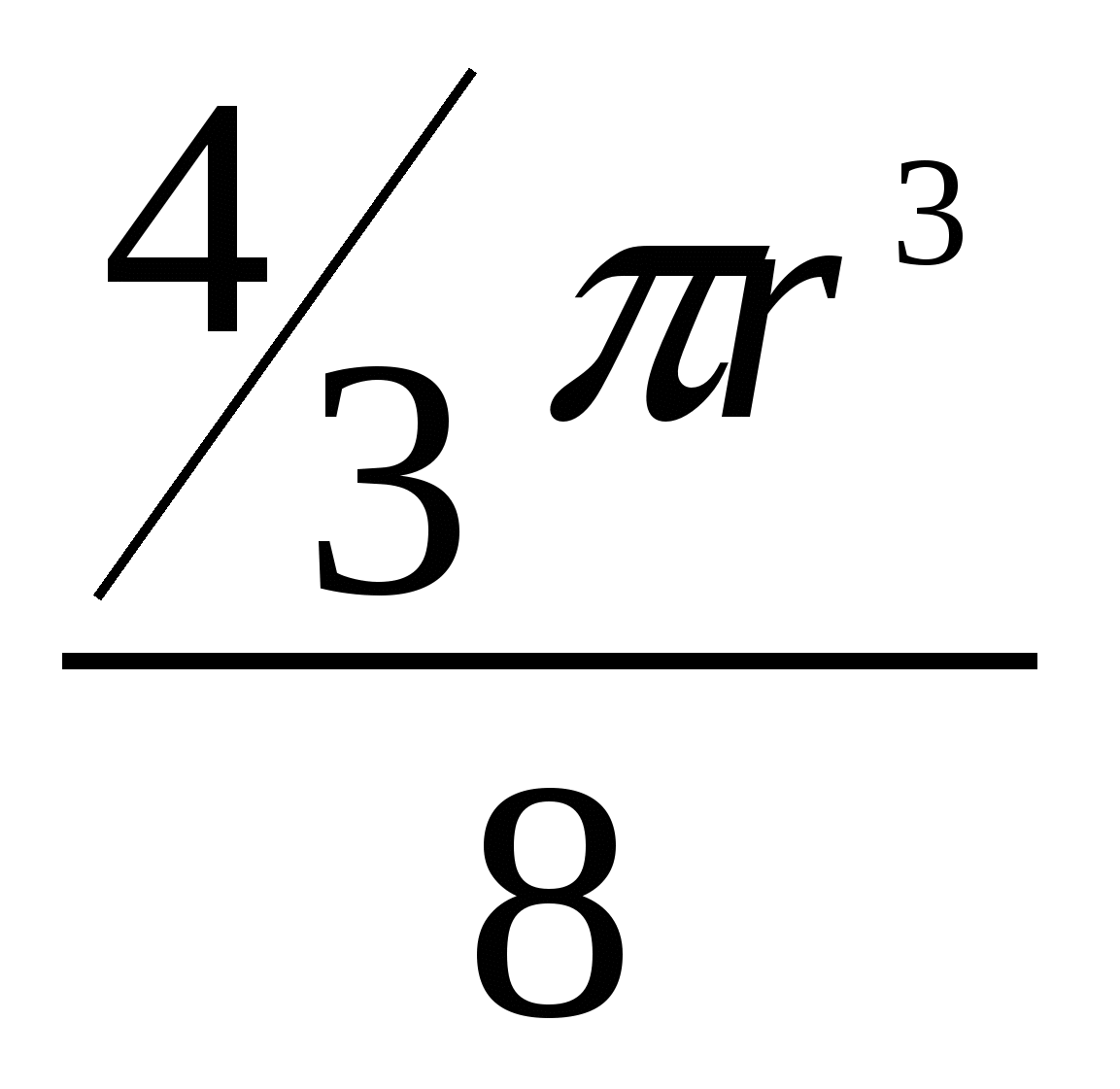 . Таких шаров 8, и каждый принадлежит ячейке на 1/8. Тогда объем занимаемый шарами внутри ячейки: . Таких шаров 8, и каждый принадлежит ячейке на 1/8. Тогда объем занимаемый шарами внутри ячейки:И плотность упаковки: f = 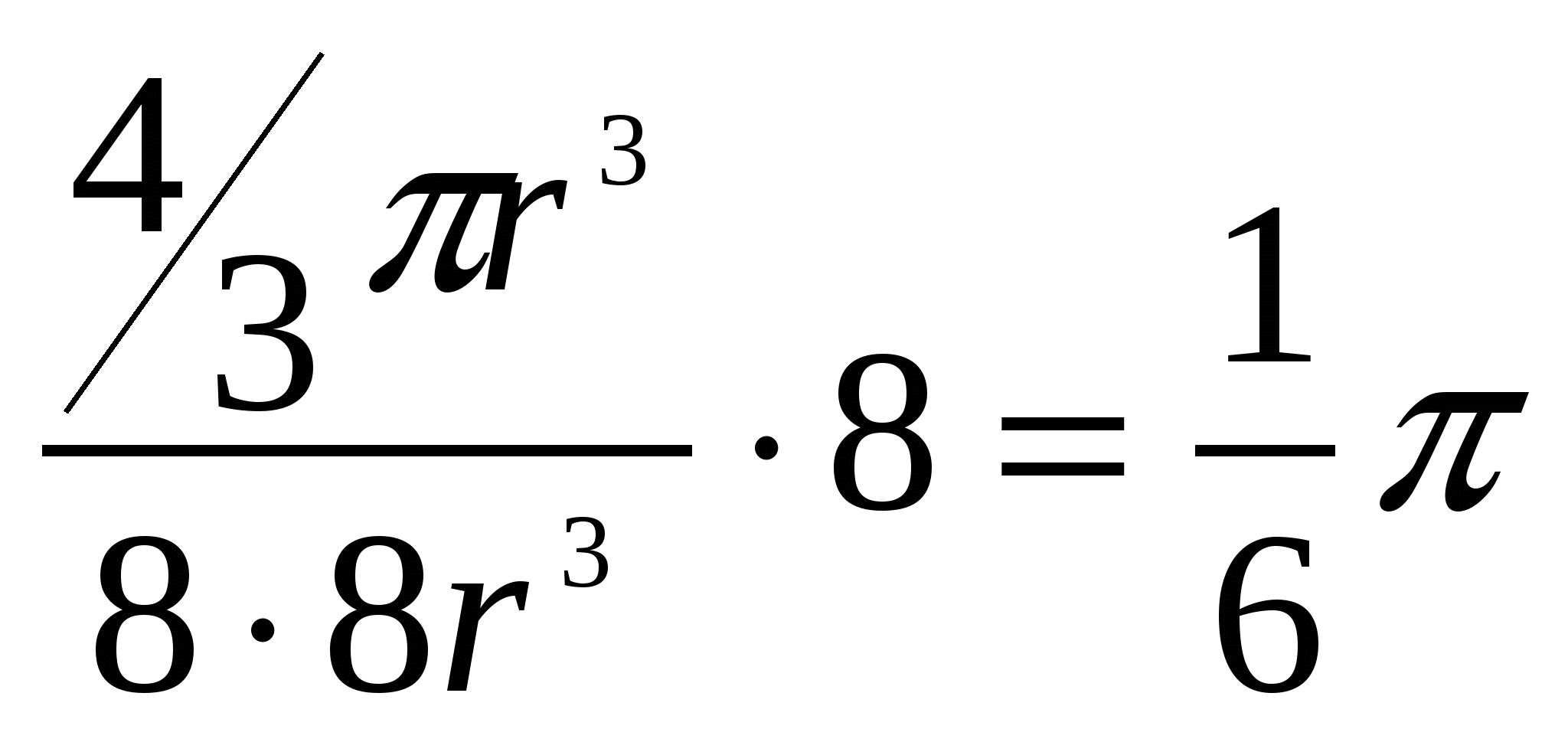 =0,52. =0,52. 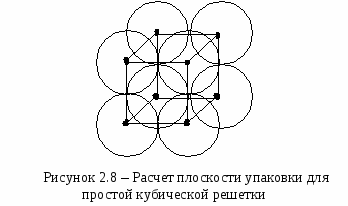 2.4 Анизотропия кристаллов Физические свойства твердого тела можно разделить на две категории: одна из них включает такие свойства, как плотность, удельная теплоемкость, которые не связаны с выбором какого-либо направления внутри твердого тела, свойства же другой категории (механические модули, термический коэффициент расширения, коэффициент теплопроводности, удельное сопротивление, показатель преломления и др.) могут быть различными для разных направлений в твердом теле. Изотропностью называется независимость физических свойств тела от направления внутри него. Если такие физические свойства тела как модуль упругости, коэффициент теплопроводности, показатель преломления и т. п., одинаковы по всем направлениям, то такое тело будет изотропным. Под анизотропией понимается зависимость свойств макроскопически однородного тела от направления. Изотропными являются аморфные тела, жидкости и газы. Анизотропия же является характерной особенностью кристаллов. Но обнаружить анизотропность можно не у всяких кристаллических тел, а только у монокристаллов. Большинство окружающих нас кристаллических тел, например, металлы, являются поликристаллическими, т. е. они состоят из очень большого числа сросшихся друг с другом мелких кристаллических зерен, ориентированных различным образом. Если в ориентации этих мелких кристалликов нет какого-либо определенного порядка, то данное поликристаллическое тело будет изотропно. Если же в ориентации кристаллических зерен наблюдается упорядоченность (а она может возникнуть при таких методах обработки металлов, как прокатка, протяжка, волочение), то материал называется текстурированным и обнаруживает некоторую анизотропность. В обычных поликристаллических металлах кристаллические зерна настолько малы, что, как правило, различимы лишь при наблюдении в микроскоп. Но при медленном охлаждении расплава металла можно получить крупнозернистый слиток, в котором кристаллические зерна легко рассмотреть невооруженным глазом. Если же применить особую методику охлаждения расплава металла, то можно получить такие образцы, в которых будет находиться всего одно кристаллическое зерно - один кристалл. Такие однокристальные образцы называются монокристаллами. В природе встречаются довольно большие монокристаллы минералов, а иногда и металлов (самородки золота). Можно получить монокристаллы многих веществ (в том числе и металлов) искусственно. Для этого приходится соблюдать иногда очень тонкую и достаточно сложную технологию. Наглядным примером анизотропии механической прочности кристалла является способность кристаллов слюды легко расщепляться на тонкие листочки по определенному направлению и обладать достаточной прочностью в перпендикулярном направлении. Монокристаллы некоторых металлов (цинка, висмута, сурьмы) тоже довольно легко скалываются по определенным плоскостям. Плоскость скола при этом представляет собой хорошее зеркало. Исследования показали, что кристаллы могут обладать анизотропией теплопроводности, электропроводности, магнитных свойств и пр. Анизотропия проявляется и в поверхностных свойствах кристаллов. Например, коэффициент поверхностного натяжения для разнородных граней кристалла имеет различную величину. При росте кристалла из расплава или раствора это является причиной различия скоростей роста разных граней. Анизотропия скоростей роста обусловливает правильную форму растущего кристалла. Анизотропия поверхностных свойств проявляется в различии скоростей растворения разных граней кристалла, адсорбционной способности, химической активности разных граней одного и того же кристалла. Причина анизотропии состоит в том, что кристаллы имеют строго упорядоченное строение. Важнейшим следствием упорядоченной структуры является анизотропия физических свойств кристалла. Поясним сказанное. На рисунке 2.9 изображена схема расположения атомов в кристалле. Плоскость рисунка совпадает с одной из плоскостей, проходящей через узлы кристаллической решетки. Можно сказать, что кристалл представляет собой пачку таких плоскостей, лежащих как листы бумаги в книге. Если произвести сечение такого кристалла плоскостями, перпендикулярными плоскости чертежа, то в зависимости от ориентации плоскостей сечения густота расположения атомов на них будет различной. На рисунке 2.9 направления секущих плоскостей изображены сплошными линиями. Из рисунка хорошо видно, что плотность «населения» плоскостей атомами различна; если расположить эти плоскости в порядке убывания поверхностной плотности атомов, то получится следующий ряд: (010) (100) (110) (120) (320). Вместе с тем видно, что расстояния между смежными секущими плоскостями тем больше, чем плотнее «населенность» их атомами. Легко представить себе, что в наиболее плотно заполненных плоскостях атомы прочнее связаны друг с другом, так как расстояния между ними меньше. С 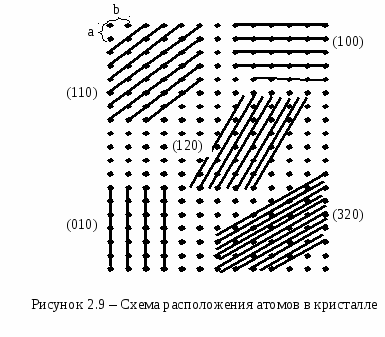 другой стороны, наиболее плотно заполненные плоскости, будучи удаленными друг от друга на относительно большие расстояния, чем мало заселенные плоскости, будут слабее связаны друг с другом. Следовательно, наш условный кристалл обладает анизотропией механической прочности: легче всего его расколоть по плоскости (010). На основании изложенного можно сделать обобщение, что и другие физические свойства кристалла (тепловые, электрические, магнитные, оптические) могут быть различными по разным направлениям. Численные значения некоторых физических свойств кристаллов для разных направлений могут иногда различаться на несколько порядков. У кристаллов графита, например, удельное электрическое сопротивление по направлению [001] почти в сто раз больше, чем по перпендикулярному направлению. Один и тот же кристалл может быть изотропным в отношении одного свойства и анизотропным в отношении другого. Например, кристалл поваренной соли изотропен относительно диэлектрической проницаемости, коэффициента теплового расширения, показателя преломления, но анизотропен в отношении механических свойств и в отношении скоростей роста и растворения граней. Анизотропия физических свойств кристаллов используется в технике, базирующейся на применении монокристаллов (полупроводниковая электроника, электро- и радиотехника, кристаллооптика и др.). Монокристаллические элементы полупроводниковых приборов, стабилизаторов частоты, пьезодатчиков, оптических приборов изготовляются со строгим учетом кристаллографического направления. Для этих целей нужно изготовить монокристаллический образец не только определенной чистоты, формы и размеров, но и с нужной ориентацией кристаллографических осей. Лекция 3 Электронная структура твердых тел 3.1 Классификация состояний электронов в атоме 3.2 Периодическая система элементов Менделеева 3.1 Классификация состояний электронов в атоме Состояние электрона в атоме определяется четырьмя квантовыми числами: главным n, орбитальным l, магнитным ml и спиновым ms. Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы: n=1, 2, 3,… Для атома водорода главное квантовое число определяет энергию атома в стационарном состоянии E(n): E(n)= R/n2, где R=13,6 эВ - универсальная постоянная Ридберга. Состояние электрона в атоме водорода описывается волновой функцией ψ, удовлетворяющей стационарному уравнению Шредингера где Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze(для атома водорода Z=1), имеет следующий вид: где r- расстояние между электроном и ядром. Решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней Самый нижний уровень E1, отвечающий минимальной возможной энергии - основной, все остальные - возбужденные (En> E1). При E<0 движение электрона является связанным - он находится внутри гиперболической потенциальной ямы. И 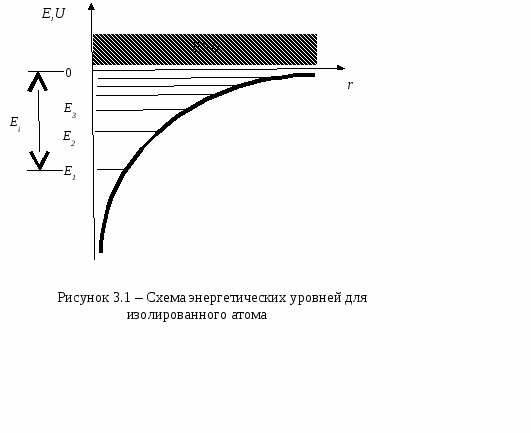 з рисунка 3.1 следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n=∞ Е∞=0. При E>0 движение электрона является свободным; область непрерывного спектра E>0 (заштрихована на рисунке 3.1) соответствует ионизированному атому. Энергия ионизации атома водорода Орбитальное квантовое число l определяет орбитальный момент количества движения электрона pl: Квантовое число l может принимать лишь следующий ряд целочисленных значений: l=0,1,2,…(n-1); всего n значений. Магнитное квантовое число ml определяет ориентацию орбитального момента количества движения plотносительно избранного направленияН (см. рисунок 3.2). Вектор plможет ориентироваться относительно направления Н лишь так, что его проекция на это направление кратна ħ: plН = mlħ. Числоml может принимать следующий ряд дискретных значений (всего 2l+1 значений): ml= -l, -(l-1), …, 0,1,2,…,l. Спиновое квантовое число ms определяет ориентацию собственного момента количества движения электрона (см. рисунок 3.3) относительно избранного направленияН. Вектор psможет ориентироваться относительно направления Н лишь так, что его проекция на это направление равна (ms может принимать лишь два значения: 1/2 и -1/2.): psН = msħ. 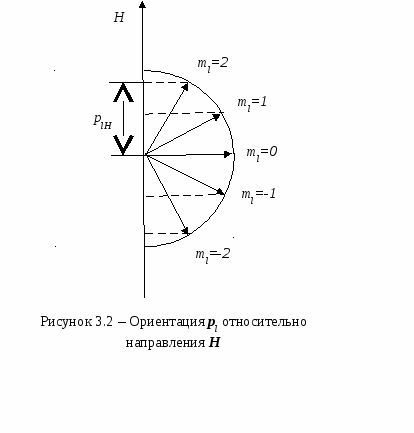 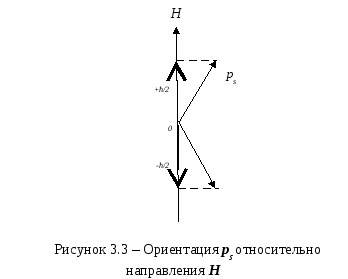 Поскольку при движении электрона в атоме существенны волновые свойства электрона, квантовая механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определят вероятность обнаружения электрона в единице объема. Вероятность обнаружить электрон в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа nи lхарактеризуют размер и форму электронного облака, а квантовое число mlхарактеризует ориентацию облака в пространстве. Состояние электрона, характеризующееся квантовыми числами l=0, называют s-состоянием, l=1 - р-состоянием, l=2 - d-состоянием, l=3 - f-состоянием и т.д. Электроны, находящиеся в этих состояниях, называются соответственно s-, p-, d-, f- и т.д. электронами. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях с n=2 и l=0 и l=1 обозначаются соответственно символами 2sи 2p. На рисунке 3.4 показана форма электронных облаков и их ориентация для s и p электронов. Распределения плотностей для s-электронов обладают сферической симметрией, тогда как для p-, d-, f-электронов они имеют выраженные направленные области концентрации электронной плотности. Согласно принципу Паули, в одном и том же атоме, не может быть более одного электрона с одинаковым набором четырех квантовых чисел. Поэтому максимальное число электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно С 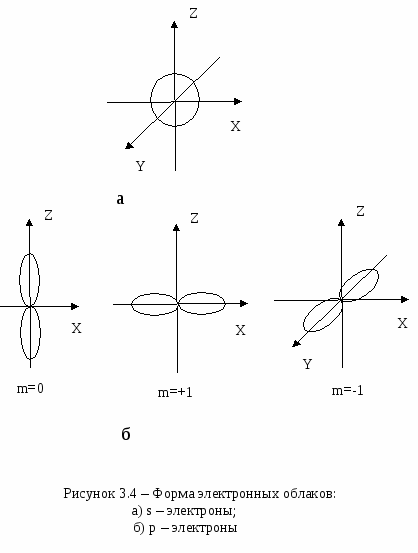 овокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой оболочке электроны распределяются по подоболочкам, соответствующим данному l. Поскольку орбитальное квантовое число принимает значения от 0 до n-1, число подоболочек равно порядковому номеру nоболочки. Количество электронов в подоболочке определяется магнитным и спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2l+1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в таблице 3.1. Таблица 3.1- Обозначения оболочек и распределение электронов по оболочкам и подоболочкам
Все уровни s являются невырожденными. Это означает, что каждому из них отвечает единственное состояние электрона в атоме. В соответствии с принципом Паули в таком состоянии могут находиться два электрона, отличающиеся друг от друга направлением своих спинов. Уровни p являются трехкратно вырожденными: каждому из них отвечает не одно, а три состояния, отличающееся друг от друга магнитным квантовым числом ml. При l=1 оно может принимать следующие три значения: ml= -1;0;+1. Так как в каждом состоянии может находиться два электрона, то для полного комплектования уровня p требуется 6 электронов. Уровни d имеют пятикратное вырождение, так как при l=2 магнитное квантовое число ml может принимать следующие пять значений: ml= -2; -1; 0;+1;+2. На этом уровне может разместиться 10 электронов. В общем случае уровень с орбитальным квантовым числом lимеет 2l+1 - кратное вырождение и на нем может разместиться 2(2l+1) электронов. 3.2 Периодическая система элементов Менделеева Принцип Паули, лежащий в основе систематики заполнения электронных состояний в атомах, позволяет объяснить Периодическую систему элементов Д. И. Менделеева (1869) - фундаментальный закон природы, являющегося основой современной химии, атомной и ядерной физики (см. таблицу 3.2). Таблица 3.2 - Систематика заполнения электронных состояний в атомах
Д. И. Менделеев ввел понятие порядкового номера Zхимического элемента, равного числу протонов в ядре и соответственно общему числу электронов в электронной оболочке атома. Расположив химические элементы по мере возрастания порядковых номеров, он получил периодичность в изменении химических свойств элементов. Однако для известных в то время 64 химических элементов некоторые клетки таблицы оказались незаполненными, так как соответствующие им элементы (например, Gа, Se, Gе) тогда еще не были известны. Д. И. Менделеев, таким образом, не только правильно расположил известные элементы, но и предсказал существование новых, еще не открытых, элементов и их основные свойства. Кроме того, Д. И. Менделееву удалось уточнить атомные веса некоторых элементов. Например, атомные веса Ве и U, вычисленные на основе таблицы Менделеева, оказались правильными, а полученные ранее экспериментально - ошибочными. Так как химические и некоторые физические свойства элементов объясняются внешними (валентными) электронами в атомах, то периодичность свойств химических элементов должна быть связана с определенной периодичностью в расположении электронов в атомах. Поэтому для объяснения таблицы будем считать, что каждый последующий элемент образован из предыдущего прибавлением к ядру одного протона и соответственно прибавлением одного электрона в электронной оболочке атома. Взаимодействием электронов пренебрегаем, внося, где это необходимо, соответствующие поправки. Рассмотрим атомы химических элементов, находящиеся в основном состоянии. Единственный электрон атома водорода находится в состоянии 1s, характеризуемом квантовыми числами n=1, l = 0, ml = 0 и ms= ± ½ (ориентация его спина произвольна). Оба электрона атома Не находятся в состоянии 1s, но с антипараллельной ориентацией спина. Электронная конфигурация для атома Не записывается как 1s2 (два 1s-электрона). На атоме Не заканчивается заполнение К-оболочки, что соответствует завершению I периода Периодической системы элементов Менделеева (см. таблицу 3.2). Третий электрон атома Li (Z=3), согласно принципу Паули, уже не может разместиться в целиком заполненной K-оболочке и занимает низшее энергетическое состояние с n=2 (L-оболочка), т. е. 2s-состояние. Электронная конфигурация для атома Li: 1s22s. Атомом Li начинается II период Периодической системы элементов. Четвертым электроном Ве (Z = 4) заканчивается заполнение подоболочки 2s. У следующих шести элементов от В (Z=5)до Nе (Z=10) идет заполнение подоболочки 2р. II период Периодической системы заканчивается неоном - инертным газом, для которого подоболочка 2р полностью заполнена. Одиннадцатый электрон Na (Z=11) размещается в М-оболочке (n=3), занимая низшее состояние 3s. Электронная конфигурация имеет вид 1s22s22р63s. 3s-электрон (как и 2s-электрон Li) является валентным электроном, поэтому оптические свойства Na подобны свойствам Li. С Z=12 идет последовательное заполнение М-оболочки. Аr (Z=18) оказывается подобным Не и Ne: в его наружной оболочке все s- и р-состояния заполнены. Аr является химически инертным и завершает III период Периодической системы. Девятнадцатый электрон К (Z=19) должен был бы занять 3d-состояние в М-оболочке. Однако и в оптическом, и в химическом отношениях атом К схож с атомами Li и Nа, которые имеют внешний валентный электрон в s-состоянии. Поэтому 19-й валентный электрон К должен также находиться в s-состоянии, но это может быть только s-состояние новой оболочки (N-оболочки), т.е. заполнение N-оболочки для К начинается при незаполненной М-оболочке. Это означает, что в результате взаимодействия электронов состояние n = 4, l = 0 имеет меньшую энергию, чем состояние n = 3, l = 2. Спектроскопические и химические свойства Са (Z=20) показывают, что его 20-й электрон также находится в 4s-состоянии N-оболочки. В последующих элементах происходит заполнение М-оболочки (от Sс (Z=21) до Zn (Z=30)). Далее N-оболочка заполняется до Кr (Z=36), у которого опять-таки, как и в случае Nе и Аr, s- и р-состояния наружной оболочки заполнены полностью. Криптоном заканчивается IV период Периодической системы. Подобные рассуждения применимы и к остальным элементам таблицы Менделеева, однако эти данные можно найти в справочниках. Отметим лишь, что и начальные элементы последующих периодов Rb, Сs, Fr являются щелочными металлами, а их последний электрон находится в s-состоянии. Кроме того, атомы инертных газов (Не, Nе, Аr, Кr, Хе, Rn) занимают в таблице особое положение - в каждом из них s- и р-состояния наружной оболочки полностью заполнены, и ими завершаются очередные периоды Периодической системы. Каждую из двух групп элементов - лантаниды (от лантана (Z=57) до лютеция (Z=71)) и актиниды (от актиния (Z=89) до лоуренсия (Z=103)) - приходится помещать в одну клетку таблицы, так как химические свойства элементов в пределах этих групп очень близки. Это объясняется тем, что для лантанидов заполнение подоболочки 4f, которая может содержать 14 электронов, начинается лишь после того, как полностью заполнятся подоболочки 5s, 5р и 6s. Поэтому для этих элементов внешняя Р-оболочка (6s2) оказывается одинаковой. Аналогично, одинаковой для актинидов является Q-оболочка (7s2). Таким образом, открытая Менделеевым периодичность в химических свойствах элементов объясняется повторяемостью в структуре внешних оболочек у атомов родственных элементов. Так, инертные газы имеют одинаковые внешние оболочки из 8 электронов (заполненные s- и р-состояния); во внешней оболочке щелочных металлов (Li, Na, К, Rb, Сs, Fr) имеется лишь один s-электрон; во внешней оболочке щелочно-земельных металлов (Ве, Мg, Са, Sr, Ва, Rа) имеется два s-электрона; галоиды (F, Сl, Вr, I, Аt) имеют внешние оболочки, в которых недостает одного электрона до оболочки инертного газа, и т. д. Лекция 4 Классификация кристаллов по типом связи 4.1 Силы, действующие между частицами твердого тела 4.2 Ионные кристаллы 4.3 Атомные кристаллы 4.4 Металлические кристаллы 4.5 Молекулярные кристаллы 4.6 Кристаллы с водородными связями 4.7 Сопоставление различных типов связей Классификация кристаллов по кристаллическим системам дает представление о геометрических характеристиках кристалла, но не затрагивает вопроса о природе сил, удерживающих атомы (молекулы или ионы) в определенных местах друг относительно друга - в узлах кристаллической решетки. Можно произвести классификацию кристаллов по другому принципу, а именно: в зависимости от физической природы сил, действующих между частицами кристалла. Тогда мы получим четыре типа кристаллов (кристаллических решеток): ионные, атомные, металлические и молекулярные. Классификация кристаллов, основанная на типах сил связи, позволяет сделать некоторые обобщения относительно свойств и поведения кристаллов, чего нельзя сделать, рассматривая только геометрию решеток. 4.1 Силы, действующие между частицами твердого тела До сих пор мы не учитывали природу сил, удерживающих частицы в строго упорядоченном положении. На самом деле необходимо учитывать природу этих сил, так как она определяет энергию связи в решетке и основные ее свойства. Рассмотрим силы взаимодействия и соответственно энергию связи для 2-х частичной модели (см. рисунок 4.1). 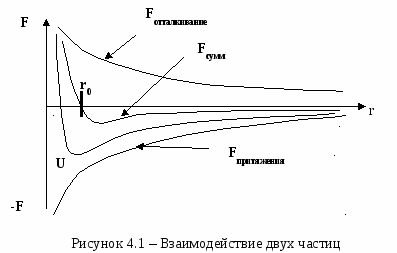 Пусть мы имеем две частицы одна, из которых расположена в начале координат, а вторая расположена в бесконечности и из бесконечности приближается к первой частице. Сила притяжения обычно описывается следующей формулой: где b и m - постоянные целые числа и зависят от природы решетки. По мере сближения частиц при малых r резко возрастает сила отталкивания. Обычно полагают где a и n целые постоянные числа, зависящие от типа решетки. Для того чтобы силы отталкивания при малых расстояниях между частицами превышали силу притяжения, необходимо чтобы n>m (для некоторых кристаллов полагают n=12, m=6). Тогда суммарную силу взаимодействия можно представить в виде: Зная, что можно показать, что суммарная потенциальная энергия взаимодействия системы 2-х частиц U определяется формулой: где | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
