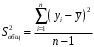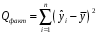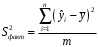Исследование операций и методы оптимизации
 Скачать 2.46 Mb. Скачать 2.46 Mb.
|
|
Министерство сельского хозяйства Российской Федерации Департамент образования, научно-технологической политики и рыбохозяйственного комплекса Федеральное государственное бюджетное образовательное учреждение высшего образования Волгоградский государственный аграрный университет О.А. Заяц ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ ОПТИМИЗАЦИИ Часть 2 Учебное пособие Волгоград Волгоградский ГАУ  1 КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ1.1 Парная регрессияВ зависимости от количества факторов, включенных в уравнение регрессии, различают парную и множественную регрессию. Парная регрессия представляет собой регрессию между двумя переменными – 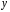 и и 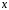 , т. е. модель вида: , т. е. модель вида: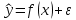 , ,где 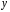 – зависимая переменная (объясняемая переменная, результативный признак); – зависимая переменная (объясняемая переменная, результативный признак);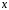 – независимая переменная (объясняющая переменная, факторный признак). – независимая переменная (объясняющая переменная, факторный признак).Знак «^» означает, что между переменными 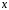 и и 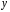 нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина 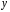 складывается из двух слагаемых: складывается из двух слагаемых: , ,где 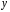 – фактическое значение результативного признака; – фактическое значение результативного признака; – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; – теоретическое значение результативного признака, найденное исходя из уравнения регрессии;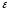 – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического: – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического: . (1.1) . (1.1)Случайная величина 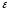 включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных. включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.К ошибкам спецификации относятся неправильный выбор той или иной математической функции для  и недоучет в уравнении регрессии какого-либо существенного фактора. и недоучет в уравнении регрессии какого-либо существенного фактора.В парной регрессии выбор вида математической функции 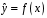 может быть осуществлен тремя методами: графическим; аналитическим, т.е. исходя из теории изучаемой взаимосвязи; экспериментальным. может быть осуществлен тремя методами: графическим; аналитическим, т.е. исходя из теории изучаемой взаимосвязи; экспериментальным.Графический метод подбора вида уравнения регрессии основан на поле корреляции. Поле корреляции – это поле точек, на котором каждая точка соответствует единице совокупности; ее координаты определяются значениями признаков x и y. По характеру расположения точек на поле корреляции делают вывод о наличии или отсутствии связи, о характере связи. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 1.1:  Линейная Парабола второй степени  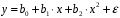 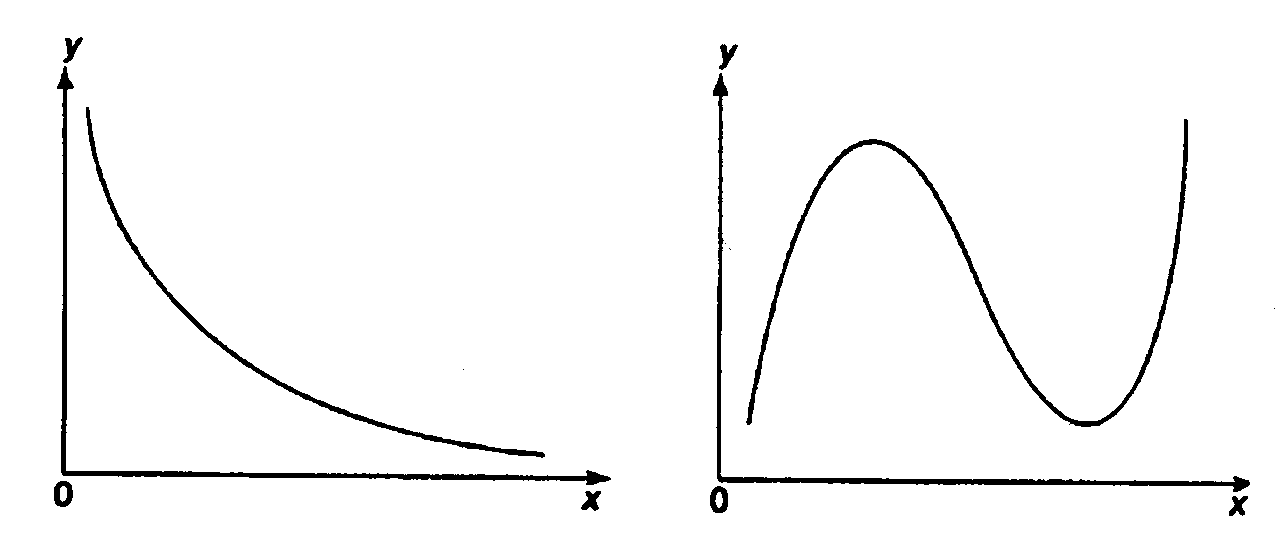 Равносторонняя гипербола Полином третьей степени 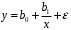 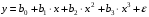  Степенная Показательная 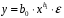 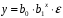 Рисунок 1.1 - Основные типы кривых, используемых при количественной оценке связей между двумя переменными Если линия регрессии 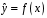 проходит через все точки корреляционного поля, что возможно только при функциональной связи, то проходит через все точки корреляционного поля, что возможно только при функциональной связи, то 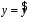 . В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Иными словами, имеют место отклонения фактических значений результативного признака от теоретических. Величина этих отклонений лежит в основе расчета остаточной дисперсии: . В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Иными словами, имеют место отклонения фактических значений результативного признака от теоретических. Величина этих отклонений лежит в основе расчета остаточной дисперсии: . (1.2) . (1.2)Чем меньше величина остаточной дисперсии, тем лучше уравнение регрессии подходит к исходным данным. Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной 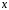 , т.е. если вид функции усложняется, то требуется увеличение объема наблюдений. , т.е. если вид функции усложняется, то требуется увеличение объема наблюдений.Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида: 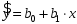 . (1.3) . (1.3)Построение линейной регрессии сводится к оценке ее параметров – 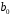 и и 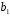 . . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 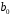 и и 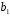 , при которых сумма квадратов отклонений фактических значений результативного признака , при которых сумма квадратов отклонений фактических значений результативного признака 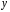 от теоретических от теоретических  минимальна: минимальна: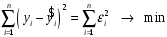 . (1.4) . (1.4)Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2). В выражение (1.4) подставим вместо 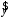 правую часть уравнения (1.3) и обозначим: правую часть уравнения (1.3) и обозначим:  . .   εi Рисунок 1.2 - Линия регрессии с минимальной дисперсией остатков Как известно из курса математического анализа, чтобы найти минимум функции (1.4), надо вычислить частные производные по каждому из параметров ( 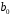 и и 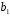 ) и приравнять их к нулю: ) и приравнять их к нулю: 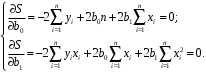 После преобразований, получим следующую систему линейных уравнений для оценки параметров 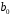 и и 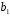 : : (1.5) (1.5)Решая систему уравнений (1.5), найдем искомые оценки параметров 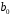 и и 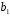 . Можно воспользоваться следующими формулами, которые следуют непосредственно из решения системы (1.5): . Можно воспользоваться следующими формулами, которые следуют непосредственно из решения системы (1.5):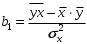 , (1.6) , (1.6) , (1.7) , (1.7)где 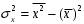 – дисперсия признака – дисперсия признака 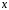 ; (1.8) ; (1.8) , , 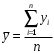 , ,  , ,  . .Параметр 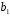 называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии показывает направление связи: при b1 > 0, связь прямая, а при b1 < 0 – связь обратная. Формально параметр b0 – это значение называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Знак при коэффициенте регрессии показывает направление связи: при b1 > 0, связь прямая, а при b1 < 0 – связь обратная. Формально параметр b0 – это значение 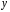 при при  . Если признак-фактор . Если признак-фактор 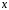 не может иметь нулевого значения, то вышеуказанная трактовка свободного члена b0 не имеет смысла, т.е. параметр b0 может не иметь экономического содержания. Попытки экономически интерпретировать параметр b0 могут привести к абсурду, особенно при b0 < 0. не может иметь нулевого значения, то вышеуказанная трактовка свободного члена b0 не имеет смысла, т.е. параметр b0 может не иметь экономического содержания. Попытки экономически интерпретировать параметр b0 могут привести к абсурду, особенно при b0 < 0. Для оценки тесноты линейной связи между двумя признаками рассчитывают линейный коэффициент парной корреляции  : :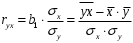 , (1.9) , (1.9)где 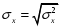 - среднее квадратическое отклонение признака х; - среднее квадратическое отклонение признака х;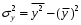 - дисперсия признака y; (1.10) - дисперсия признака y; (1.10)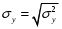 - среднее квадратическое отклонение признака y. - среднее квадратическое отклонение признака y.Среднее квадратическое отклонение показывает на сколько в среднем величина изучаемого признака у отдельных единиц совокупности отличается от среднего значения признака в совокупности. Линейный коэффициент парной корреляции находится в пределах: 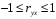 . Чем ближе абсолютное значение . Чем ближе абсолютное значение  к единице, тем сильнее линейная связь между признаками, чем ближе значение к единице, тем сильнее линейная связь между признаками, чем ближе значение  к нулю, тем слабее связь. При к нулю, тем слабее связь. При 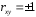 имеем строгую функциональную зависимость. Если имеем строгую функциональную зависимость. Если 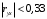 , линейная связь между y и x слабая; если , линейная связь между y и x слабая; если 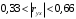 , линейная связь между y и xсредняя; если , линейная связь между y и xсредняя; если 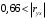 , линейная связь между y и x тесная. , линейная связь между y и x тесная.Близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной. Для оценки качества подбора функции рассчитывается коэффициент детерминации, характеризующий долю дисперсии результативного признака 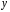 , объясняемую регрессией, в общей дисперсии результативного признака: , объясняемую регрессией, в общей дисперсии результативного признака: . (1.11) . (1.11)Величина 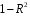 характеризует долю дисперсии характеризует долю дисперсии 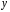 , вызванную влиянием остальных не учтенных в модели факторов. , вызванную влиянием остальных не учтенных в модели факторов.Линейный коэффициент детерминации может быть рассчитан как квадрат линейного коэффициента корреляции: 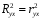 . .Чтобы иметь общее суждение о точности модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации: 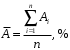 . (1.12) . (1.12)где 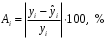 - индивидуальная ошибка аппроксимации. - индивидуальная ошибка аппроксимации.Если 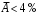 - модель отличного качества; если - модель отличного качества; если  - модель хорошего качества; если - модель хорошего качества; если  - удовлетворительная модель; если - удовлетворительная модель; если  - необходимо строить другую модель. - необходимо строить другую модель.Оценка значимости уравнения регрессии в целом производится на основе 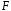 -критерия Фишера, которому предшествует дисперсионный анализ. -критерия Фишера, которому предшествует дисперсионный анализ. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной 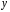 от среднего значения от среднего значения  раскладывается на две части – «объясненную» и «необъясненную»: раскладывается на две части – «объясненную» и «необъясненную»: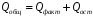 , ,где Qобщ – общая сумма квадратов отклонений; Qфакт – факторная сумма квадратов отклонений (сумма квадратов отклонений, объясненная регрессией); Qост – остаточная сумма квадратов отклонений. Любая сумма квадратов отклонений связана с числом степеней свободы df, т. е. с числом свободы независимого варьирования признака. Схема дисперсионного анализа имеет вид, представленный в таблице 1.1 ( 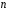 – число наблюдений, – число наблюдений, 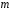 – число параметров при независимых переменных). – число параметров при независимых переменных).Таблица 1.1 – Дисперсионный анализ
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину 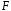 -критерия Фишера: -критерия Фишера: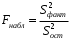 . (1.13) . (1.13)Оценивание качества модели по F-критерию Фишера состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого наблюдаемое значение 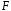 -критерия Фишера (1.13) сравнивается с критическим (табличным) значением -критерия Фишера (1.13) сравнивается с критическим (табличным) значением 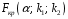 при уровне значимости при уровне значимости 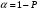 и степенях свободы и степенях свободы 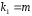 и и 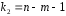 (Приложение 1). (Приложение 1). Если Fнабл > Fкр, то гипотеза H0 отклоняется и признается статистическая значимость и надежность уравнения регрессии и показателя тесноты связи. Если Fнабл < Fкр, то гипотеза H0 не отклоняется и признается статистическая незначимость и ненадежность уравнения регрессии и показателя тесноты связи. Величина 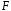 -критерия связана с коэффициентом детерминации -критерия связана с коэффициентом детерминации 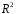 , и ее можно рассчитать по следующей формуле: , и ее можно рассчитать по следующей формуле: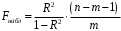 . (1.14) . (1.14)Для оценки статистической значимости параметров уравнения регрессии применяется t-распределение Стьюдента. Величина параметра сравнивается с его стандартной ошибкой, т.е. определяется наблюдаемое (фактическое) значение 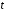 -критерия Стьюдента: -критерия Стьюдента: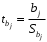 , (1.15) , (1.15)которое сравнивается с критическим (табличным) значением 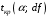 при уровне значимости при уровне значимости 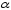 и числе степеней свободы и числе степеней свободы 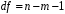 (Приложение 2). (Приложение 2). Стандартные ошибки параметров линейной регрессии определяются по формулам: 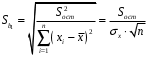 , (1.16) , (1.16)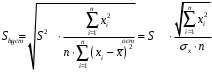 . (1.17) . (1.17)где 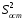 – остаточная дисперсия на одну степень свободы. – остаточная дисперсия на одну степень свободы.Если | 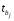 | > tкр, то параметр bj признается статистически значимым. Если | | > tкр, то параметр bj признается статистически значимым. Если |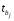 | < tкр, то признается статистическая незначимость параметра bj. | < tкр, то признается статистическая незначимость параметра bj.Величина стандартной ошибки совместно с 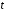 -распределением Стьюдента применяется для расчета доверительного интервала параметров регрессии. Доверительным интервалом называется такой интервал, относительно которого можно с заранее выбранной вероятностью P утверждать, что он содержит значения прогнозируемого показателя. -распределением Стьюдента применяется для расчета доверительного интервала параметров регрессии. Доверительным интервалом называется такой интервал, относительно которого можно с заранее выбранной вероятностью P утверждать, что он содержит значения прогнозируемого показателя.Доверительный интервал для параметров уравнения регрессии определяется как:  . (1.18) . (1.18)Границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, 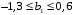 . .В прогнозных расчетах по уравнению регрессии определяется предсказываемое 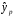 значение как точечный прогноз значение как точечный прогноз  при при 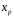 , т.е. путем подстановки в уравнение регрессии , т.е. путем подстановки в уравнение регрессии 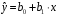 соответствующего значения соответствующего значения 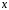 . Однако точечный прогноз явно нереален, поэтому он дополняется интервальной оценкой прогнозного значения . Однако точечный прогноз явно нереален, поэтому он дополняется интервальной оценкой прогнозного значения 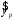 : :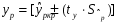 , (1.19) , (1.19)где  – средняя ошибка прогнозируемого индивидуального значения y: – средняя ошибка прогнозируемого индивидуального значения y: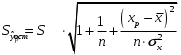 . (1.20) . (1.20) |