Исследование операций и методы оптимизации
 Скачать 2.46 Mb. Скачать 2.46 Mb.
|
1.5 Множественная регрессияПарная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии 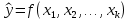 , (2.1) , (2.1)где y – зависимая переменная (результативный признак); xj – независимые, или объясняющие, переменные (признаки-факторы). Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели: отбора факторов и выбора вида уравнения регрессии. Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: - быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность; - не должны быть коррелированы между собой и тем более находиться в точной функциональной связи. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 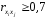 . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F-критерий меньше табличного значения. Возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной множественной регрессии 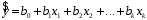 . (2.2) . (2.2)Параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне. Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). Система линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (2.2) имеет вид: 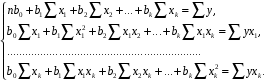 (2.3) (2.3)Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи коэффициент множественной корреляции может быть найден по формуле:  , (2.4) , (2.4)где 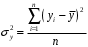 или или 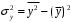 – общая дисперсия результативного признака; – общая дисперсия результативного признака; 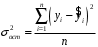 – остаточная дисперсия. – остаточная дисперсия.Границы изменения коэффициента множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Коэффициент детерминации: 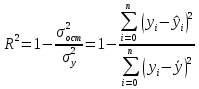 . (2.5) . (2.5)Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера: 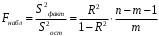 . (2.11) . (2.11)Наблюдаемые значения t-критерия Стьюдента можно определить по формуле: 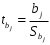 , (2.14) , (2.14)где bj – коэффициент чистой регрессии при факторе xj; 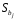 –стандартная ошибка коэффициента регрессии bj. –стандартная ошибка коэффициента регрессии bj.Стандартная ошибка коэффициента регрессии: 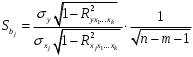 , (2.15) , (2.15)где 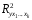 – коэффициент детерминации для уравнения множественной регрессии; – коэффициент детерминации для уравнения множественной регрессии; 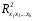 – коэффициент детерминации для зависимости фактора – коэффициент детерминации для зависимости фактора 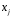 со всеми другими факторами уравнения множественной регрессии. со всеми другими факторами уравнения множественной регрессии.Прогнозирование по модели множественной регрессии проводится аналогично прогнозированию по уравнению парной регрессии. Точечный прогноз –расчетное значение результата, полученное подстановкой в уравнение регрессии прогнозных значений факторов: 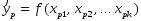 . (2.16) . (2.16)Интервальный прогноз для линейной функции: 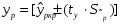 . (2.17) . (2.17)Средняя ошибка прогнозного значения результата: 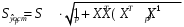 , (2.18) , (2.18)где  – матрица исходных значений факторов; – матрица исходных значений факторов;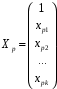 - матрица-столбец прогнозных значений факторов; - матрица-столбец прогнозных значений факторов;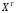 - транспонированная матрица; - транспонированная матрица;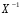 - обратная матрица. - обратная матрица.Прогнозирование по нелинейным моделям множественной регрессии также можно осуществлять по формулам (2.16), (2.17), (2.18), предварительно линеаризовав указанные модели. |
