Исследование операций и методы оптимизации
 Скачать 2.46 Mb. Скачать 2.46 Mb.
|
1.3 Нелинейная регрессияЕсли между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например: – полиномы разных степеней 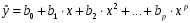 ; (1.21) ; (1.21)– равносторонняя гипербола – 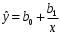 ; (1.22) ; (1.22)– полулогарифмическая функция – 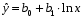 . (1.23) . (1.23)2. Регрессии, нелинейные по оцениваемым параметрам, например: – степенная – 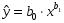 ; (1.24) ; (1.24)– показательная – 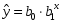 ; (1.25) ; (1.25)– экспоненциальная – 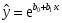 ; (1.26) ; (1.26)– логистическая 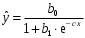 ; (1.27) ; (1.27) – обратная 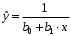 . (1.28) . (1.28)Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Например, парабола второй степени 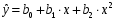 приводится к линейному виду с помощью замены: приводится к линейному виду с помощью замены: 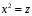 . В результате приходим к двухфакторному уравнению . В результате приходим к двухфакторному уравнению 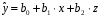 , оценка параметров которого при помощи МНК приводит системе уравнений: , оценка параметров которого при помощи МНК приводит системе уравнений: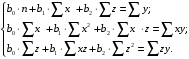 (1.29) (1.29)Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. Равносторонняя гипербола 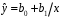 может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y. может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы y. Равносторонняя гипербола и полулогарифмическая кривая используются для описания кривой Энгеля (математическое описание взаимосвязи доли расходов на товары длительного пользования и общих сумм расходов (или доходов)). Уравнения, в которых входят 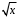 , применяются в исследованиях урожайности, трудоемкости сельскохозяйственного производства. , применяются в исследованиях урожайности, трудоемкости сельскохозяйственного производства.Регрессии, нелинейные по оцениваемым параметрам, делятся на два типа: внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и внутренне нелинейные (к линейному виду не приводятся). К внутренне линейным моделям относятся, например, степенная, показательная, экспоненциальная, логистическая, обратная функции. Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры. Степенная функция используется, например, при изучении эластичности спроса от цены. Широкое использование степенной функции связано с тем, что параметр 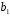 в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. Коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. Коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Для оценки тесноты нелинейной связи рассчитывают: 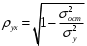 , (1.30) , (1.30)где 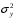 – общая дисперсия результативного признака – общая дисперсия результативного признака 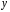 ; ;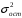 – остаточная дисперсия. – остаточная дисперсия.Величина данного показателя находится в пределах: 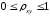 . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.Индекс детерминации характеризует долю дисперсии результативного признака 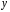 , объясняемую регрессией, в общей дисперсии результативного признака, определяется как: , объясняемую регрессией, в общей дисперсии результативного признака, определяется как: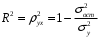 . (1.31) . (1.31)Качество нелинейного уравнения регрессии можно оценить с помощью средней ошибки аппроксимации 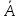 , F-критерия Фишера и t-критерия Стьюдента. , F-критерия Фишера и t-критерия Стьюдента.ПРИМЕР 2. По регионам России известны данные о среднедушевых денежных доходах населения (х) и потребительских расходах в среднем на душу населения (у) за 2019 г. (Приложение 4). Требуется: 1. Для характеристики зависимости y от x построить уравнение степенной регрессии. 2. Оценить тесноту связи изучаемых признаков. Оценить качество уравнения регрессии через среднюю ошибку аппроксимации и F-критерий Фишера. Решение: 1. При построении уравнения регрессии для выбора вида математической функции используется графический метод. Предположим, что зависимость между доходами и расходами нелинейная. Для подтверждения нашего предположения построим поле корреляции (рис. 1.2). По графику видно, что точки выстраиваются в линию, похожую на график степенной функции. Построению нелинейной модели предшествует процедура линеаризации переменных. Линеаризация степенной модели 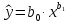 (1.33) (1.33)производится путем логарифмирования обеих частей уравнения: 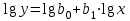 . .Введем замену: z=lgy,v=lgx, В=lgb0, тогда 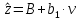 . (1.34) . (1.34)Для расчетов используем данные z и v (рис. 1.10). 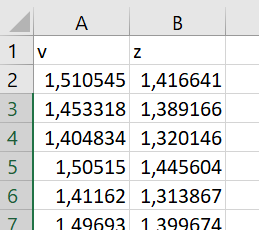 Рисунок 1.10 Выделите любой диапазон ячеек размерностью 5х2, нажмите кнопку 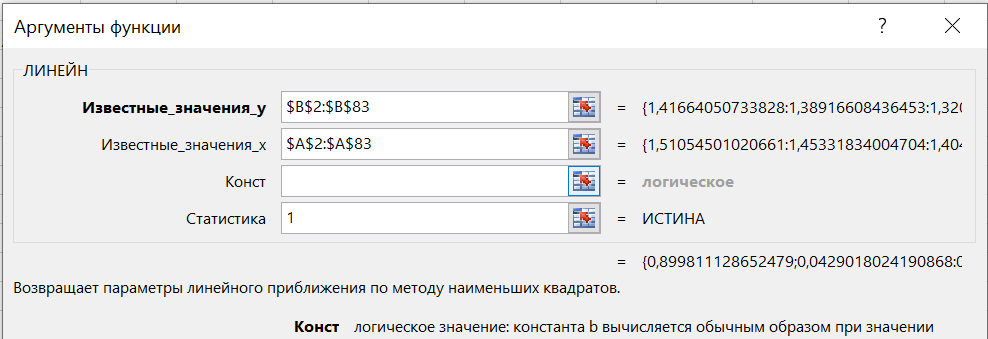 Рисунок 1.11 – Ввод аргументов Для ввода формулы нажмите одновременно Ctrl+Shift+Enter (не ОК!). Если уже нажали ОК, вызовите режим редактирования формулы (например, клавишей F2) и нажмите Ctrl+Shift+Enter. Округлите полученные значения с помощью кнопок 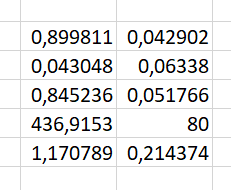 Рисунок 1.12 – Результат применения функции ЛИНЕЙН Получим линейное уравнение: 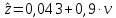 . (1.35) . (1.35)Путем обратных преобразований уравнения (1.35) (lgb0 = B, b0 = 10B =100,043 = 1,104), получаем степенное уравнение регрессии: 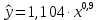 . (1.36) . (1.36)С увеличением среднедушевых денежных доходов на 1 % потребительские расходы в среднем на душу населения увеличиваются в среднем на 0,9 %. 2. Подставляя в уравнение (1.36) фактические значения факторного признака xi,получаем теоретические значения результативного признака 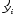 . По ним рассчитаем индекс корреляции . По ним рассчитаем индекс корреляции 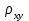 =0,87 и среднюю ошибку аппроксимации =0,87 и среднюю ошибку аппроксимации  =8%. Степенная зависимость урожайности зерновых культур от дозы внесения удобрений тесная. Ошибка аппроксимации показывает хорошее соответствие расчетных и фактических данных. Так как Fнабл > Fкр (240 > 3,96), уравнение регрессии (1.36) признается статистически значимым и надежным. =8%. Степенная зависимость урожайности зерновых культур от дозы внесения удобрений тесная. Ошибка аппроксимации показывает хорошее соответствие расчетных и фактических данных. Так как Fнабл > Fкр (240 > 3,96), уравнение регрессии (1.36) признается статистически значимым и надежным. |
