Исследование операций и методы оптимизации

• Название: Исследование операций и методы оптимизации
• Дата: 01.06.2022
• Размер: 2.46 Mb.
• Имя файла: IO_i_MO_chast_2.docx
• Тип: Исследование; #563610
• страница: 2 из 13

1.2 Решение задач корреляционно-регрессионного анализа в Excel с помощью встроенных функций

ПРИМЕР 1. По регионам России известны данные о среднедушевых денежных доходах населения (х) и потребительских расходах в среднем на душу населения (у) за 2019 г. (Приложение 4).

Требуется:

1. Рассчитать числовые характеристики изучаемых признаков.

2. Оценить тесноту связи изучаемых признаков.

3. Построить уравнение парной линейной регрессии y от x.

4. Оценить статистическую значимость уравнения регрессии в целом с помощью F-критерий Фишера и параметров регрессии с помощью t-критерия Стьюдента при уровне значимости 0,05.

5. Оценить качество уравнения регрессии через среднюю ошибку аппроксимации.

6. Дать точечный и интервальный прогноз расходов с вероятностью 0,9, принимая уровень дохода равным 110% от среднего уровня.

Решение: Предположим, что связь между доходами и расходами линейная (рис. 1.2).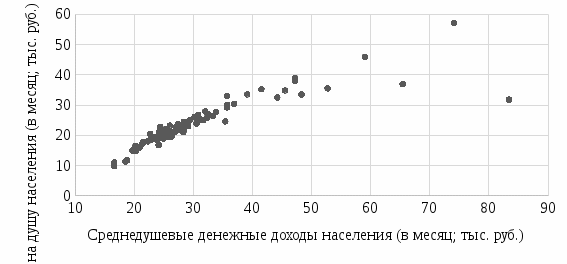



Рисунок 1.2 – Поле корреляции

1. Расчет числовых характеристик (среднее значение, среднее квадратическое отклонение, дисперсия):

1) введите исходные данные в ячейки листа Excel в соответствии с рис. 1.3.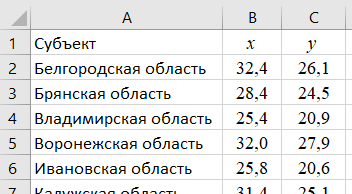



Рисунок 1.3 – Исходные данные

2) числовые характеристики определим с помощью статистических функций СРЗНАЧ (среднее значение), СТАНДОТКЛОН.Г (среднее квадратическое отклонение), ДИСП.Г (дисперсия). Вычисления выполните в любых свободных ячейках (рис. 1.4).



Рисунок 1.4 – Отображение формул в режиме «Показать формулы»

Дисперсия по ряду х: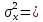

135,60.

Среднее квадратическое отклонение по ряду х: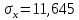

– в среднем среднедушевые денежные доходы населения отклоняются от среднего по регионам дохода на 11,645 тыс. руб.

Дисперсия по ряду у: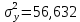

.

Среднее квадратическое отклонение по ряду у:

- в среднем потребительские расходы населения отклоняются от средних по регионам расходов на 7,525 тыс. руб.

Примечание: Для характеристики однородности совокупности используется коэффициент вариации V. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для близких к нормальному распределений). Если V < 10%, то вариация данных слабая, если 10% <V< 20% - средняя, если V > 20% - сильная.

- вариация признака х сильная.

- вариация признака у сильная.

Так как Vх> 33% совокупность данных по доходам неоднородна. Для однородности данных необходимо исключить аномальные наблюдения (г. Москва – 74 тыс. руб. и Чукотский АО – 83 тыс. руб.). В данном примере оставим совокупность данных без изменений, но при выполнении научных исследований, по результатам которых планируется опубликование статьи, рекомендуется строить модели по однородным данным.

2. Расчет парного линейного коэффициента корреляции:

1) выделите любую ячейку, нажмите кнопку и вставьте функцию КОРРЕЛ (категория Статистические);

2) введите аргументы функции (рис. 1.5), нажмите ОК.



Рисунок 1.5 – Ввод аргументов функции КОРРЕЛ

Линейный коэффициент парной корреляции:

r_yx=0,876.

Линейная связь между признаками у и х тесная, прямая.

3. Определение параметров уравнения регрессии (и не только!):

1) выделите любой диапазон ячеек размерностью 5х2 (например, E2:F6), нажмите кнопку 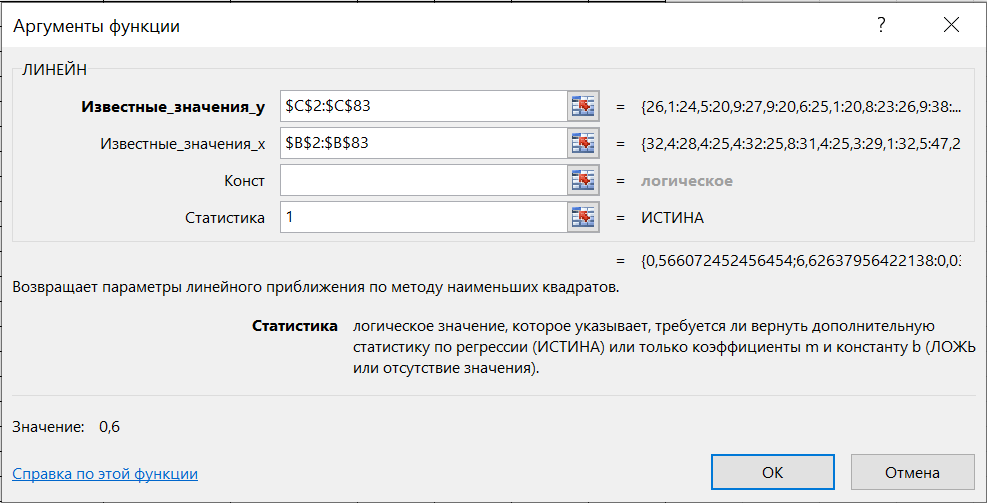и вставьте функцию ЛИНЕЙН (категория Статистические), введите аргументы функции, при этом сразу после ввода каждого диапазона в поля «Известные_значения_у» и «Известные_значения_х» нажмите клавишу F4 для получения абсолютных ссылок (рис. 1.6);



Рисунок 1.6 – Ввод аргументов функции ЛИНЕЙН

2) для ввода формулы нажмите одновременно Ctrl+Shift+Enter (не ОК!). Если уже нажали ОК, вызовите режим редактирования формулы (например, клавишей F2) и нажмите Ctrl+Shift+Enter. Округлите полученные значения с помощью кнопок до нужного количества знаков после запятой (рис. 1.7);


k₂ и df

S_ост



F_набл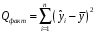



R²





b₀

b₁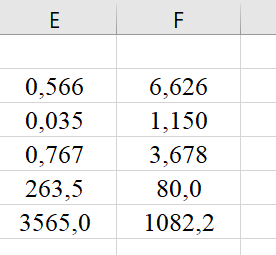


Рисунок 1.7 – Результат применения функции ЛИНЕЙН

3) в результате функция ЛИНЕЙН выводит: в первой строке 1 - оценки параметров модели, во второй - стандартные ошибки, в третьей - коэффициент детерминации и стандартную ошибку регрессии, в четвертой - значение F-статистики и число степеней свободы, в пятой - факторную и остаточную суммы квадратов отклонений.
Уравнение парной линейной регрессии имеет вид:

. (*)

С увеличением среднедушевых денежных доходов на 1 тыс. руб. потребительские расходы в среднем на душу населения увеличиваются в среднем на 0,566 тыс. руб. в месяц.

Коэффициент детерминации: .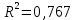

Вариация результатана 76,7% объясняется вариацией фактора x. На долю прочих факторов, не учитываемых в уравнении регрессии, приходится 23,3 %.

4. Определение критических значений F-критерия Фишера и t-критерия Стьюдента:

1) критическое значение F-критерия найдем с помощью статистической функции F.ОБР(1-;k₁;k₂) при уровне значимости α=0,05 и степенях свободы k₁=m=1 (m – число параметров при независимой переменной в уравнении регрессии) и k₂=n-m-1=82-1-1=80 (рис. 1.8):

F_кр(0,05;1;80) = 3,96.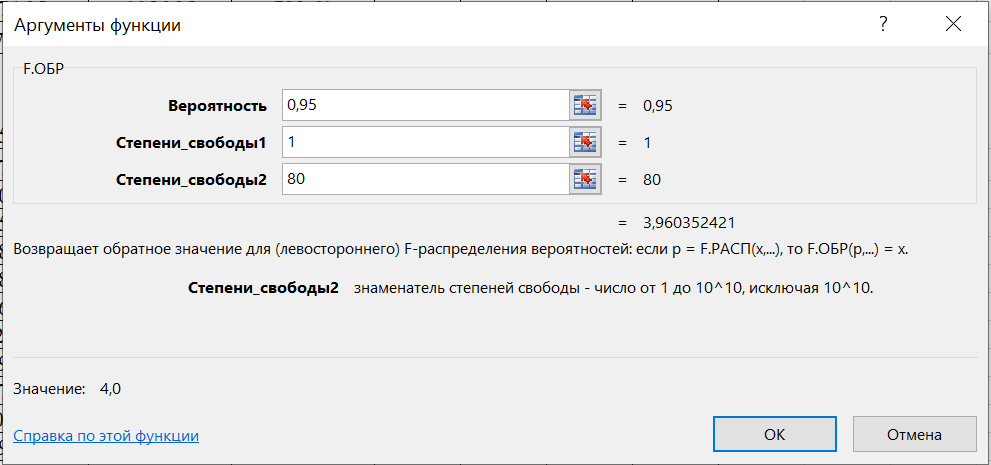



Рисунок 1.8 – Определение F_кр

Для оценки статистической значимости уравнения регрессии в целом сравним наблюдаемое значение F-критерия Фишера (рис. 1.7) с критическим.

Так какF_набл> F_кр (263 > 3,96), с вероятностью 0,95 уравнение регрессии в целом признается статистически значимым и надежным.

2) критическое значение t-критерия найдем с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х(;df) при уровне значимости α=0,05 и степенях свободы df=n-m-1=82-1-1=80 (рис. 1.9):

t_кр(0,05;80) = 1,99.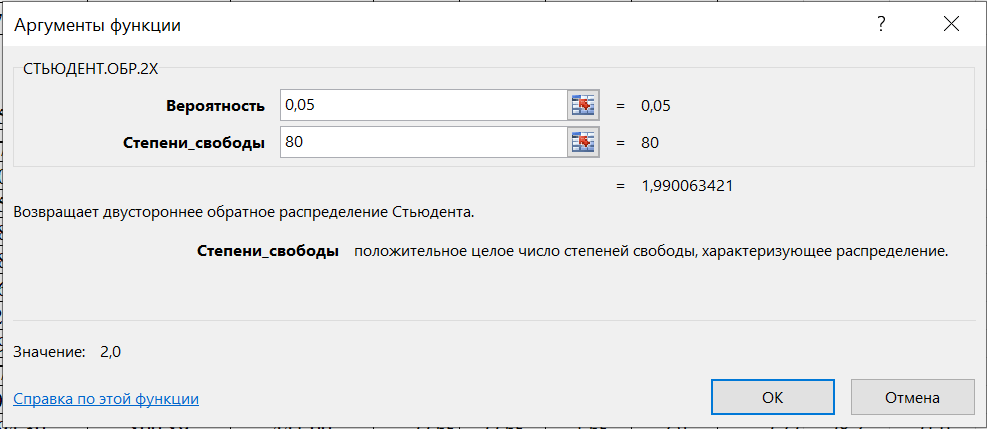



Рисунок 1.9 – Определение t_кр

Оценку статистической значимости параметров уравнения регрессии проведем с помощью t-критерия Стьюдента и путем расчета доверительного интервала каждого из показателей.

Стандартные ошибки параметров уравнения регрессии (рис. 1.7).

Наблюдаемые значения t-критерия Стьюдента: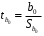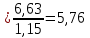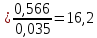

; .

Так как и больше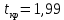 , параметрыb₀ и b₁статистически значимы.

Рассчитаем доверительный интервал параметров b₀ и b₁: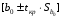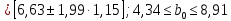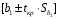

.

.

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 0,95 параметры b₀ и b₁, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми.

5. Среднюю ошибку аппроксимации определим по формуле (1.12). Расчетные значения результативного признака найдем, подставляя в уравнение (*) значения факторного признака x_i: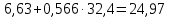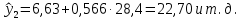

= ,



Рассчитаем индивидуальные ошибки аппроксимации по одной из формул: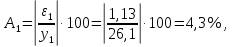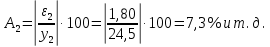

.





Средняя ошибка аппроксимации: .

Ошибка аппроксимации показывает удовлетворительное соответствие расчетных и фактических данных: среднее отклонение составляет 10%.

Примечание. Низкая точность модели в данном случае может быть следствием неоднородности исходных данных по признаку х (так, если исключить из выборки всего два аномальных наблюдения, средняя ошибка аппроксимации составит 7,4%).

6. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Точечный прогноз потребительских расходов при прогнозном значении среднедушевых доходов населения х_р=1,130,85=33,935≈34 тыс. руб. составит: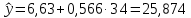

тыс. руб.

Чтобы получить интервальный прогноз, найдем среднюю ошибку прогноза по формуле (1.20) (S_ост см. рис. 1.7):

.

Критическое значение t-критерия для уровня значимости α=0,1 и числа степеней свободы df=82-1-1=80: t_кр(0,1;80)=1,66.

Доверительный интервал прогнозируемых расходов: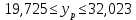

.

.

При среднедушевых денежных доходах населения, равных 34 тыс. руб., потребительские расходы в среднем на душу населения с вероятностью 0,9 составят от 19,7 до 32,0 тыс. руб. в месяц.