Исследование операций и методы оптимизации
 Скачать 2.46 Mb. Скачать 2.46 Mb.
|
1.6 Решение задач корреляционно-регрессионного анализа в Excel с помощью инструментов анализа данных КОРРЕЛЯЦИЯ и РЕГРЕССИЯПРИМЕР 1. Изучается влияние на валовой региональный продукт (у, млн. руб.) различных факторов: стоимости основных фондов (х1, млн. руб.), объема инновационных товаров (х2, млн. руб.), фонда начисленной заработной платы работников (х3, млн. руб.) (приложение 5, данные за 2018 г.). Требуется: 1. На основе матрицы парных коэффициентов корреляции выполнить отбор факторов, включаемых в регрессию. 2. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров. 3. Определить множественный коэффициент корреляции и детерминации. 4. С вероятностью 0,99 оценить статистическую значимость уравнения множественной регрессии с помощью F-критерия Фишера. 5. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов при переменных х1 и х2 множественного уравнения регрессии при уровне значимости 0,01. 6. Оценить качество уравнения регрессии через среднюю ошибку аппроксимации. 7. Найти прогноз валового регионального продукта при стоимости основных фондов (х2) 126397352 млн. руб. и объеме инновационных товаров (работ, услуг) 1425670 млн. руб. Решение: 1. Матрицу парных коэффициентов корреляции переменных определим, используя инструмент анализа данных Корреляция: 1) запишите данные в ячейки листа Excel(рис. 2.1); 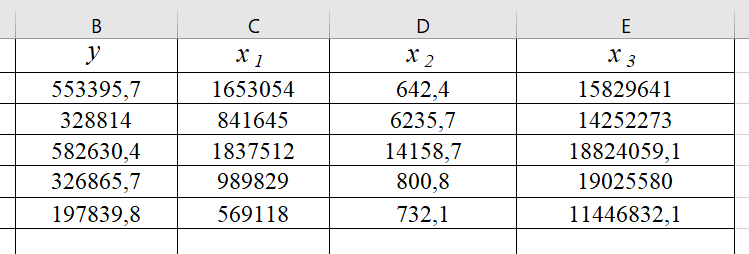 Рисунок 2.1 – Исходные данные 2) выберете Данные/Анализ данных/Корреляция. Щелкните по кнопке ОК; 3) заполните диалоговое окно ввода данных и параметров вывода «Корреляция» (рис. 2.2);  Рисунок 2.2 - Диалоговое окно «Корреляция» 3) результаты вычислений представлены на рис. 2.3. 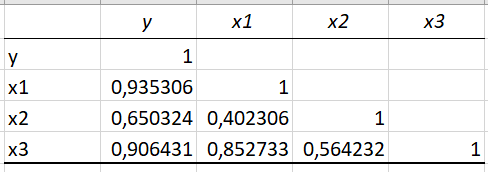 Рисунок 2.3 - Матрица коэффициентов парной корреляции Рассмотрим влияние каждого из факторов на результат:  Все факторы оказывают заметное влияние на результат. Наибольшее влияние оказывает фактор х1, наименьшее – фактор х2. Связь между факторами х1 и х2 – средняя  , х1 и х3 – тесная , х1 и х3 – тесная  , между факторами х2 и х3 – средняя , между факторами х2 и х3 – средняя . Так как . Так как 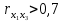 , факторы х1 и х3 коллинеарны. , факторы х1 и х3 коллинеарны. В модель регрессии должны быть включены факторы, тесно связанные с результатом и слабо связанные друг с другом. В данной задаче этим требованиям удовлетворяют две модели регрессии:  и и  . .Выбор конкретной модели зависит от целей исследования. Фактор х1 характеризует влияние фактора производства - капитал, а фактор х3 - фактора производства - труд. В данном примере влияние фактора х1незначительно, но сильнее, чем фактора х3, к тому же фактор х1 слабее связанс фактором х2. Далее будем рассматривать модель зависимости валового регионального продукта от стоимости основных фондов и объема инновационных товаров, работ, услуг: 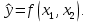 2. Линейное уравнение множественной регрессии y от x1 и x2: 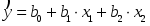 . (2.19) . (2.19)Рассчитаем параметры уравнения регрессии в MSExcel с помощью инструмента анализа данных Регрессия: 1) выберете Данные/Анализ данных/Регрессия. Щелкните по кнопке ОК; 2) заполните диалоговое окно ввода данных и параметров вывода «Регрессия» (рис. 2.4): Входной интервал Y – диапазон, содержащий данные результативного признака; Входной интервал Х – диапазон, содержащий данные факторов независимого признака; Метки – флажок, указывающий, содержит ли первая строка названия столбцов или нет; Уровень надежности - применяется для построения доверительных интервалов параметров регрессии (по умолчанию - 95%). Если флажок установлен, а уровень надежности отличен от 95%, то рассчитываются два доверительных интервала: для 95% и другого (введенного) уровня надежности; 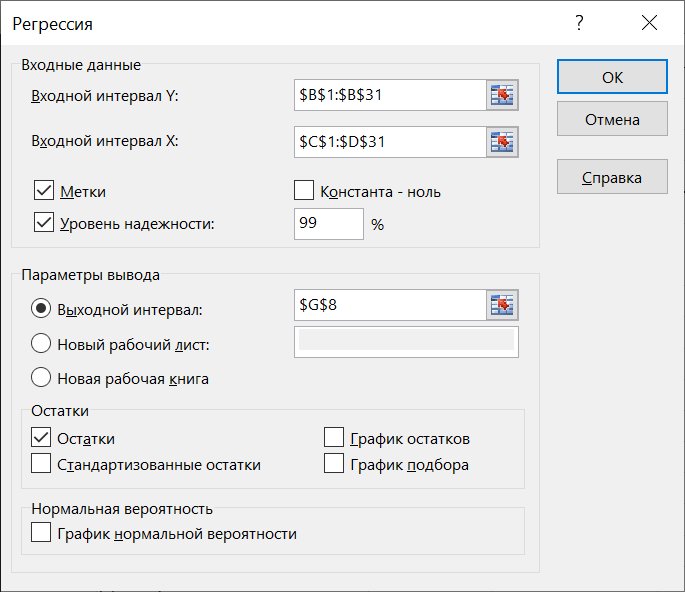 Рисунок 2.4 - Диалоговое окно «Регрессия» Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении; Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона; Остатки – флажок, позволяющий вывести таблицу расчетных значений зависимого признака 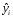 и остатков и остатков 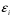 . .Щелкните по кнопке ОК. В результате применения инструмента Регрессия будет получено несколько таблиц (рис. 2.5). Столбец Коэффициенты третьей таблицы содержит численные значения параметров регрессии: b0=39646, b1=0,3038, b2=2,2072. Линейное уравнение множественной регрессии y от x1 и x2:  (2.20) (2.20)При увеличении стоимости основных фондов на 1 млн. руб. валовой региональный продукт увеличивается на 0,304 млн. руб. при неизменном объеме инновационных товаров (работ, услуг). При увеличении объема инновационных товаров (работ, услуг) на 1 млн. руб. валовой региональный продукт увеличивается на 2,207 млн. руб. при неизменной стоимости основных фондов. 3. Значение коэффициента множественной корреляции расположено в строке Множественный Rтаблицы Регрессионная статистика (рис. 2.5):  Линейная зависимость валового регионального продукта от стоимости основных фондов и объема инновационных товаров (работ, услуг) тесная. Линейная зависимость валового регионального продукта от стоимости основных фондов и объема инновационных товаров (работ, услуг) тесная.Множественный коэффициент детерминации (строка R-квадрат табл. Регрессионная статистика, рис. 2.5): R2=0,964. Вариация объема выпуска продукции на 96,4 % определяется вариацией учтенных в регрессии (2.20) факторов. 4. В таблице Дисперсионный анализ (рис. 2.5) представлены результаты многофакторного дисперсионного анализа. Столбец SS содержит суммы квадратов отклонений; столбец MS – дисперсии в расчете на одну степень свободы; столбец F – наблюдаемое значение F-критерия Фишера: Fнабл=366. Критическое значение F-критерия найдем с помощью статистической функции F.ОБР(1-;k1;k2) при уровне значимости  и степенях свободы и степенях свободы  и и 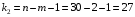 (в поле Вероятность вводим 0,99 (1-α или 1-0,01)): (в поле Вероятность вводим 0,99 (1-α или 1-0,01)): 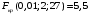 . .Так как Fнабл > Fкр,с вероятностью 0,99 уравнение регрессии (2.20) признается статистически значимым и надежным.  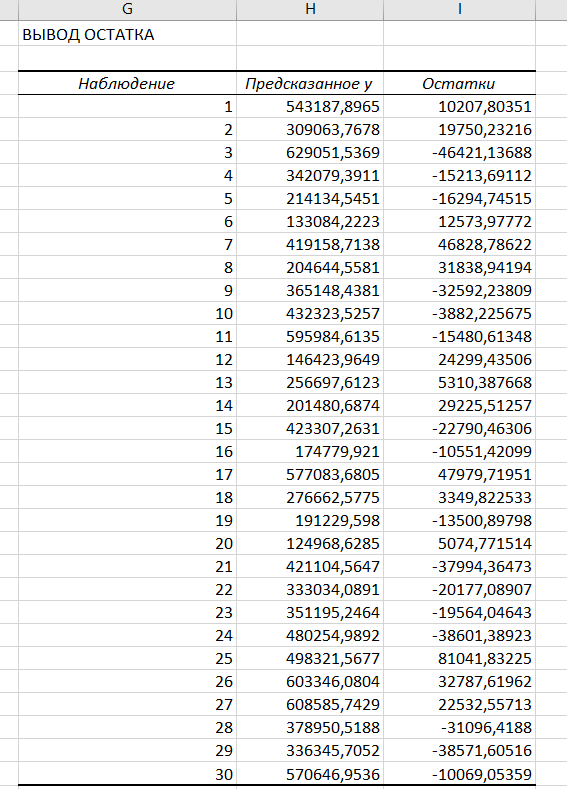 Рисунок 2.5 - Результат применения инструмента Регрессия 5. Значения стандартных ошибок и наблюдаемые значения t-критерия Стьюдента для параметров регрессии расположены в третьей таблице вывода итогов построения регрессии (рис. 2.5) в столбцах «Стандартная ошибка» и «t-статистика», соответственно:  . .Критическое значение t-критерия найдем с помощью статистической функции СТЬЮДЕНТ.ОБР.2Х для уровня значимости 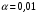 и степени свободы и степени свободы  : :  . . Так как,  и и  больше больше 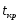 , коэффициенты регрессии b1 и b2 являются статистически значимыми и надежными. , коэффициенты регрессии b1 и b2 являются статистически значимыми и надежными. Примечание. При незначимости параметра b0, принято оставлять константу в уравнении регрессии для поглощения влияния неучтенных в модели факторов. В данном примере параметр уравнения b0 статистически значим. 6. Рассчитаем индивидуальные ошибки аппроксимации:  , используя данные таблицы Вывод остатка (рис. 2.5). , используя данные таблицы Вывод остатка (рис. 2.5).Столбец Предсказанное у содержит расчетные (теоретические) значения результативного признака (объема выпуска продукции)  , столбец Остатки – значения остатков модели , столбец Остатки – значения остатков модели  : :   Рисунок 2.6 – Ввод формулы расчета ошибки аппроксимации  … … …  Рисунок 2.7 – Результат расчета средней ошибки аппроксимации Уравнение регрессии (2.20) хорошего качества (  ). ).7. Точечный прогноз валового регионального продукта составит:  Ошибку прогноза определим по формуле (2.18): 1) введите матрицы Х и X p (рис. 2.8), единичный столбец вводится для учета присутствия константы в уравнении регрессии; 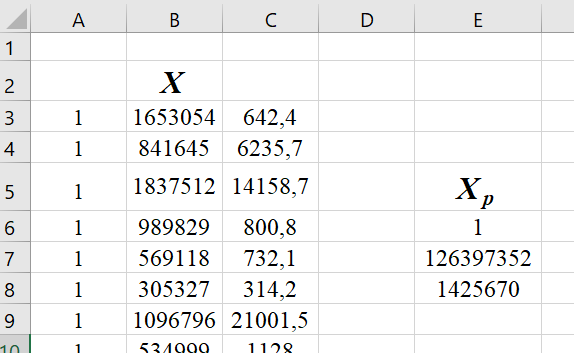 Рисунок 2.8 – Ввод матриц Х и Х р 2) с помощью кнопки Транспонировать(А) 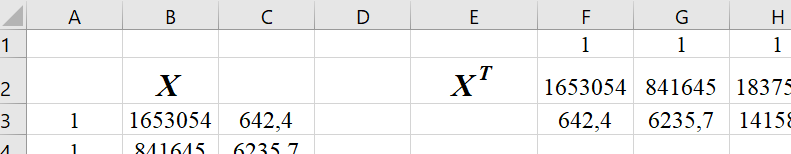 Рисунок 2.9 – Ввод матрицы ХT 3) найдите произведение матриц Х Tи Х с помощью функции МУМНОЖ (категория Математические). Примечание. Произведение матриц возможно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В, т.е. A(m;n) на B(n;r) (в результате будет получена матрица C(m;r)). Для вычисления результата: - выделите диапазон ячеек размерности m×r (m - количество строк первой матрицы, r– количество столбцов второй матрицы); - вызовите функцию МУМНОЖ и заполните поля аргументов (рис. 2.10, а); - завершите ввод формулы комбинацией клавиш Ctrl + Shift + Enter (! не ОК). Примечание. Если нажали ОК раньше, чем комбинацию клавиш, выделите диапазон ячеек заново (левая верхняя ячейка будет уже рассчитана, а остальные пустые), вызовите режим редактирования формулы (клавишей F2) и нажмите Ctrl+Shift+Enter (рис. 2.10, б); 4) найдите обратную матрицу (Х TХ)-1с помощью функции МОБР (категория Математические). Для вычисления результата: - выделите диапазон ячеек такой же размерности, что и исходная матрица (Х TХ); - вызовите функцию МОБР и заполните поля аргументов (рис. 2.11, а); - завершите ввод формулы комбинацией клавиш Ctrl + Shift + Enter (рис. 2.11, б), результат получен в экспоненциальной форме (можно перевести в числовой);  а  б Рисунок 2.10 – Вычисление произведения матриц  а  б Рисунок 2.11 – Вычисление обратной матрицы Примечание. Найти обратную матрицу можно только при условии, что исходная является квадратной (количество столбцов и строк одинаковое). К тому же, ее определитель не должен равняться цифре 0. 5) найдите матрицу ХрТ (транспонируйте матрицу Хр) (рис. 2.12); 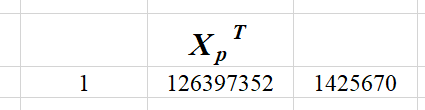 Рисунок 2.12 - Ввод матрицы Хр T 6) найдите произведение матриц ХрТ и(Х TХ)-1 (диапазон выделяется размерностью 1×3, так как в первой матрице одна строка, а во второй три столбца)(рис. 2.13); 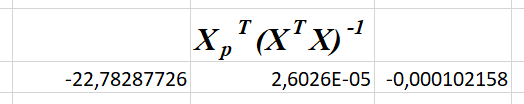 Рисунок 2.13 – Вычисление произведения матриц 7) найдите произведение матриц ХрТ(Х TХ)-1иХр (диапазон выделяется размерностью 1×1, так как в первой матрице одна строка, а во второй один столбец)(рис. 2.14); 8)Sост = 31554 - рис. 2.5, табл. Регрессионная статистика строка Стандартная ошибка. 9) ошибка прогноза: 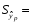 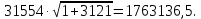 Табличное значение t-критерия: 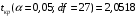 . .Интервальный прогноз:  Таким образом, с вероятностью 0,95 можно утверждать, что если стоимость основных фондов составит 126397352 млн. руб., а объем инновационных товаров (работ, услуг) 1425670 млн. руб. то валовой региональный продукт будет находиться в пределах от 37967 млрд. руб. до 45203 млрд. руб. |
